神经网络

让我们研究一下如何用神经网络表示一个假设函数。在一个非常简单的层次上，神经元基本上是计算单元，它把输入（树突）作为电输入（称为“尖峰”），引导到输出（轴突）。在我们的模型中，我们的树突就像输入特征X1⋯xn，而输出则是我们的假设函数的结果。在这个模型中我们X0输入节点有时被称为“偏差”。它总是等于1。在神经网络中，我们使用与分类相同的逻辑函数，然而，我们有时称之为逻辑（logistic）激活函数。在这种情况下，我们的“θ”参数有时称为“权重”。

视觉上，一个简单的表示看起来像：

我们的输入节点（第1层），也称为“输入层”，进入另一个节点（第2层），最后输出假设函数，称为“输出层”。

我们可以在输入层和输出层之间设置中间层，称为“隐藏层”。

在这个例子中，我们把这些中间或隐藏层节点，称他们为“激活单位。”

=在第j层的激活

=从层j到层j＋1控制函数映射的权重矩阵

如果我们有一个隐藏层，它看起来像：

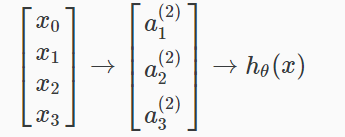
每个“激活”节点的值如下所获得：

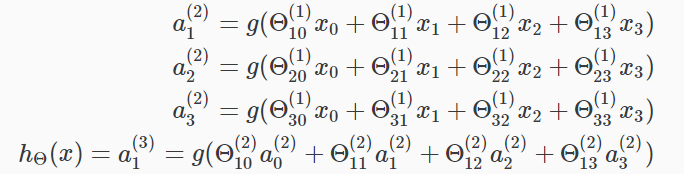
这是说我们计算我们的激活节点采用3×4矩阵参数。我们将参数的每一行应用到我们的输入中，以获得一个激活节点的值。我们假设输出为逻辑函数应用到我们的激活节点的值的总和，它已乘以另一个参数矩阵Θ（2）含量的第二层节点。

每一层都有自己的矩阵的权重，Θ^(j)。

这些权重矩阵的尺寸如下所示：

如果网络有S_j节点在J层和有S_j+1节点在J+1层，然后Θ^(j)将变成s_j+1*（s_j+1）。

示例：第1层有2个输入节点，第2层有4个激活节点。维Θ（1）将4×3 SJ = 2 + 1 = 4，SJ，SJ 1×（SJ + 1）= 4×3。