A Simple Problem with Integers---poj3468线段树

http://poj.org/problem?id=3468

 

题意：有一个比较长的区间可能是100000.长度， 每个点都有一个值（值还比较大），

现在有一些操作：

C a b c， 把区间a--b内全部加上c

Q a b，求区间ab的值和。

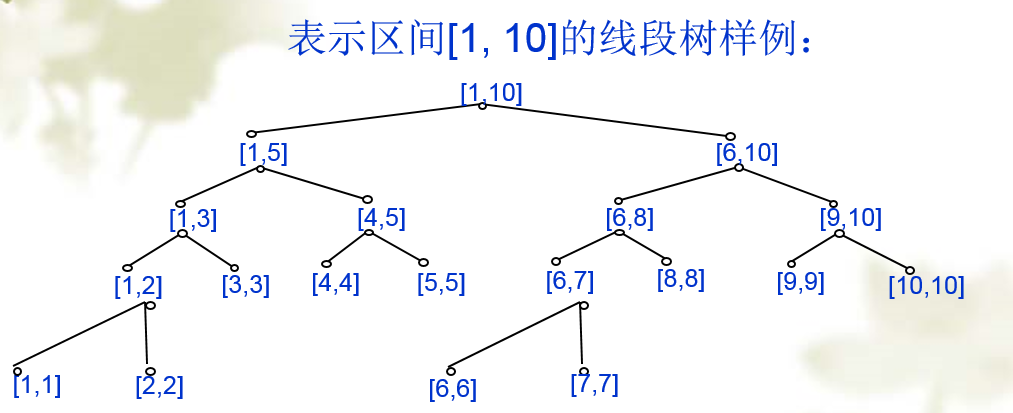
线段树 改变整个区间的数

这题不能直接更新到树的叶子节点， 因为那样时间复杂度太高，我们可以在每个节点上加一个变量k，表示这个节点的所有点（L到R）都要增加 k, 所以我们可以在从上往下查找的过程中如果不是所求区间，那么我们就把本区间加上应该加的数，否则的话，就停止，这样每次更新的过程时间复杂度也是log n，查找时， 我们需要把含有K值得那些点放到它的子节点上去，只需要一层就可以了，具体过程看代码

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;

#define INF 0xfffffff
#define N 400050
#define Lson root<<1
#define Rson root<<1|1

struct SegmentTree
{
    int L, R;
    long long sum, k;
    int Mid()
    {
        return (L+R)>>1;
    }
    int len()
    {
        return R-L+1;
    }
} a[N<<2];

void BuildSegTree(int root, int L, int R)
{
    a[root].L = L;
    a[root].R = R;
    a[root].k = 0;
    if( L == R )
    {
        scanf("%lld", &a[root].sum);
        return ;
    }

    BuildSegTree(Lson, L, a[root].Mid());
    BuildSegTree(Rson, a[root].Mid()+1, R);

    a[root].sum = a[Rson].sum + a[Lson].sum;
}

void Update(int root, int L, int R, int k)
{
    a[root].sum += (R - L + 1) * k;

    if(a[root].L == L && a[root].R == R)///当到达要更新的那个区间时，把k值更新，并返回；
    {
        a[root].k += k;
        return ;
    }

    if(R <= a[root].Mid())///右边；
        Update(Lson, L, R, k);
    else if(L > a[root].Mid())///左边；
        Update(Rson, L, R, k);
    else///中间；
    {
        Update(Lson, L, a[root].Mid(), k);
        Update(Rson, a[root].Mid()+1, R, k);
    }
}

void Down(int root)
{
    a[Lson].sum += a[Lson].len()*a[root].k;
    a[Rson].sum += a[Rson].len()*a[root].k;///左右儿子的和都要增加对应的值，注意这里看清楚增加的是谁；
    a[Lson].k += a[root].k;
    a[Rson].k += a[root].k;///接着往下传递K值；
    a[root].k = 0;///传下去之后就置0；
}
long long Query(int root, int L, int R)
{
    if(a[root].L==L && a[root].R == R)///当刚好是这个区间时返回结果；
        return a[root].sum;

    Down(root);///往下传递K值；

    if(R <= a[root].Mid())
        return Query(Lson, L, R);
    else if( L > a[root].Mid())
        return Query(Rson, L, R);
    else
    {
        long long Lsum = Query(Lson, L, a[root].Mid());
        long long Rsum = Query(Rson, a[root].Mid()+1, R);
        return Lsum + Rsum;
    }
}

int main()
{
    int n, m, L, R, k;
    long long ans;
    char s[10];
    while(scanf("%d %d", &n, &m) != EOF)
    {
        BuildSegTree(1, 1, n);
        for(int i=0; i<m; i++)
        {
            scanf("%s", s);
            if(s[0] == 'Q')
            {
                scanf("%d %d", &L, &R);
                ans = Query(1, L, R);
                printf("%lld
", ans);
            }
            else
            {
                scanf("%d %d %d", &L, &R, &k);
                Update(1, L, R, k);
            }
        }
    }
    return 0;
}
/*
100
2 3 4 5 6 7 8 9 10
Q 1 5
C 1 10 1
Q 3 5

*/