Vasya is studying in the last class of school and soon he will take exams. He decided to study polynomials. Polynomial is a function P(x) = a0 + a1x1 + ... + anxn. Numbers ai are called coefficients of a polynomial, non-negative integer n is called a degree of a polynomial.
Vasya has made a bet with his friends that he can solve any problem with polynomials. They suggested him the problem: "Determine how many polynomials P(x) exist with integer non-negative coefficients so that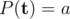 
, and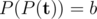 
, where 
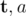and b are given positive integers"?
Vasya does not like losing bets, but he has no idea how to solve this task, so please help him to solve the problem.
The input contains three integer positive numbers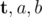 
no greater than 1018.
If there is an infinite number of such polynomials, then print "inf" without quotes, otherwise print the reminder of an answer modulo 109 + 7.
2 2 2
2
2 3 3
1
这题是机智题啊。。。
相当于是在问有多少个数在t进制下表示是a，在a进制表示下是b
结论是当t=a=b=1的时候有无数解，t=a=b!=1的时候两解，其他情况只有最多一解
p(t)=a,说明多项式系数之和<=a，等于a的情况只有t==1的时候，这个可以特判，所以可以认为处理完之后系数之和<a
然后因为p(a)=b，把b在a进制下展开，各个位数之和<a，因为p(t)=a限制了系数之和<a
如果b在a进制下表示为一个数x，想要调整x的位数得到其他解是行不通的
因为对于x的某一位，只能通过这一位-1，下一位+a的方式在保证不违背p(a)=b的情况下调整
这样系数和加上了a-1。原来系数和p>=1，现在p+a-1>=a，这跟前面的系数和<a矛盾，所以最多一解。得到p(a)=b的解了还要验证下p(t)=a是否成立。
这题细节超多各种特判，比如a==1的时候b在a进制表示不出啥的
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<queue> 8 #include<deque> 9 #include<set> 10 #include<map> 11 #include<ctime> 12 #define LL long long 13 #define inf 0x7ffffff 14 #define pa pair<int,int> 15 #define mkp(a,b) make_pair(a,b) 16 #define pi 3.1415926535897932384626433832795028841971 17 using namespace std; 18 inline LL read() 19 { 20 LL x=0,f=1;char ch=getchar(); 21 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 22 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 23 return x*f; 24 } 25 LL d[110],len; 26 LL t,a,b; 27 int main() 28 { 29 t=read();a=read();b=read(); 30 if (t==a&&a==b) 31 { 32 if (a==1)puts("inf"); 33 else puts("2"); 34 return 0; 35 } 36 if (t==1) 37 { 38 if (a==1)puts("0"); 39 else 40 { 41 LL tot=0,mxx=0,mul=1; 42 while (b) 43 { 44 d[++len]=b%a; 45 tot+=d[len]; 46 b/=a; 47 mxx+=mul*d[len]; 48 mul*=a; 49 } 50 if (tot<=a&&a-tot<=mxx&&(a-tot)%(a-1)==0)puts("1"); 51 else puts("0"); 52 } 53 return 0; 54 } 55 if (a==b){puts("1");return 0;} 56 LL _a=a; 57 while (_a) 58 { 59 d[++len]=_a%t; 60 _a/=t; 61 } 62 LL sum=0,mul=1; 63 for (int i=1;i<=len;i++) 64 { 65 sum+=d[i]*mul; 66 mul*=a; 67 } 68 if (sum==b)puts("1"); 69 else puts("0"); 70 }