算法导论学习

一、插入排序法：

解释：检查第i个数字，如果在它的左边的数字比它大，进行交换，这个动作一直继续下去，直到这个数字的左边数字比它还要小，就可以停止了。插入排序法主要的回圈有两个变数：i和j，每一次执行这个回圈，就会将第i个数字放到左边恰当的位置去。

性能：算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。

实现：使用python实现

def insertSort(lists):
    listLen = len(lists)
    for j in range(0,listLen):
        key = lists[j]
        i = j - 1
        while i >= 0 and lists[i] > key:
            lists[i+1] = lists[i]
            i = i - 1
        lists[i + 1] = key
    return lists
listsex = [1,5,4,3,7,9,10,3,2,6]
print(insertSort(listsex))
>>> 
[1, 2, 3, 3, 4, 5, 6, 7, 9, 10]
>>> 

二、归并排序法：

解释：该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

过程：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

性能：速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列，时间复杂度为O(n log n)。

实现：使用python实现

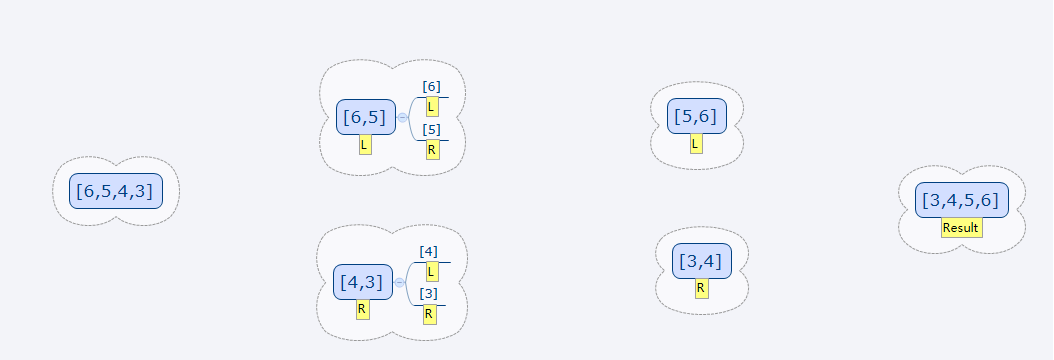
def MergeSort(lists):
    listLen = len(lists)
    if listLen <= 1:
        return lists
    num = int(listLen/2)
    print(num)
    print(listLen)
    print(lists)
    left = MergeSort(lists[:num])
    print(left)
    right = MergeSort(lists[num:])
    print(right)
    return Merge(left,right)
def Merge(left,right):
    r,l = 0,0
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += right[r:]
    result += left[l:]
    return result
    print(result)
listsex = [6,5,4,3]
print(MergeSort(listsex))
>>> 
2
4
[6, 5, 4, 3]
1
2
[6, 5]
[6]
[5]
[5, 6]
1
2
[4, 3]
[4]
[3]
[3, 4]
[3, 4, 5, 6]
>>> 

 递归过程：