新西兰数学奥林匹克总计3道题目, 考试时间为90分钟.
在 $ riangle{ABC}$ 三边外侧作 $ riangle{BPC}, riangle{QAC}, riangle{ARB}$. $angle{PBC} = angle{CAQ} = 45^circ$, $angle{BCP} = angle{QCA} = 30^circ$, $angle{ABR} = angle{BAR} = 15^circ$. 证明: $QRperp RP$, $QR = RP$.
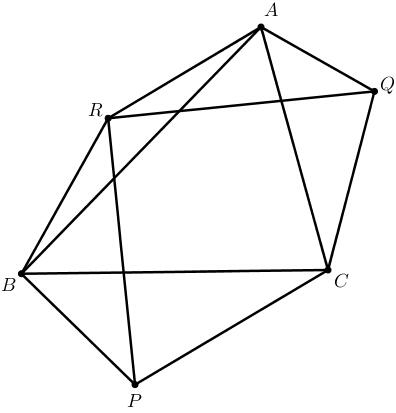
解答:
易知 $angle{ARB} = 180^circ - 30^circ = 150^circ$, 因此需要证明 $angle{ARQ} + angle{BRP} = 60^circ$.
由已知 $angle{PBC} = angle{CAQ} = 45^circ$ 及 $angle{ABR} = angle{BAR} = 15^circ$, 考虑将 $ riangle{ARQ}$ 及 $ riangle{BRP}$ 分别绕 $A, B$ 两点旋转在 $AB$ 外侧形成正三角形, 即以 $AB$ 为边作正三角形 $ABX$, 连结 $XR$, $XC$ (如下图所示).

此时需证明 $angle{ARQ} = angle{AXC}$ 及 $angle{BRP} = angle{BXC}$, 即需证明 $ riangle{ARQ}sim riangle{AXC}$ 及 $ riangle{BRP}sim riangle{BXC}$. 由于已知一角相等, 待证另一角相等, 因此考虑证明如下等式 $${ARover AX} = {AQover AC}, {BRover BX} = {BPover BC}.$$ 这可由 $ riangle{AXR} sim riangle{ACQ}$ ($AA$) 及 $ riangle{BXR}sim riangle{BCP}$ ($AA$) 分别证明之.
由 $ riangle{ARQ}sim riangle{AXC}$ 及 $ riangle{BRP}sim riangle{BXC}$ 可知, $${QRover XC} = {ARover AX} = {BR over BX} = {RP over XC}Rightarrow QR = RP.$$ Q.E.D.