排序算法总结

1. 冒泡排序

原理：比较两个相邻的元素，将值大的元素交换至右端。

思路：依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。重复第一趟步骤，直至全部排序完成。

/*
* 冒泡排序
*/
public class BubbleSort {
　　public static void main(String[] args) {
　　　　int[] arr={6,3,8,2,9,1};
　　　　System.out.println("排序前数组为：");
　　　　for(int num:arr){
　　　　　　System.out.print(num+" ");
　　　　}
　　　　for(int i=0;i<arr.length-1;i++){//外层循环控制排序趟数
　　　　　　for(int j=0;j<arr.length-1-i;j++){//内层循环控制每一趟排序多少次
　　　　　　　　if(arr[j]>arr[j+1]){
　　　　　　　　　　int temp=arr[j];
　　　　　　　　　　arr[j]=arr[j+1];
　　　　　　　　　　arr[j+1]=temp;
　　　　　　　　}
　　　　　　}
　　　　} 
　　　　System.out.println();
　　　　System.out.println("排序后的数组为：");
　　　　for(int num:arr){
　　　　　　System.out.print(num+" ");
　　　　} 
　　}
}

2.直接插入排序

从第一个数开始遍历，将每次遍历的数都插入到前面的有序数组中，（待插入值与前面的数比较，将大于temp的数后移，最后插入temp到 a[j+1]位置）

//直接插入排序
        for(int i=1;i<a.length;i++){
            int temp=a[i];//新遍历的值，等待插入前面已排好序的有序数组
            int j;
            //将大于temp的数后移
            for(j=i-1;j>=0;j--){
                if(a[j]>temp){
                    a[j+1]=a[j];
                }
                else{
                    break;
                }
            }
            a[j+1]=temp;
        }

3.二分插入排序

与直接插入排序原理一样，只是将查找插入位置变成二分查找方式

public static void main(String[] args){
         int[] a={34,12,3,22,78,1,98,66,55,44,7,3,1,0,-1};
         for(int i=1;i<a.length;i++){
             int temp=a[i];
             int left=0;
             int right=i-1; 
             //接下来二分查找比a【i】小的数的最右边位置
             while(left<=right){
                 int mid=(left+right)/2;
                 if(temp<=a[mid]){
                     right=mid-1;
                 }else{
                     left=mid+1;
                 }
             }
             //最后left就是要插入的位置left后到i-1的数据要后移
             for(int j=i-1;j>=left;j--){
                 a[j+1]=a[j];
             }
             //最后将a[i]插入到序列中
             a[left]=temp;
         }
         for(int val:a){
             System.out.println(val);
         }
    }

 4. 希尔排序（又称为增量排序）

是一种不稳定排序，思路：

 首先将待排序的一组数按某个增量分为若干子序列，并对子序列分别进行插入排序或者其他排序方式排序（以下代码是其他方式排序的）。
 然后逐渐将增量减小,并重复上述过程。直至增量为1，此时数据序列基本有序，最后进行一次插入排序。

public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a={49,1,8,79,65,34,22,19,7,40,80,89};
        int d=a.length;
        while(true){
            d=d/2;
            //分为d组数，需要对每组排序（采用以下排序方式），共d趟
            for(int i=0;i<d;i++){
                //组内排序
                //外层循环只是对小组内的数排序完所需要的趟数
                for(int j=i;j+d<a.length;j+=d){
                    //内循环两两比较，如需要则进行交换
                    for(int n=i;n+d<a.length;n+=d){
                        int temp;//前边大于后边，交换
                        if(a[n]>a[n+d]){
                            temp=a[n+d];
                            a[n+d]=a[n];
                            a[n]=temp;
                        }
                    }                    
                }
            }
            if(d==1){break;}
        
        }        
        for(int k=0;k<a.length;k++){
            System.out.println(a[k]);
        }
    }

//普通排序  希尔排序用到这个思想
    public static void main(String[] args){
        int[] a={8,5,7,2,10,9};
        int temp;
        for(int i=0;i<a.length-1;i++){
            for(int j=0;j<a.length-1;j++){
                if(a[j]>a[j+1]){
                    temp=a[j+1];
                    a[j+1]=a[j];
                    a[j]=temp;
                }
            }
        }
        for(int k=0;k<a.length;k++){
            System.out.println(a[k]);
        }        
    }

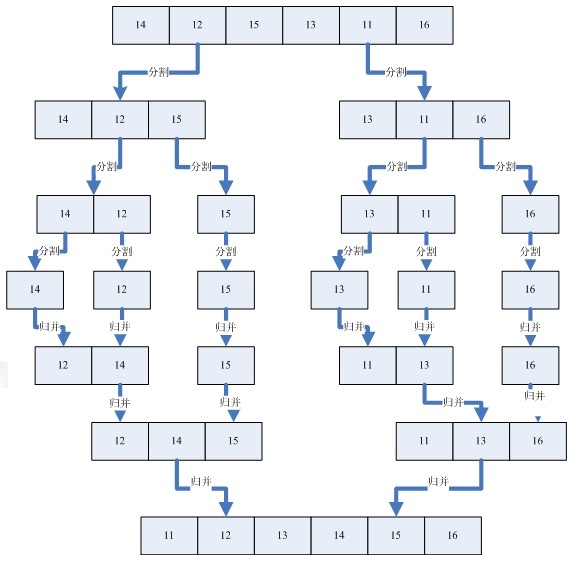
 5. 两路归并排序

算法思路:分而治之(divide - conquer);每个递归过程涉及三个步骤:

第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
第三, 合并: 合并两个排好序的子序列,生成排序结果.

public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a={49,1,8,79,65,34,22,19,7,40,80,89};
        int d=a.length;
        while(true){
            d=d/2;
            //分为d组数，需要对每组排序（采用以下排序方式），共d趟
            for(int i=0;i<d;i++){
                //组内排序
                //外层循环只是对小组内的数排序完所需要的趟数
                for(int j=i;j+d<a.length;j+=d){
                    //内循环两两比较，如需要则进行交换
                    for(int n=i;n+d<a.length;n+=d){
                        int temp;//前边大于后边，交换
                        if(a[n]>a[n+d]){
                            temp=a[n+d];
                            a[n+d]=a[n];
                            a[n]=temp;
                        }
                    }                    
                }
            }
            if(d==1){break;}
        
        }        
        for(int k=0;k<a.length;k++){
            System.out.println(a[k]);
        }
    }
//普通排序  希尔排序用到这个思想
    public static void main(String[] args){
        int[] a={8,5,7,2,10,9};
        int temp;
        for(int i=0;i<a.length-1;i++){
            for(int j=0;j<a.length-1;j++){
                if(a[j]>a[j+1]){
                    temp=a[j+1];
                    a[j+1]=a[j];
                    a[j]=temp;
                }
            }
        }
        for(int k=0;k<a.length;k++){
            System.out.println(a[k]);
        }        
    }
 5. 两路归并排序
算法思路:分而治之(divide - conquer);每个递归过程涉及三个步骤:

第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
第三, 合并: 合并两个排好序的子序列,生成排序结果.



public static int[] sort(int[] a,int low,int high){
        int mid = (low+high)/2;
        if(low<high){
            sort(a,low,mid);
            sort(a,mid+1,high);
            //左右归并
            merge(a,low,mid,high);
        }
        return a;
    }
     
    public static void merge(int[] a, int low, int mid, int high) {
        int[] temp = new int[high-low+1];
        int i= low;
        int j = mid+1;
        int k=0;
        // 把较小的数先移到新数组中
        while(i<=mid && j<=high){
            if(a[i]<a[j]){
                temp[k++] = a[i++];
            }else{
                temp[k++] = a[j++];
            }
        }
        // 把左边剩余的数移入数组 
        while(i<=mid){
            temp[k++] = a[i++];
        }
        // 把右边边剩余的数移入数组
        while(j<=high){
            temp[k++] = a[j++];
        }
        // 把新数组中的数覆盖nums数组
        for(int x=0;x<temp.length;x++){
            a[x+low] = temp[x];
        }
    }
 　　public static void main(String[] args) { 

 　　　　　int[] num = { 1, 5, 3, 2 };  

     　　 sort(num, 0, num.length - 1); 

 　　　　　for (int i = 0; i < num.length; i++)  

     　　　　　　System.out.print(num[i] + " ");  

  　 }