行列式

1、行列式

行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det(A)或 | A | 。无论是在线性代数、多项式理论，还是在微积分学中(比如说换元积分法中)，行列式作为基本的数学工具，都有着重要的应用。

引理：行列互换，值不变。

引理：用一个数乘行列式的某行等于用这个数乘此行列式。

引理：如果行列式中某一行是两组数之和，则这个行列式等于两个行列式之和，这两个行列式分别以这两组数为该行，而其余各行与原行列式对应各行相同。

引理：对换行列式中两行的位置，行列式反号。

引理：如果行列式中有两行成比例，则行列式等于0。

引理：把一行的某个倍数加到另一行，行列式的值不变。

2、求行列式的值   

  

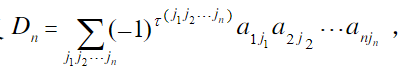
当然这个方法基本没人用。

让根据行列式的一个性质如果行列式呈三角状其他位为0，则行列式的值为对角线上数的乘积

例    a11  a12 a13

　　0      a22 a23

　　0        0    a33

则行列式的值D=a11*a22*a33

我们便可以通过将一个普通行列式变为一个呈三角状的行列式从而求值

这个方法叫做高斯消元法

用第2-n行减去第1行的k倍使an1为零 

然后用第3-n行减去第2行的k倍使an2为零

……

从而达到目的

然后看代码

第一种：

double z[110][110];
int n;
double gauss()
{
    double x=1;
    for (int a=1;a<=n;a++){
        for (int b=a;b<=n;b++)
            if (fabs(z[b][a]) > 1e-8){
                if (b==a) break;
                    x=-x;  //代表这个行列式两行换后的系数变为相反数
                for (int c=1;c<=n;c++)
                   swap(z[b][c],z[a][c]);
                break;
                }//若此行的第a个元素为0则不能用这行去消其他行与不为零的一行换
        if (fabs(z[a][a]) <= 1e-8) return 0.0;//若找不到不为零的一行则此行列式为零
        for (int b=a+1;b<=n;b++){
            double k = z[b][a] / z[a][a];
            for (int c=1;c<=n;c++)
            z[b][c] = z[b][c] - z[a][c] * k;
        }//消元过程
    }
}

此方法足以应对绝大多数题目，但缺点是double k = z[b][a] / z[a][a];精度不足

于是用第a个数最大的那行去消精度误差最小

得到第二种：

double z[110][110];
int n;
double gauss()
{
    double x=1;
    for (int a=1;a<=n;a++){
        for (int b=a+1;b<=n;b++)
            if (fabs(z[b][a]) > fabs(z[a][a])){
                x=-x;
                for (int c=1;c<=n;c++)
                    swap(z[b][c],z[a][c]);
            }
    if (fabs(z[a][a]) <= 1e-8) return 0.0;
    for (int b=a+1;b<=n;b++){
        double k = z[b][a] / z[a][a];
        for (int c=1;c<=n;c++)
            z[b][c] = z[b][c] - z[a][c] * k;
        }
    }
    for (int a=1;a<=n;a++)
        x=x*z[a][a];
    return x;
}

第三种主元消元法：

int n,z[110][110];
int gauss()
{
    int x=1;
    for (int a=1;a<=n;a++){
        for (int b=a+1;b<=n;b++){
            while (z[b][a]!=0){
                int k = z[a][a] / z[b][a];
                for (int c=1;c<=n;c++)
                    z[a][c] = z[a][c] - z[b][c] * k;
                for (int c=1;c<=n;c++)
                    swap(z[a][c],z[b][c]);
                x=-x;
            }
        }
    }
    for (int a=1;a<=n;a++)
        x=x*z[a][a];
    return x;
}