神经网络

     VGGNet与Inception出现后， 学者们将卷积网络不断加深以寻求更优越的性能， 然而随着网络的加深， 网络却越发难以训练， 一方面会产生梯度消失现象； 另一方面越深的网络返回的梯度相关性会越来越差，接近于白噪声， 导致梯度更新也接近于随机扰动。

    ResNet（Residual Network， 残差网络） 较好地解决了这个问题， 并获得了2015年ImageNet分类任务的第一名。 此后的分类、 检测、 分割等任务也大规模使用ResNet作为网络骨架。

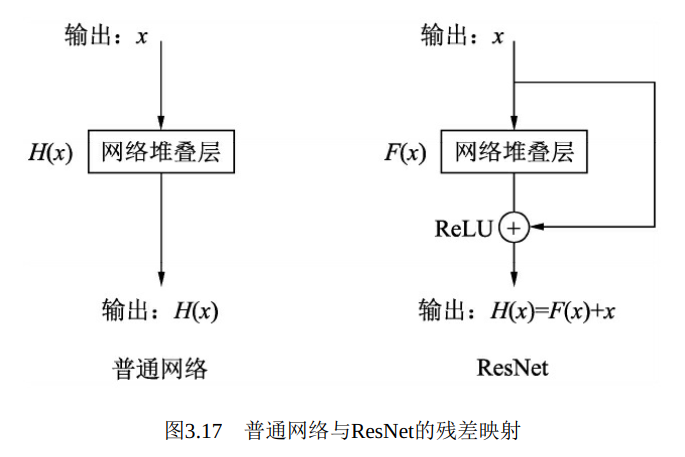
    ResNet的思想在于引入了一个深度残差框架来解决梯度消失问题，即让卷积网络去学习残差映射， 而不是期望每一个堆叠层的网络都完整地拟合潜在的映射（拟合函数） 。 如图3.17所示， 对于神经网络， 如果我们期望的网络最终映射为H(x)， 左侧的网络需要直接拟合输出H(x)，而右侧由ResNet提出的子模块， 通过引入一个shortcut（捷径） 分支， 将需要拟合的映射变为残差F(x)： H(x)-x。 ResNet给出的假设是： 相较于直接优化潜在映射H(x)， 优化残差映射F(x)是更为容易的。

    在ResNet中， 上述的一个残差模块称为Bottleneck。 ResNet有不同网络层数的版本， 如18层、 34层、 50层、 101层和152层， 这里以常用的50层来讲解。 ResNet-50的网络架构如图3.18所示， 最主要的部分在于中间经历了4个大的卷积组， 而这4个卷积组分别包含了3、 4、 6这3个Bottleneck模块。 最后经过一个全局平均池化使得特征图大小变为1×1，然后进行1000维的全连接， 最后经过Softmax输出分类得分。

 

    由于F(x)+x是逐通道进行相加， 因此根据两者是否通道数相同， 存在两种Bottleneck结构。 对于通道数不同的情况， 比如每个卷积组的第一个Bottleneck， 需要利用1×1卷积对x进行Downsample操作， 将通道数变为相同， 再进行加操作。 对于相同的情况下， 两者可以直接进行相加。
    利用PyTorch实现一个带有Downsample操作的Bottleneck结构， 新建一个resnet_bottleneck.py文件， 代码如下：

   

import torch.nn as nn

class Bottleneck(nn.Module):

    def __init__(self, in_dim, out_dim, stride=1):

        super(Bottleneck, self).__init__()
        # 网路堆叠层是由1×1、 3×3、 1×1这3个卷积组成的， 中间包含BN层
        self.bottlenceck = nn.Sequential(
                nn.Conv2d(in_dim, in_dim, 1, bias=False),
                nn.BatchNorm2d(in_dim),
                nn.ReLU(inplace=True),
                nn.Conv2d(in_dim, in_dim, 3, 1, 1, bias=False),
                nn.BatchNorm2d(in_dim),
                nn.ReLU(inplace=True),
                nn.Conv2d(in_dim, out_dim, 1, bias=False),
                nn.BatchNorm2d(out_dim)
        )

        self.relu = nn.ReLU(inplace=True)
        # Downsample部分是由一个包含BN层的1×1卷积组成
        self.downsample = nn.Sequential(
                nn.Conv2d(in_dim, out_dim, 1, 1),
                nn.BatchNorm2d(out_dim)
        )

    def forward(self, x):
        identity = x
        out = self.bottlenceck(x)
        identity = self.downsample(x)

        # 将identity（恒等映射） 与网络堆叠层输出进行相加， 并经过ReLU后输出
        out += identity 
        out = self.relu(out)
        return out

import torch
from resnet_bottleneck import Bottleneck

# 实例化Bottleneck， 输入通道数为64， 输出为256， 对应第一个卷积组的第一个Bottleneck
bottleneck_1_1 = Bottleneck(64, 256).cuda()
print(bottleneck_1_1)
# Bottleneck作为卷积堆叠层， 包含了1×1、 3×3、 1×1这3个卷积层
>>  Bottleneck(
        (bottlenceck): Sequential(
            (0): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
            (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
            (2): ReLU(inplace=True)
            (3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
            (4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
            (5): ReLU(inplace=True)
            (6): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
            (7): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
        (relu): ReLU(inplace=True)
        # 利用Downsample结构将恒等映射的通道数变为与卷积堆叠层相同， 保证可以相加
        (downsample): Sequential(
            (0): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1))
            (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
    )

input = torch.randn(1, 64, 56, 56).cuda()
output = bottleneck_1_1(input) # 将输入送到Bottleneck结构中
print(input.shape)
>> torch.Size([1, 64, 56, 56])

print(output.shape)
# 相比输入， 输出的特征图分辨率没变， 而通道数变为4倍
>> torch.Size([1, 256, 56, 56])