决策树解决的是分类问题
特征选择:选择一个合适的特征作为判断节点,可以快速的分类,减少决策树的深度。决策树的目标就是把数据集按对应的类标签进行分类。最理想的情况是,通过特征的选择能把不同类别的数据集贴上对应类标签。特征选择的目标使得分类后的数据集比较纯。如何衡量一个数据集纯度,这里就需要引入数据纯度函数。下面将介绍两种表示数据纯度的函数
树的最大深度怎么选择?
一组数据有若干特征,建立一个多叉树,使得给出一个数据,都能根据该树从根走到叶节点,即判别分类
1、基于信息增益最大的ID3算法
首先该选取哪一个特征值呢?基于信息增益最大的思想如下:
(1)首先根据将全部的数据根据类别划分为两类(是或者否),然后求总体的熵,s(D) = -(是的概率)lg(是的概率) - (否的概率)lg(否的概率)
(2)在每一个特征的情况下求条件熵,假设每一个数据有A, B, C, D四个特征,A的特征取值位a1, a2, a3, B的特征取值为b1, b2, C的特征取值为c1, c2, D的特征取值为d1,d2,d3,在A特征下的条件熵就是 将取出数据中所有A值为a1, a2, a3,形成三组数据,然后对于A=a1的数据,用(1)的方法求熵,同样对A=a2,A=a3也是...
此时可以得出在A特征下的条件熵位 s(D|A) = (a1集合的概率)(a1集合里的熵) + (a2集合的概率) (a2集合里的熵) + (a3集合的概率)(a3集合里的熵)最后可以求得A的信息增益 g(D, A) = s(D) - s(D|A) 信息增益的意思就是说,在选取A的情况下,将这个集合分类正确的可能性提高的大小
然后依次求 B, C, D的信息增益,选取最大的特征(A,B, C, D) 作为根节点
(3)假设上一步选取的最大特征是A,那么以A作为根节点,下面有a1, a2, a3,三个分支, 对于分支a1的结果就要分析所有A=a1的集合的情况,如果全为是或者否表示此时分类完成, 如果既有是也有否,那么按照(2)的方法,在求 (B, C, D)的信息增益
缺点:
1、没有考虑连续值,如长度,因为熵是基于离散情况的
2、优选选择种类较多的特征
3、没有处理缺失值
2、基于信息增益比的C4.5算法
信息增益比 = 信息增益 / 特征的熵, 算法同信息增益一样
信息增益比比信息增益好在哪里? 参考https://www.cnblogs.com/muzixi/p/6566803.html
以预测天气的数据为例,假设有一个特征为日期,那么根本这个日期划分的话,只需要两层树就结束了,所以为了克服这种特征,划分的太细,引入信息增益比,它在信息增益的前提下有一个权值,即这维特征的一个权值,而这个权值是怎么计算的呢,它是这维特征的特征取值熵,信息增益比越大就会越优先
这里有一个细节:根据信息增益进行选择的时候,倾向于选择特征值多的属性,但是根据信息增益比进行选择的时候容易选择特征值少的属性,解决方法是:不是直接选择增益率最大的候选划分属性,而是采用一个启发式,先从候选划分属性中找出信息增益高于平均水平的属性,在从中选择增益率最高的。
3、基于基尼指数的CART
假设数据种类一共有k类,则样本的基尼指数 = 1 - (第一类概率的平方 + 第二类概率的平方 + ... + 第k类概率的平方)
基尼指数衡量的是集合的不确定性,基尼指数越大,集合的不确定性越大,同熵的性质一样
基于基尼指数的CART,每次选取最小的基尼指数的集合,因为这个比较稳定
为什么会产生基尼指数呢?(需要调研一下)
由下图可以看出基尼指数是熵的一个近似代替,与熵而言,基尼指数计算简答,熵中有复杂的对数计算, 基尼指数也是误差的近似替代
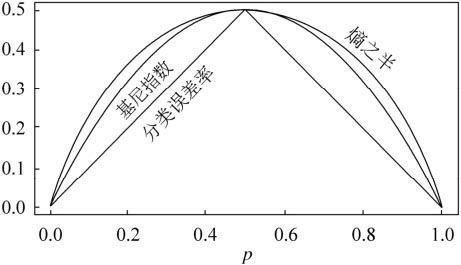
https://www.zhihu.com/question/36659925/answer/223255104
4、剪枝(西瓜书讲的挺好)
前剪枝:在创建的时候确定要不要创建该分支,如果创建了该分支后判断的准确率 < 不创建该分支判断的准确率, 减掉
后剪枝:创剪完整个树后,从下往上进行判断,剪枝
CART剪枝算法(Cost-Complexity Pruning)
过程:
(1)、首先生成一棵完整的决策树T0
(2)自下而上地对每一个非叶节点t,计算g(t) = ( C(t) - C(Tt) ) / ( |L(Tt)| - 1),得到g(ti)集合,并记录下最小的那个g(ti)的节点t0。g(t)就是误差增益率,剪枝前与剪枝后的误差对比,越小越需要剪枝,可以想像,如果对于两个节点剪枝后误差增益相同,即分母相同,一个节点剪枝前是100个节点,一个节点剪枝前是10个节点,所有优先剪掉100个节点的。
(3)对t0为根的子树进行合并成一个叶子节点,此时从【T0】树变成了【T1】树
(4)如果此时【T1】不是根节点单独构成的树,就重复(2)进行剪另一个枝
最后得到一个子树序列{ T0, T1 ... Tk}, 每一个T都代表一种剪枝的策略,这是一个重复的过程,从原始的T,剪一个节点得到T0,然后对于这个T0在进行剪枝得到T1...,Tk就是只有一个节点的树,最后核心就是从中选择最有的一个 T 作为最后的最优子树
如何选择从这个子树序列中选择出最优子树呢?有两种方法:(1)独立剪枝数据集 (2)基于k折交叉验证
交叉验证法:
计算这个子树序列的每一个树在测试集上的误差,取误差最小的树最为剪枝后的最优树
5、连续值与缺省值(西瓜书)
连续值:可以以每一个值作为一个切分点,将原始集合划分成两部分,一部分不大于该数的,另一部分大于该数的, 然后枚举找到最佳的切分点
6、关于决策树的损失函数 https://blog.csdn.net/wjc1182511338/article/details/76793598
为了避免出现过拟合的现象,我们要对决策树进行剪枝。
设决策树的子节点集合为T,t是T中的一个元素,该叶节点有NtNt个样本,其中k类的样本有NtkNtk个,共K个分类
则损失函数可以定义为
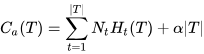
1、ID3
- 没有考虑连续特征,如长度等连续值,限制了ID3的用途
- ID3采用信息增益大的特征优先建立决策树,相同条件下,取值较多的特征比取值少的特征信息增益大,倾向于选择特征取值多的特征。
- ID3对缺失值的情况没有做考虑
- 没有考虑过拟合的问题
2、C4.5
- 连续特征处理: 将连续特征进行离散化,比如m个样本连续特征A有m个,从小到大排序, 相邻的值取平均,会产生m-1个平均值,分别计算以该点作为二元分类时的信息增益,选择信息增益最大的点作为该连续特征的二元离散分类点。与离散属性不同的是,如果该点为连续属性,则该属性后面还能参与子节点的产生选择过程。
- 信息增益偏向与选择取值较多的特征。信息增益比
- 缺失值的处理:为样本设置一个权重
- 如何在属性缺失的情况下进行划分属性选择
- 对于一个有缺失特征值的特征A,我们可以根据是否缺失将它分成两部分,一部分是无缺失值的集合,另一部分是有缺失值的集合,对于无缺失值的集合,我们就可以使用之前的算法进行求信息增益比,最后对这个信息增益比我们乘以一个系数,这个系数就是无缺失值集合中样本权重和与全部数据集合权重和的比值
- 选定了特征划分,在该特征上出现缺失的样本如何处理
- 将缺失特征的样本以不同的概率同时划分到所有的叶子节点,该样本的权重按照各个子节点样本的数量比例进行划分。
- C4.5引入的正则化系数进行剪枝
3、CART
- 二叉树,不是多叉树
- 基于基尼指数,越低越好,比熵的计算快。