力扣343（整数拆分）

343、整数拆分

基本思想：

动态规划

具体实现：

1.确定dp数组以及下标的含义

dp[i]：分拆数组i，可以得到的最大乘积为dp[i]

2.确定递推公式

两种方法得到dp[i]

（1）从1遍历j，j*（i-j），把i拆成了两个数相乘

（2）从1遍历j，j*dp[i-j]，把i拆成立两个以及两个以上相乘

dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j})

3.dp的初始化

dp[2] = 1

4.遍历顺序

dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]

枚举j的时候，是从1开始的。i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

5.举例推导dp数组

代码：

class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1];
        dp[2]=1;
        for (int i = 3; i <= n; ++i){
            for (int j = 1; j < i - 1; ++j){
               dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

96、不同的二叉搜索树

基本思想：

动态规划

具体实现：

1.确定dp数组以及下标的含义

dp[i]：1到i为节点组成的二叉搜索树的个数为dp[i]

2.确定递推公式

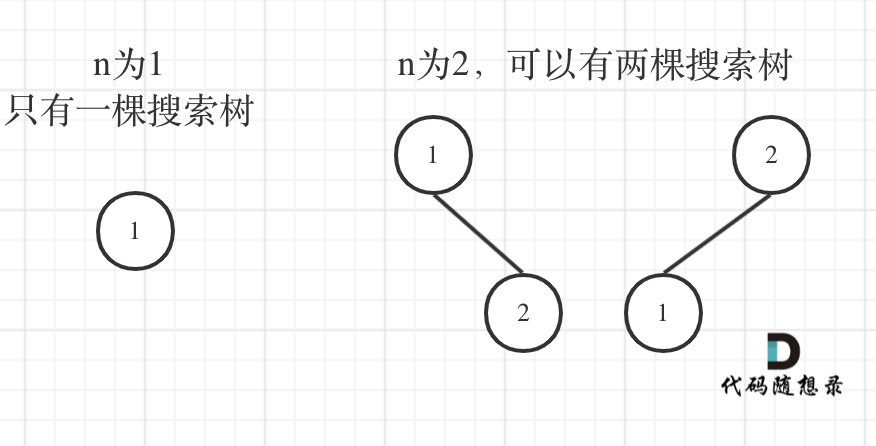
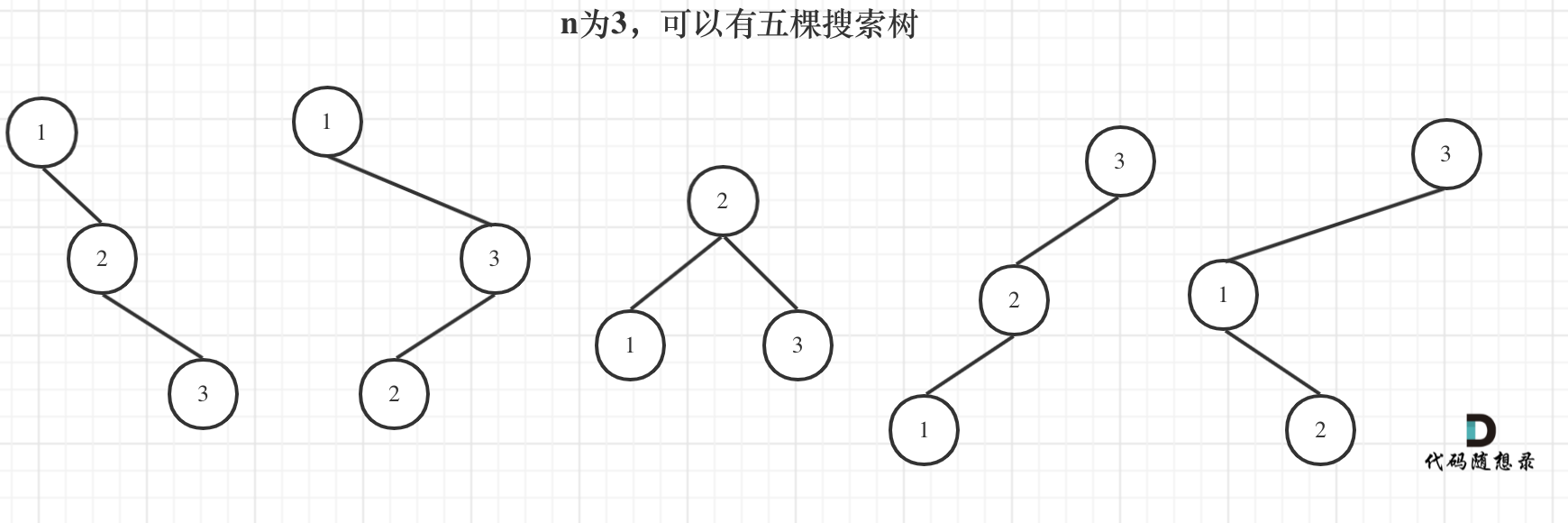
（1）当1为头结点的时候，其右子树有两个节点，这两个节点的布局，和 n 为2的时候两棵树的布局是一样的

 （2）当3为头结点的时候，其左子树有两个节点，这两个节点的布局，和n为2的时候两棵树的布局也是一样的

（3）当2位头结点的时候，其左右子树都只有一个节点，布局和n为1的时候只有一棵树的布局也是一样的

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

（a）元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量=dp[2] * dp[0] 

（b）元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量= dp[1] * dp[1]

（c）元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量=dp[0] * dp[2]

dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

从1遍历j，dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

3.dp数组如何初始化

空节点也是一颗二叉树，dp[0]=1

4.确定遍历顺序

从前向后遍历

5.举例推导

代码：

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++){
            for (int j = 1; j <= i; j++){
                 //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}