力扣37题、22题（回溯算法 解数独 括号生成）

37、解数独

基本思路：

回溯算法、把所有情况试一遍

需要填入数字的格，去掉不可能的数字，每一个可能的数字都要试

具体实现：

1、当填写第i行，第j列的元素时，需要知道其对应的行，列，块中，1-9数字的使用情况，从而选用不同的数字

新建row = [set(range(1, 10)) for _ in range(9)] 记录每一行可用的数字

col = [set(range(1, 10)) for _ in range(9)] 记录每一列可用的数字

block = [set(range(1, 10)) for _ in range(9)] 记录每一块可用的数字

2、if board[i][j] != '.' 碰到的是事先给好的数字，不需要咱们填，

那这个事先给好的数字不能出现在对应的行，列，块可用数字的集合当中

val = int(board[i][j])
row[i].remove(val)
col[j].remove(val)
block[(i // 3)*3 + j // 3].remove(val)

else 碰到的是空格，需要填入数字，把这个位置先记录下来

3、记录好了所用需要填数的空格和每一行每一列每一块可用的数。开始回溯

4、空格的索引，行列索引都好找

块的索引b = (i // 3)*3 + j // 3

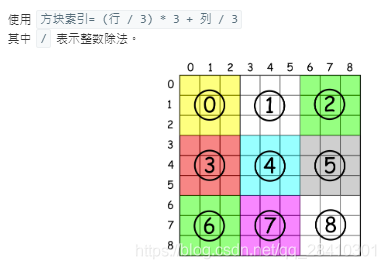
 比如四行五列，就是第四块

5、一个一个试row col block中共同存在的数，这些数都是符合规定的

for val in row[i] & col[j] & block[b]:取交集

6、放入之后代表这个数就不能用了，把这个数在row col block中删掉

row[i].remove(val)
col[j].remove(val)
block[b].remove(val)

7、递归

8、递归完后把这个数再还回来，万一这个数导致后面的数独做不下去了，还能反悔

代码：

def solveSudoku(self, board: List[List[str]]) -> None:
        row = [set(range(1, 10)) for _ in range(9)]  # 行剩余可用数字
        col = [set(range(1, 10)) for _ in range(9)]  # 列剩余可用数字
        block = [set(range(1, 10)) for _ in range(9)]  # 块剩余可用数字

        empty = []  # 收集需填数位置
        for i in range(9):
            for j in range(9):
                if board[i][j] != '.':  # 更新可用数字
                    val = int(board[i][j])
                    row[i].remove(val)
                    col[j].remove(val)
                    block[(i // 3)*3 + j // 3].remove(val)
                else:
                    empty.append((i, j))

        def backtrack(iter=0):
            if iter == len(empty):  # 处理完empty代表找到了答案
                return True
            i, j = empty[iter]
            b = (i // 3)*3 + j // 3
            for val in row[i] & col[j] & block[b]:
                row[i].remove(val)
                col[j].remove(val)
                block[b].remove(val)
                board[i][j] = str(val)
                if backtrack(iter+1):
                    return True
                row[i].add(val)  # 回溯
                col[j].add(val)
                block[b].add(val)
            return False
        backtrack()

基本思想：

套用模板

具体实现：

1、递归函数以及参数

递归函数返回值是bool类型

解数独找到一个符合的条件就立刻返回，

相当于找到从根节点到叶子节点一条唯一路径

2.递归终止条件

不需要，因为遍历整个树形结构寻找可能的叶子节点就立刻返回

3.两个for循环嵌套着递归

一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，确定好位置以后

递归遍历这个位置放9个数字的可能性

如果尝试9个数都不行，说明这个棋盘找不到解决数独问题的姐，直接返回

4.判断棋盘是否合法

代码：

class Solution {
    public void solveSudoku(char[][] board) {
        solveSudokuHelper(board);
    }
    private boolean solveSudokuHelper(char[][] board){
        for (int i = 0; i < 9; i++){
            for (int j = 0;j < 9; j++){
                if (board[i][j] != '.'){ //跳过原始数字
                    continue;
                }
                for (char k = '1';k <= '9'; k++){ //（i，j）这个位置放k是否合适
                    if(isValidSudoku(i,j,k,board)){
                        board[i][j] = k;
                        if(solveSudokuHelper(board)){ //如果找到合适的一组立刻返回，不用求多种解法，找到一种解法就行
                            return true;
                        }
                        board[i][j] = '.'; //递归完后把这个数再还回来，万一这个数导致后面的数独做不下去了，还能反悔
                    }
                }
                return false;//9个数都试完了，都不行就返回false

            }
        }//遍历完没有返回false，说明找到了合适棋盘位置
        return true;
    }
    private boolean isValidSudoku(int row,int col,char val,char[][] board){
        for (int i=0;i<9;i++){ //同行是否重复
            if(board[row][i] == val){
                return false;
            }
        }
        for (int j=0; j < 9; j++){ //同列是否重复
            if(board[j][col] == val){
                return false;
            }
        }
        //九宫格是否重复
        int startRow = (row/3)*3;
        int startCol = (col/3)*3;
        for (int i = startRow; i < startRow +3;i++){
            for(int j= startCol; j < startCol+3; j++){
                if(board[i][j] == val){
                    return false;
                }
            }
        } 
        return true;
    }
}

22、括号生成

基本思想：

回溯算法

具体实现：

1、一个合法的括号组合，左括号数量一定等于右括号数量

2、在放入括号过程中，左括号的数量大于等于右括号的数量

3、left记录已经使用多少个左括号

right记录已经使用多少个右括号

套模板：

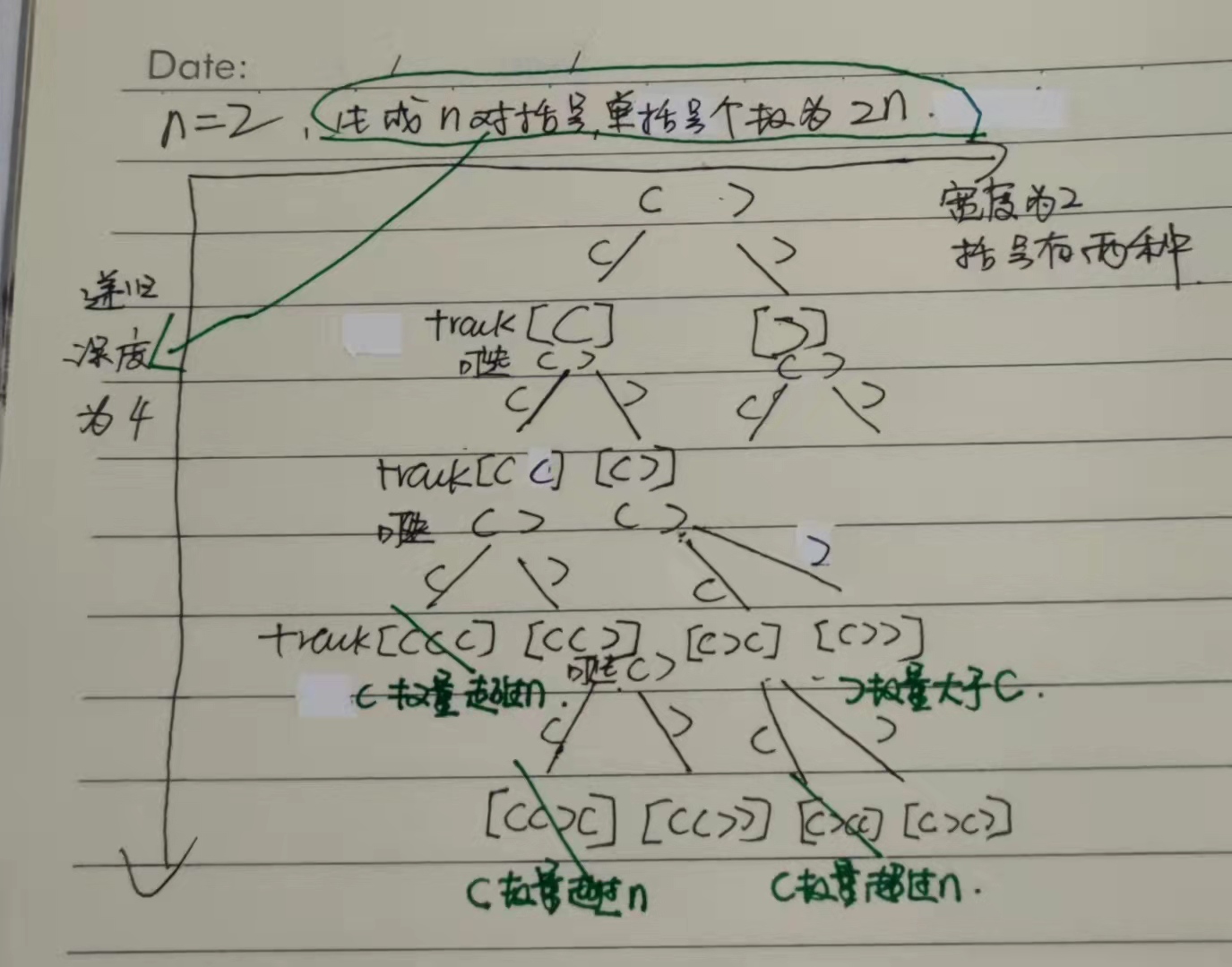
代码：

java

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<String>();
        backtrack(ans, new StringBuilder(), 0, 0, n);
        return ans;
    }

    public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {
        if (cur.length() == max * 2) {
            ans.add(cur.toString());
            return;
        }
        if (open < max) {
            cur.append('(');
            backtrack(ans, cur, open + 1, close, max);
            cur.deleteCharAt(cur.length() - 1);
        }
        if (close < open) {
            cur.append(')');
            backtrack(ans, cur, open, close + 1, max);
            cur.deleteCharAt(cur.length() - 1);
        }
    }
}

 python

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        ans = []
        def backtrack(S, left, right):
            if len(S) == 2 * n:
                ans.append(''.join(S))
                return
            if left < n:
                S.append('(')
                backtrack(S, left+1, right)
                S.pop()
            if right < left:
                S.append(')')
                backtrack(S, left, right+1)
                S.pop()

        backtrack([], 0, 0)
        return ans