416、分割等和子集
基本思想:
动态规划-01背包--一个商品只能放一次
- 背包的体积为sum/2
- 背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为sum/2的子集
- 背包中每一个元素是不可重复放入
具体实现:
1、确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值可以最大为dp[j]。
套入本题,dp[j]表示:容量为j的背包,最大可以凑成j的子集总和为dp[j]。
2、状态转移方程
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题中,相当于背包里放入数值,物品i的重量是nums[i],价值也是nums[i]
递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3、初始状态
dp数组都初始化为0
4、确认遍历顺序
使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒叙遍历
5、举例推导dp数组
dp[i]的数值一定是小于等于i的
如果dp[i] == i 说明,集合中的子集总和正好可以凑成总和i

dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
代码:
class Solution { public boolean canPartition(int[] nums) { if(nums == null || nums.length == 0) return false; int n= nums.length; int sum = 0; for(int num : nums){ sum += num; } if(sum % 2 != 0) return false; int target = sum/2; int[] dp = new int[target + 1]; for(int i = 0; i < n; i++){ for (int j = target; j >= nums[i]; j--){ dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]); } } return dp[target] == target; } }
1049、最后一块石头的重量
基本思想:
尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,化解为01背包
本题物品的重量为store[i],物品的价值也为store[i]。
对应着01背包里的物品重量weight[i]和 物品价值value[i]。
具体实现:
1.确定dp数组以及下标的含义
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背dp[j]这么重的石头。
2.确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3.dp数组初始化
dp数组初始化为0
4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒叙遍历
5.举例推导dp数组
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
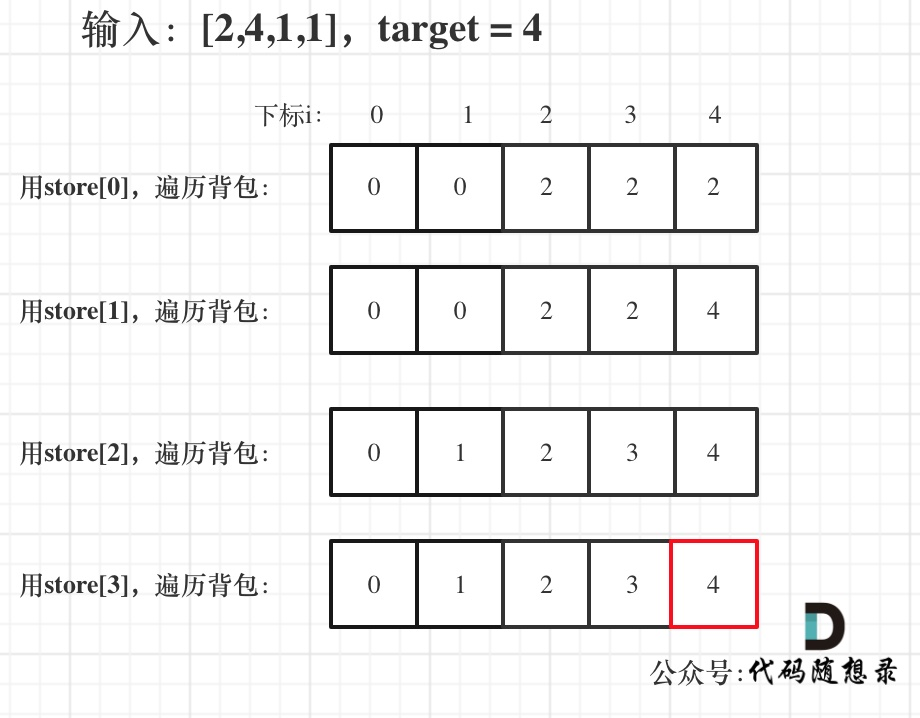
最后dp[target]里是容量为target的背包所能背的最大重量。
分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
在计算target的时候,target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]的。
那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。
代码:
class Solution { public int lastStoneWeightII(int[] stones) { int sum = 0; for (int i : stones){ sum += i; } int target = sum >> 1; int[] dp = new int[target + 1]; for (int i = 0; i < stones.length; i++){ for (int j = target; j >= stones[i]; j--){ dp[j] = Math.max(dp[j],dp[j-stones[i]] + stones[i]); } } return sum - 2 * dp[target]; } }
494、目标和
基本思想:
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
因为每个物品(题目中的1)只用一次,所以是01背包
具体实现:
1.确定dp数组以及下标的含义
dp[ i ][ j ]表示:从数组nums中 0 - i 的元素进行加减可以得到 j 的方法数量。
从下标为[0-i]的数中任意取,填满j(包括j)这么大容积的包,有dp[ i ][ j ]种方法
2.确定递推公式
dp[ i ][ j ] 的来源
两个方向推导
- j<nums[i] 因为容量不够,不放nums[i]:dp[i][j]=dp[i-1][j]
- j>=nums[i] 容量够:
dp[i][j] =dp[i-1][j](不放nums[i]时的方法数)+dp[i-1][j - nums[i]](背包容量空出一个nums[i]的位置,剩余容量的方法数,因为再加上nums[i]不需要另算一种方法)- 意思就是我有两条路到终点,到终点之前有一条必经之路,这条必经之路不影响我还是两条路到终点
3.初始化
(1)背包容量为0时的唯一方法就是什么也不放
(2)如果第一个物品他的重量为0,那么背包容量为0时就有两种情况,一种是放入这个重量为0的物品,一种是啥也不放
如果第一个物品的重量不是0,那么当背包容量正好等于这个物品重量时,就一定有一种方法
4.遍历顺序
从前到后,从上到下
5.举例

class Solution { public int findTargetSumWays(int[] nums, int target) { int sum = 0; for (int i = 0; i < nums.length; i++) sum += nums[i]; if ((target + sum) % 2 != 0) return 0; int size = (target + sum) / 2; if(size < 0) size = -size; int[][] dp = new int[nums.length][size + 1]; for (int i = 0; i < nums.length; i++){ dp[i][0] = 1; } if(nums[0] == 0){ dp[0][0] = 2; } else { for (int j = 0; j <= size; j++){ if (j == nums[0]){ dp[0][j] = 1; } } } for (int i = 1; i < nums.length; i++) { for (int j = 0; j <= size; j++) { if (j < nums[i]){ dp[i][j] = dp[i-1][j]; }else { dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]; } } } return dp[nums.length-1][size]; } }
优化:
class Solution { public int findTargetSumWays(int[] nums, int target) { int sum = 0; for (int i = 0; i < nums.length; i++) sum += nums[i]; if ((target + sum) % 2 != 0) return 0; int size = (target + sum) / 2; if(size < 0) size = -size; int[] dp = new int[size + 1]; dp[0] = 1; for (int i = 0; i < nums.length; i++) { for (int j = size; j >= nums[i]; j--) { dp[j] += dp[j - nums[i]]; } } return dp[size]; } }
474、0和1
基本思想:
动态规划
本题中strs 数组里的元素就是物品,每个物品都是一个
而m 和 n相当于是一个背包,两个维度的背包。
本题其实是01背包问题
这不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
具体实现:
1、确定状态:
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
2、状态转移方程:
多琢磨01背包基础
没优化的
dp[i][j][k]=max(dp[i−1][j−当前字符串使用0的个数][k−当前字符串使用1的个数]+1,当前容量下没放当前字符串的个数)
优化的
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
3、初始化:
01背包的dp数组初始化为0就可以。
4、遍历顺序
优化的需要从后往前
5、举例
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
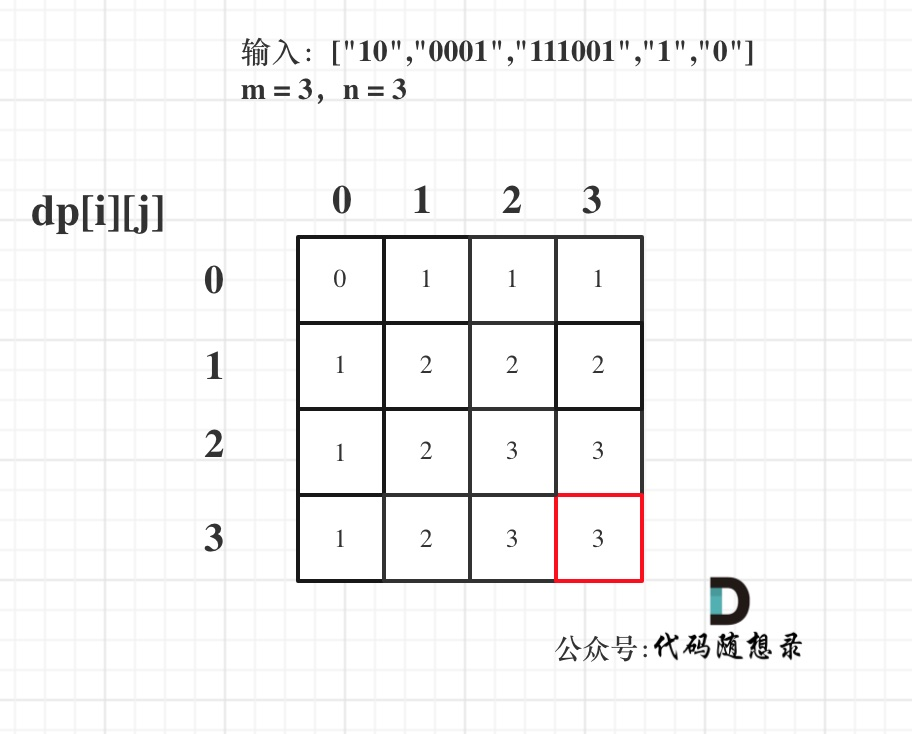
代码:
class Solution { public int findMaxForm(String[] strs, int m, int n) { //dp[i][j]表示i个0和j个1时的最大子集 int[][] dp = new int[m + 1][n + 1]; int oneNum, zeroNum; for (String str : strs) { oneNum = 0; zeroNum = 0; for (char ch : str.toCharArray()) { if (ch == '0') { zeroNum++; } else { oneNum++; } } //倒序遍历 for (int i = m; i >= zeroNum; i--) { for (int j = n; j >= oneNum; j--) { dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1); } } } return dp[m][n]; } }