力扣704题、34题（二分查找）

704、二分查找

基本思想：

• 如果目标值等于中间元素，则找到目标值。
• 如果目标值较小，继续在左侧搜索。
• 如果目标值较大，则继续在右侧搜索。

具体实现：

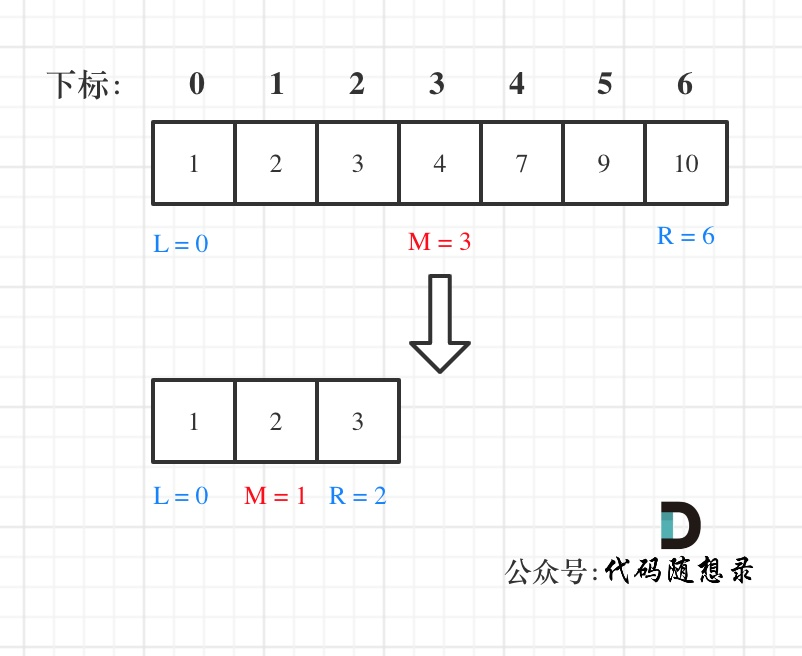
1、搜索时是在闭区间[left,right]，target定义在这个区间内

初始化right的赋值是len(nums)-1，是最后一个元素的索引，

• while循环中的条件是<=  不是=
• if （nums[middle] >targrt）   right = middle-1
• if （nums[middle] < target） left = middle +1

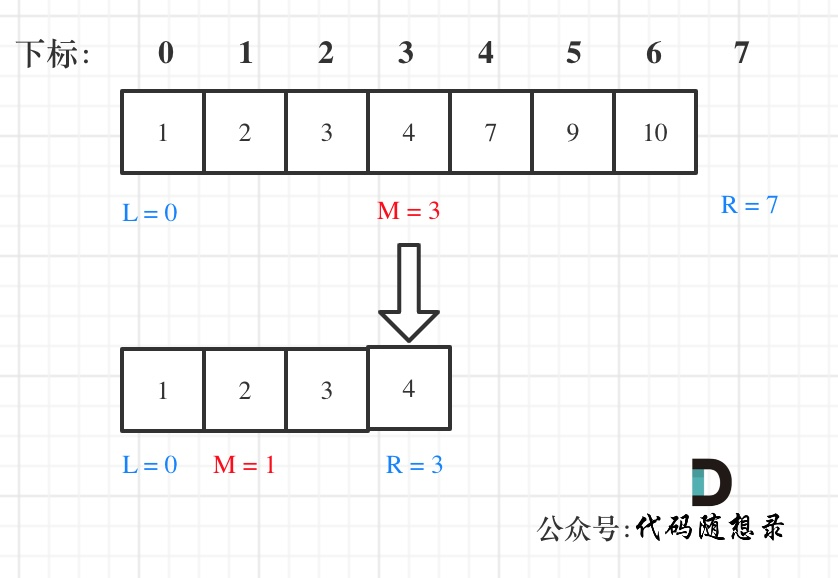
2、搜索时在半开半闭区间[left,right)，target定义在这个区间

初始化right的赋值是len(nums)

• while循环中的条件是<  不是<=，因为left == right在区间[left,right)无意义
• if （nums[middle] >targrt）   right = middle，去左区间寻找，而寻找区间是左闭右开的，所以right更新为middle

• if （nums[middle] < target） left = middle +1

代码：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = int(left + (right-left)/2)
            # mid = left + (right-left)//2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            elif nums[mid] > target:
                right = mid -1
        return -1

第一种情况

class Solution {
    public int search(int[] nums, int target) {
        if (target < nums[0] || target > nums[nums.length -1]){
            return -1;
        }
        int left = 0, right = nums.length - 1;
        while (left <= right){
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target){
               return mid; 
            }
            else if (nums[mid] < target) {
                left = mid +1;
            }
            else {
                right = mid - 1;
            }
        }
        return -1;
    }
}

第二种情况

class Solution {
    public int search(int[] nums, int target) {
        if (target < nums[0] || target > nums[nums.length -1]){
            return -1;
        }
        int left = 0, right = nums.length;
        while (left < right){
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target){
               return mid; 
            }
            else if (nums[mid] < target) {
                left = mid +1;
            }
            else {
                right = mid ;
            }
        }
        return -1;
    }
}

34、在排序数组中查找元素的第一个和最后一个元素

基本思想：

寻找左侧边界的二分搜索

具体实现：

1.二分搜索中没有return -1，如果nums中不存在target这个值，还是会返回left

eg nums=[2,3,5,7]

target = 1,返回0，含义是nums中小于1的个数有0个

target = 8，返回4，含义是nums中小于8的个数有4个

这些返回的数会送去验证，验证是否是目标数

2、nums=[5,7,7,8,8,10] target=8

先得出靠左侧的8的下标=3，赋值给a

再让target+1=9，

没有找到9，但是会返回nums中比9小的数的个数有5个

返回5，赋值给b

3、第一个大于target的位置-1

得出答案[3,4]

4、假如找不到target，进行验证后返回[-1,-1]

代码：

class Solution(object):
    def searchRange(self,nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        def left_func(nums,target):
            n = len(nums)
            left = 0
            right = n -1
            while(left <= right):
                mid = left + (right-left) // 2
                if nums[mid] >= target:
                    right = mid - 1
                if nums[mid] < target:
                    left = mid + 1
            return left
        a =  left_func(nums,target)
        b = left_func(nums,target+1)
        if  a == len(nums) or nums[a] != target:
            return [-1,-1]
        else:
            return [a,b-1]

java

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int a = binarySearch(nums, target);
        int b = binarySearch(nums, target + 1);
        if (a == nums.length || nums[a] != target){
            return new int[]{-1,-1};
        }
        else{
            return new int[]{a,b-1};
        }
    }
    public int binarySearch(int[] nums, int target){
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left <= right){
            int mid = left + ((right - left) >> 1);
            if (nums[mid] >= target){
                right = mid - 1; 
            }
            else  {
                left = mid +1;
            }
        }
        return left;
        
    
    }
}