力扣509题、70题（斐波那契数列、爬楼梯）

509、斐波那契数列

基本思想：

动态规划，滚动数组思想

具体实现：

循环n-1次

 动态递归五部：

1.确定dp数组以及下标的含义

dp[i]的定义为：第i个数的斐波那契数值是dp[i]

2.确定递推公式

状态转移方程dp[i] = dp[i - 1] + dp[i - 2]

3.dp数组如何初始化

dp[0] = 0;

dp[1] = 1;

4.确定遍历顺序

从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，

那么遍历的顺序一定是从前到后遍历的

5.举例推导dp数组

n为10的dp数组

0 1 1 2 3 5 8 13 21 34 55

 代码：

class Solution:
    def fib(self, n: int) -> int:
        if n<2:
            return n
        dp = [0]*(n+1)
        dp[1] = dp[2] = 1
        for i in range(3,n+1):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[n]

class Solution {
    public int fib(int n) {
        if (n <= 1) return n;
        int[] dp = new int[n+1];
        dp[0] = 0;
        dp[1] = 1;
        for (int index = 2; index <= n; index++){
            dp[index] = dp[index - 1] + dp[index -2];
        }
        return dp[n];
    }
}

class Solution:
    def fib(self, n: int) -> int:
        if n < 2:
            return n
        
        p, q, r = 0, 0, 1
        for i in range(2, n + 1):
            p, q = q, r
            r = p + q
        
        return r

class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int p = 0, q = 1, r = 0;
        for (int i = 1; i < n; i++) {
            r = p + q;
            p = q;
            q = r;
        }
        return r;
    }
}

70、爬楼梯

基本思想：

动态规划

具体实现：

1、确定dp数组及其含义

dp[i]:爬到第i层楼梯，有dp[i]种方法

2、确定递推公式

dp[i-1]，上i-1层楼梯，有dp[i-1]种方法，再一步跳一个台阶就是dp[i]

dp[i-2]，上i-2层楼梯，有dp[i-2]种方法，再一步跳两个台阶就是dp[i]

dp[i] = dp[i-1]+dp[i-2]

3、dp数组如何初始化

dp[1] = 1，dp[2] = 2，从i=3开始递推

4、确定遍历顺序

从递推公式看出，遍历顺序是从前往后

5、举例推导dp数组

n=5的时候

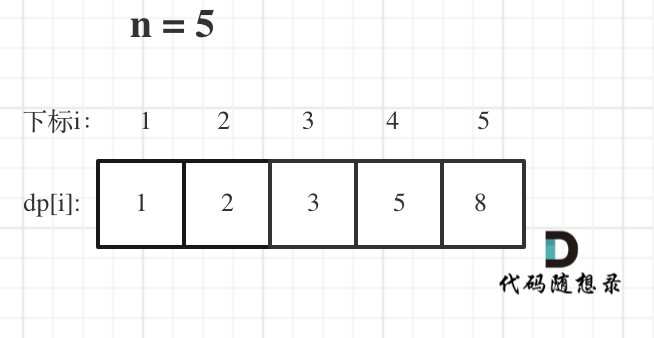
代码：

class Solution {
   public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        if (n <= 1) return n;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

优化：

class Solution {
   public int climbStairs(int n) {
        if (n <= 1) return n;
        int[] dp = new int[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
}