畅通工程(2020.12.17更新)
省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可)。经过调查评估,得到的统计表中列出了有可能建设公路的若干条道路的成本。现请你编写程序,计算出全省畅通需要的最低成本。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出评估的道路条数 N、村庄数目M ( < 100 );随后的 N
行对应村庄间道路的成本,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间道路的成本(也是正整数)。为简单起见,村庄从1到M编号。当N为0时,全部输入结束,相应的结果不要输出。
行对应村庄间道路的成本,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间道路的成本(也是正整数)。为简单起见,村庄从1到M编号。当N为0时,全部输入结束,相应的结果不要输出。
Output
对每个测试用例,在1行里输出全省畅通需要的最低成本。若统计数据不足以保证畅通,则输出“?”。
SampleInput
3 3
1 2 1
1 3 2
2 3 4
1 3
2 3 2
0 100
SampleOutput
3
?
kruskal(克鲁斯卡尔)算法
解析:目前只学了kruskal算法,所以只会用这种,其实所有的畅通工程都是一样的。像学长说的那样就是贪心+并查集,
没了就是这两种。先将每条路拿出来,然后根据每条路的权值进行排序,然后从大到小依次向外拿,并且需要进行查看
是否已被标记,若没有则可以将这条路算入节点中,直到把每条路遍历,最后得出的答案就是对的。(今天听了学长
讲课才懂了这个)
1 #include <stdio.h> 2 #include <string.h> 3 #include <algorithm> 4 using namespace std; 5 int n,m,pre[105]; 6 struct node//存放数据 7 { 8 int x,y,data; 9 }s1[105]; 10 void init()//先初始化,并查集的内容 11 { 12 for(int i=1;i<=n;i++) 13 { 14 pre[i]=i; 15 } 16 } 17 int fun(int x)//查找根节点,记住最好要压缩路径 18 { 19 int r=x; 20 while(r!=pre[r]) 21 { 22 r=pre[r]; 23 } 24 int i=x,j; 25 while(i!=j) 26 { 27 j=pre[i]; 28 pre[i]=r; 29 i=j; 30 } 31 return r; 32 } 33 bool cmp(const node &t1,const node &t2)//重载 34 { 35 return t1.data<t2.data; 36 } 37 int main(void) 38 { 39 while(scanf("%d%d",&n,&m)&&n) 40 { 41 init(); 42 for(int i=1;i<=n;i++) 43 { 44 scanf("%d%d%d",&s1[i].x,&s1[i].y,&s1[i].data); 45 } 46 sort(s1+1,s1+n+1,cmp);//对数据惊进行排序 47 int cont=m,sum=0,x,y; 48 for(int i=1;i<=n;i++) 49 { 50 x=fun(s1[i].x); 51 y=fun(s1[i].y); 52 if(x!=y) 53 { 54 sum+=s1[i].data; 55 cont--; 56 pre[y]=x; 57 } 58 } 59 if(cont==1) 60 printf("%d\n",sum); 61 else 62 printf("?\n"); 63 } 64 }
Prim(普利姆)算法
解析:先随意选择一个顶点加到顶点集 U 里,然后其他顶点属于顶点集 V-U 里,在这两个顶点集之间选择一条最小的边,然后将 V-U 里连接的那个点加到 U 里,将这个点从 V-U里去除,这样就形成新的两个顶点集,并且更新完两个顶点集后还要更新两个顶点集之间的边(有可能刚开始V-U里某个点跟U没链接,更新完顶点集后就有边可以连接了),然后就这样以此类推选出n-1条边,这些边相加就可以形成最小生成树(如果取最大点也可以这样,只是需要加一个标记数组)。代码里的lowcost数组是存V-U每个点顶点集到U的边长度,closest数组是V-U里的顶点与顶点集U所连接边的那另一个顶点。
具体过程还是以图片看比较好好理解,理论的太繁琐了(数据结构书里的图搞过来的)。
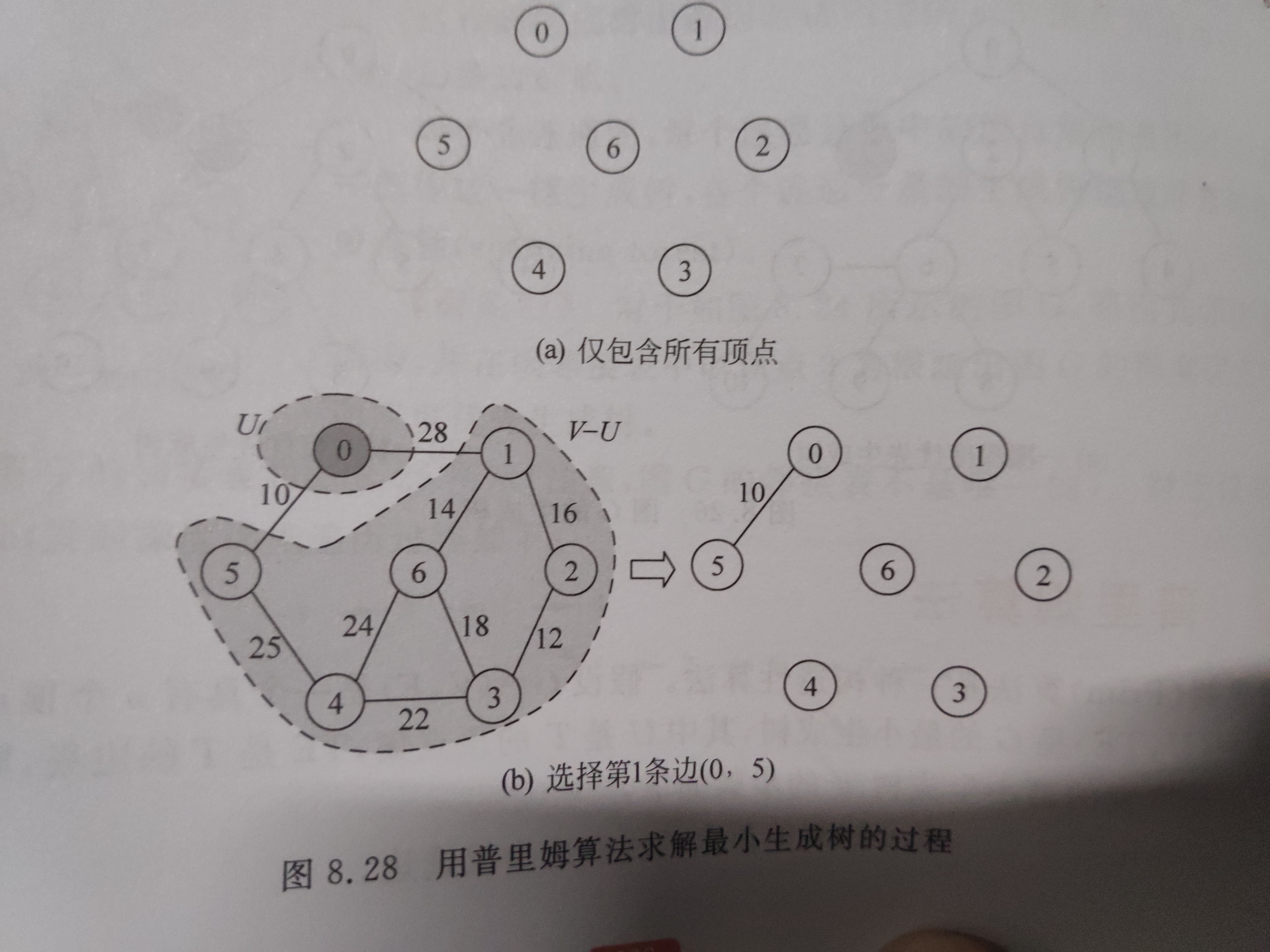
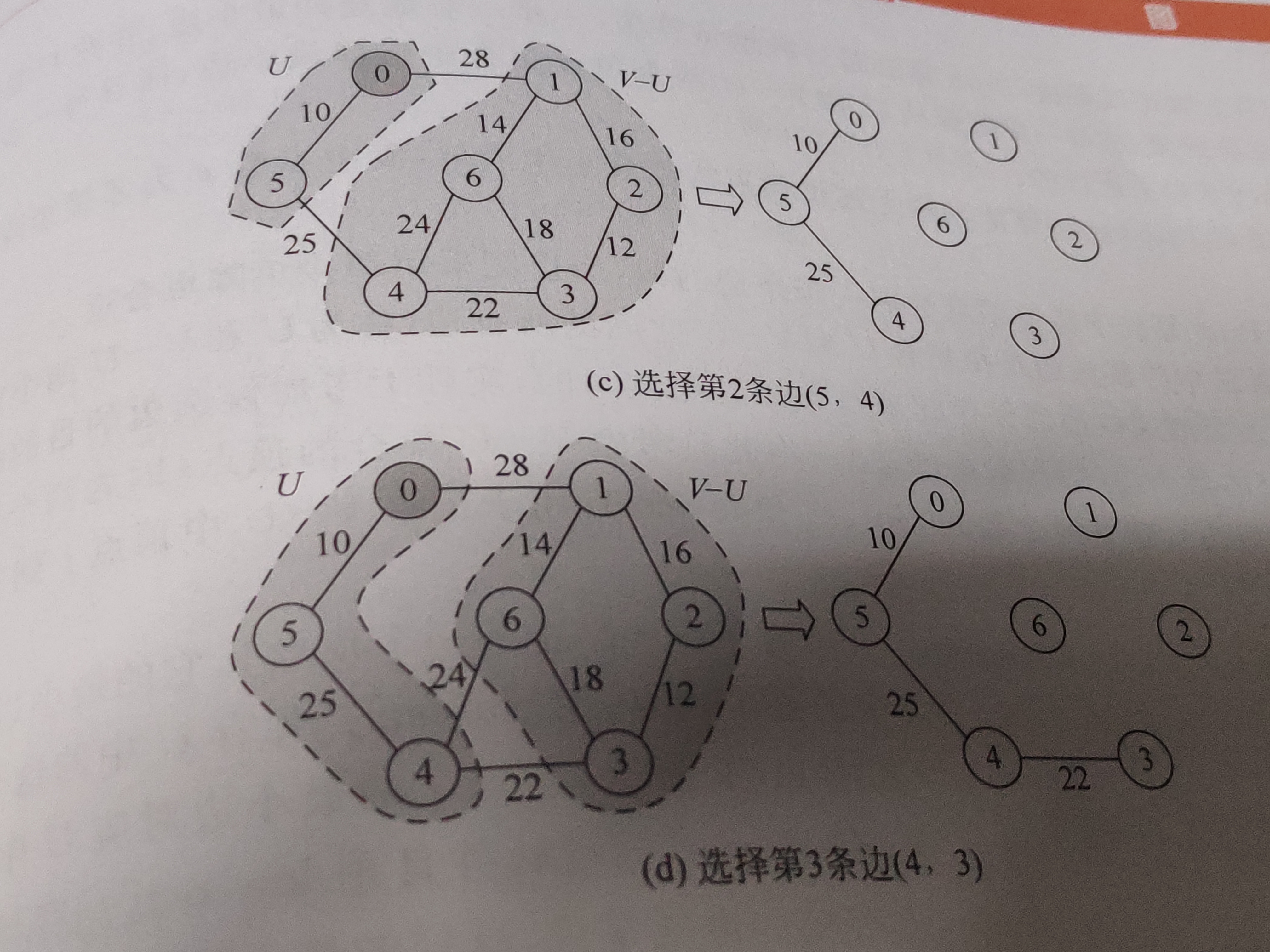

附上代码:
1 #include <cstdio> 2 #include <queue> 3 #include <iostream> 4 #include <algorithm> 5 #include <cmath> 6 #include <bitset> 7 #include <map> 8 #include <stack> 9 #include <stdlib.h> 10 #include <set> 11 #include <cstring> 12 #include <string> 13 #include <vector> 14 #define ll long long 15 #define pi acos(-1) 16 #define mod 1000000007 17 #define INF 0x3f3f3f3f 18 #define exp 1e-8 19 using namespace std; 20 int a[105][105]; 21 int Prim(int n) 22 { 23 int s=1,k,sum=0; 24 int lowcost[105],minx,closest[105]; 25 for(int i=1;i<=n;i++) 26 { 27 lowcost[i]=a[s][i];//V-U里每个点与U的距离 28 closest[i]=s;//V-U里每个点连接的是U里的哪个店,这个这里可以不用 29 } 30 lowcost[s]=0;//这个很重要,s已经在U里了,到自己的距离为0 31 32 for(int i=2;i<=n;i++)//找n-1条边 33 { 34 minx=INF; 35 k=-1; 36 for(int j=1;j<=n;j++)//找最小边 37 { 38 if(lowcost[j]&&lowcost[j]<minx) 39 { 40 minx=lowcost[j]; 41 k=j; 42 } 43 } 44 if(minx==INF)//没有边连接直接退出 45 return -1; 46 lowcost[k]=0;//这个点加到U里 47 sum+=minx;//加上值 48 for(int j=1;j<=n;j++)//更新V-U里每个点到U的边的长 49 { 50 if(lowcost[j]&&a[k][j]<lowcost[j]) 51 { 52 lowcost[j]=a[k][j]; 53 closest[j]=k; 54 } 55 } 56 } 57 return sum; 58 } 59 int main(void) 60 { 61 int n,x,y,w,m; 62 while(scanf("%d%d",&m,&n)) 63 { 64 if(!m) 65 break; 66 memset(a,INF,sizeof(a));//初始化每条边 67 for(int i=1;i<=m;i++) 68 { 69 scanf("%d%d%d",&x,&y,&w); 70 a[x][y]=w;//有时候也要在这里加上判断是不是最短边 71 a[y][x]=w; 72 } 73 int k=Prim(n); 74 if(k!=-1) 75 printf("%d\n",k); 76 else 77 printf("?\n"); 78 } 79 }