Informatica是最常用的ETL工具之一,与之类似的工具还有DataStage和kettle;
由于个人只用过Informatica,所以只讨论Informatica。此软件分为客户端和服务器端连部分,由于我的服务器端连带系统拷贝过来的,所以安装从略。我从使用的角度出发介绍如下:
一、 由于informatica的元数据(账号、密码…)信息保存在Oracle上面,所以我们先来检查下Oracle的运行情况:
- su – oracle先用oracle用户登录到主机,密码是ripple
lsnrctl start监测Oracle的运行
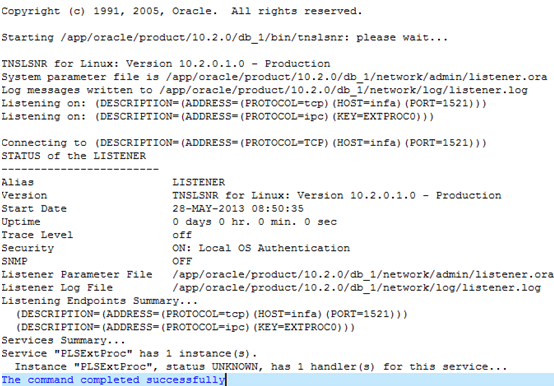
图1.1
OK,现在Oracle正常运行着。
- 登录oracle数据库,sqlplus "/as sysdba"

Exit退出oracle数据库:
退出oracle主机用户:

切换到bin目录
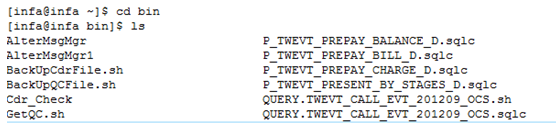
查找启动informatica脚本:

启动该脚本:

由此可以看到我们的服务器启动了
二、 打开Informatica客户端
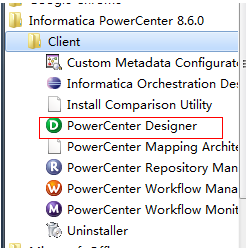
1.0
配置连接
备注:一定要修改windows主机的hosts,地址C:WindowsSystem32driversetc
添加 : 192.168.68.128 infa到文件中,infa就是到时候连接配置的域名,而192.168.68.128就是informatica服务器主机的ip地址。
如图1.1
图1.1
然后我们在cmd里面ping下域名,看看能否解析(ping infa):
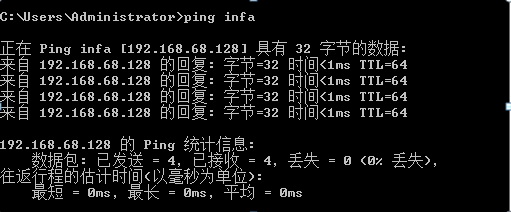
图1.2
从ping出来的结果可以看到infa作域名解析的解析到的ip地址是192.168.68.128,是,(什么!?你不知道为什么ip地址是192.168.68.128),就是我们主机的地址啊
在主机上面执行/sbin/ifconfig
结果如下图:
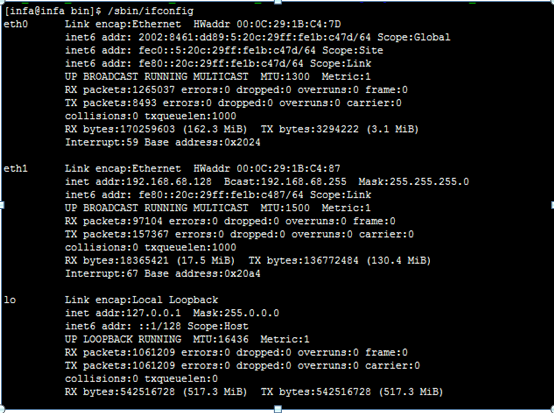
图1.3
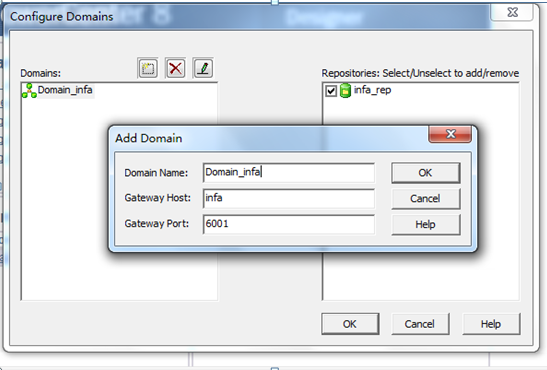
现在可以配置连接了
1.3
其中:
1.Gateway Host就是我们刚才修改那个C:WindowsSystem32driversetc里面的

图1.2
2.Gateway port必须为6001;
3.Domain Name可以随便取;
三、模块介绍:
Informatica总的来说由4大模块组成:
Repository Manager--资料库,Designer--设计器,Workflow Manager--物理设计,Workflow Monitor--监控;
- Repository Manager--资料库,就是保护我们所有设计、实施整个过程的一个类似于宏定义的东西,可以理解为类似informatica的知识存储。
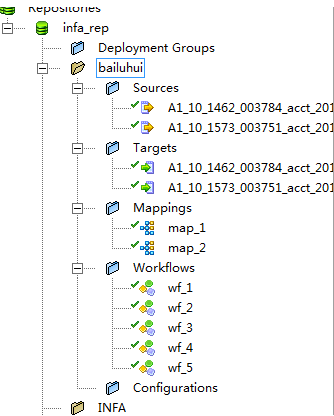
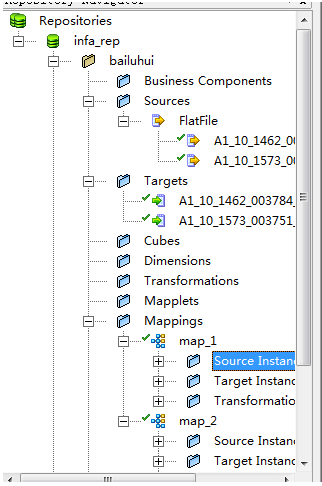
- Designer 设计器,就是单数据流的逻辑过程,打个比方就是某人要怎么样从广州到开平,(方式一是:从广州南站,坐轻轨到新会,再坐野鸡车,到开平市区,再坐个摩托车回家;方式二是:先坐地铁到芳村客运站,然后乘坐大巴回家;。。。)
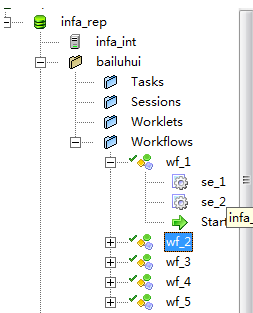
- Workflow Manager--物理设计,即具体的落地实施,比如说是我从广州公司所在地回到我家里。里面保护很多任务设计:task(session/....) workflow(task...)
- Workflow Monitor--监控
Informatica的控制台:
(https://192.168.68.128:8443/adminconsole/Console.do)

用户名:Administrator;密码:Administrator