一 递归调用
递归调用:函数嵌套调用的一种特殊形式。函数在调用时,直接或间接调用的自身
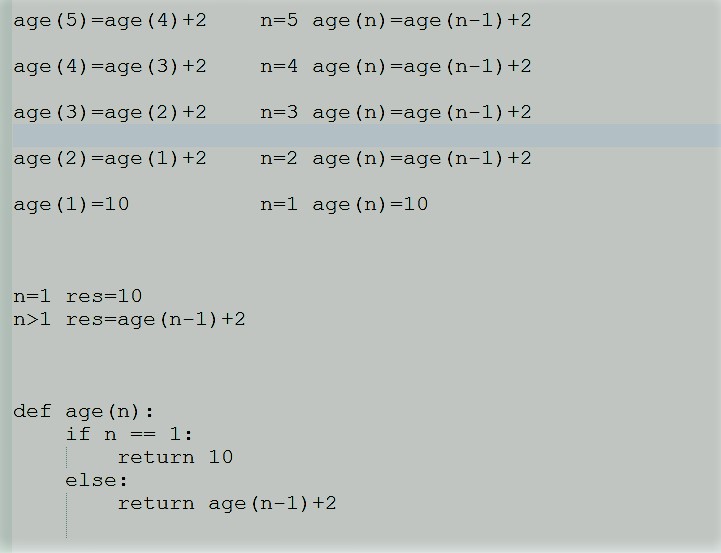
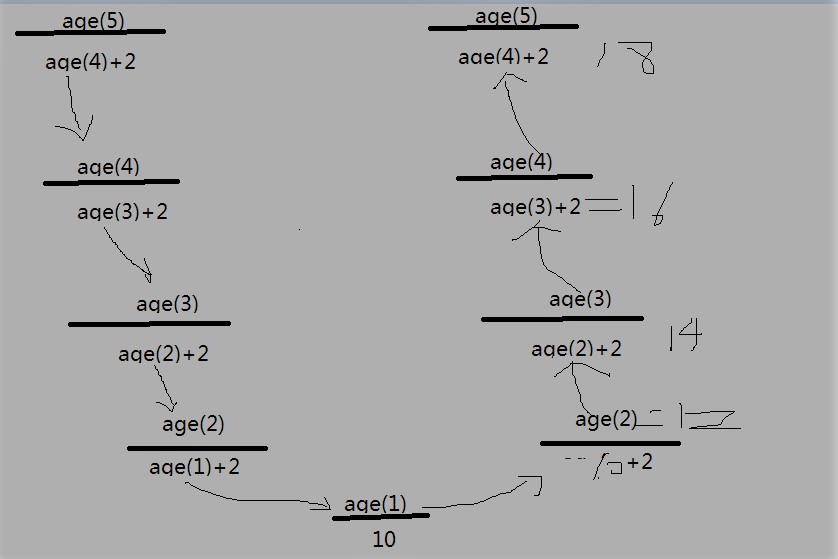
def age(n): if n == 1: return 10 else: return age(n-1)+2 print(age(5)) #18
二 递归特性
1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3. 递归效率不高(①),递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,
每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,
递归调用的次数过多,会导致栈溢出)
**** ① 从理论角度,递归能做的,死循环也能. 比较之下,递归效率 低于 死循环****
三 可修改递归深度

import sys sys.getrecursionlimit() sys.setrecursionlimit(2000) n=1 def test(): global n print(n) n+=1 test() test() 虽然可以设置,但是因为不是尾递归,仍然要保存栈,内存大小一定,不可能无限递归
递归求年龄:
图一
图二
递归年龄代码:
import time
def age(n):
print('----->',n) #便于理解
time.sleep(1) #便于理解
if n == 1: #明确的结束条件
return 10
else:
return age(n-1)+2
print(age(5))
##输出结果
-----> 5
-----> 4
-----> 3
-----> 2
-----> 1
18 #答案
何时用递归?
查询时,问题规模不知循环多少次的时候
二分法

data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35] def search(num,data): print(data) if len(data) > 1: #二分 mid_index=int(len(data)/2) mid_value=data[mid_index] if num > mid_value: #19>18 #num在列表的右边 data=data[mid_index:] #data[0:]-->[18] search(num,data) elif num < mid_value: #num在列表的左边 data=data[:mid_index] search(num,data) else: print('find it') return else: if data[0] == num: print('find it') else: print('not exists') search(19,data) # 查询 19 是否在列表中 ##输出结果 [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35] #总范围 [18, 20, 21, 22, 23, 30, 32, 33, 35] #总范围的一半 [18, 20, 21, 22] [18, 20] [18] not exists # 19 不在列表中
