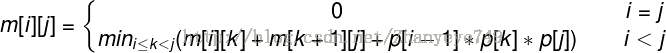矩阵连乘----动态规划

问题描述
　　有n个矩阵，大小分别为a0*a1, a1*a2, a2*a3, ..., a[n-1]*a[n]，现要将它们依次相乘，只能使用结合率，求最少需要多少次运算。
　　两个大小分别为p*q和q*r的矩阵相乘时的运算次数计为p*q*r。
输入格式
　　输入的第一行包含一个整数n，表示矩阵的个数。
　　第二行包含n+1个数，表示给定的矩阵。
输出格式
　　输出一个整数，表示最少的运算次数。
样例输入
3
1 10 5 20
样例输出
150
数据规模和约定

1<=n<=1000, 1<=ai<=10000。

----------------------------------------------------------------------------------------------(＾Ｕ＾)ノ~ＹＯ

为了说明在计算矩阵连乘积时计算次序对整个计算量的影响，我们来看一个计算3个矩阵{A1，A2，A3}的连乘积的例子。设这3个矩阵的维数分别为10×100，100×5和5×50。

若按第一种方式((A1A2)A3)来计算，需要10×100×5+10×5×50=7500次的数乘。

若按第二种方式(A1(A2A3))来计算，需要100×5×50+10×100×50=75000次的数乘。

由此可见，在计算矩阵连乘积时，计算次序对计算量有很大影响。

下面的参考连接是我找到最详细的，看完差不多就明白啦！！！

参考：http://blog.csdn.net/ljp1919/article/details/42610837

m[i][j]为第i个矩阵到第j个矩阵连乘的最小乘法数

#include <iostream>

using namespace std;

void MatrixChainOrder(int *p,int **m,int n)
{
    int l,i,j,k;  //l表示矩阵链的长度
    int q;

    for(int i=1; i<=n; i++)
    {
        m[i][i]=0;//m[i][i]只有一个矩阵，所以相乘次数为0，即m[i][i]=0
    }
    //l表示矩阵链的长度
	// l=2时，计算 m[i,i+1],i=1,2,...,n-1 (长度l=2的链的最小代价)
    for(l=2; l<=n; l++)
    {
        for(i=1; i<=n-l+1; i++) //
        {
            j=i+l-1;//以i为起始位置，j为长度为l的链的末位
            m[i][j]=0x7fffffff;
            //k从i到j-1,以k为位置划分
            for(k=i; k<=j-1; k++)
            {
                q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
                if(q<m[i][j])//寻找最小结果
                {
                    m[i][j]=q;
                }
            }
        }
    }
    cout<<m[1][n];
}

int main()
{
    int n;
    while(cin>>n)
    {
        int *p=new int[n+1];
        for(int i=0; i<=n; i++) //p为矩阵链
            cin>>p[i];

        int **m=new int*[n+1];  //m为存储最优结果的二维矩阵
        for(int i=0; i<=n; i++)
        {
            m[i]=new int[n+1];
        }
        MatrixChainOrder(p,m,n);
    }
    return 0;
}