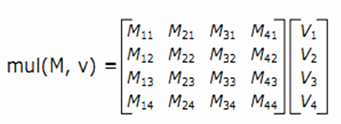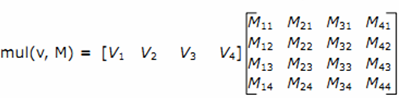数学类函数(Mathematical Functions)
|
abs(x) |
返回标量和向量x的绝对值 如果x是向量,则返回每一个成员的绝对值 |
|
acos(x) |
返回标量和向量x的反余弦 x的范围是[-1,1],返回值的范围是[0,π], 如果x是向量,则返回每一个成员的反余弦 |
|
all(x) |
如果一个布尔标量为真,或者布尔向量的所有成员为真,则返回真 |
|
any(x) |
如果一个布尔标量为真,或者布尔向量成员存在真值,则返回真 |
|
asin(x) |
返回标量和向量x的反正弦 x的范围是[-1,1],返回值的范围是[-π/2,π/2], 如果x是向量,则返回每一个成员的反正弦 |
|
atan(x) |
返回标量和向量x的反正切 x的范围不限,返回值的范围是[-π/2,π/2], 如果x是向量,则返回每一个成员的反正切· |
|
atan2(y, x) |
返回标量和向量y/x的反正切 返回值的范围是[-π,π], |
|
ceil(x) |
返回不小于x的下一个整数 |
|
clamp(x, a, b) |
返回一个[a, b]范围内的数 如果x<a则返回a 如果x>b则返回b 否则返回x |
|
cos(x) |
返回x的cos值 |
|
cosh(x) |
返回一个x的双曲线cos值 |
|
cross(a, b) |
返回a, b的叉积 a, b一定含有3个成员 |
|
degrees(x) |
弧度转化为角度 |
|
determinant(M) |
返回的正方形矩阵m的行列式 |
|
dot(a, b) |
返回a与b的点积 |
|
exp(x) |
返回以e为底的x次幂 |
|
exp2(x) |
返回以2为底的x次幂 |
|
floor(x) |
返回不大于x的上一个整数 |
|
fmod(x, y) |
返回一个x/y的余数, y如果为0,结果不可预料 |
|
frac(x) |
返回x的小数部分 |
|
frexp(x, out exp) |
将浮点数x分解为尾数(在[0.5, 1]范围内)和指数(输出为e) 如果x为0,结果的所有部分都为0 |
|
isfinite(x) |
如果x是有限的则返回true |
|
isinf(x) |
如果x是无限的则返回true |
|
isnan(x) |
NaN(not-a-number) 如果x NaN(not-a-number) 则返回true |
|
ldexp(x, n) |
x * 2的n次方 |
|
lerp(a, b, w) |
w是比重 当w= 0时返回a,当w= 1时返回b 根据w返回一个[a, b]的值 p.s. w可以为任意值,不用限制在[0, 1]之内 w can be any value (so is not restricted to be between zero and one); |
|
lit(ndotl, ndoth, m) |
计算环境、漫反射、和高光的光照系数 返回一个4维向量 x,环境光系数,经常值为1.0 y,漫反射系数 如果 dot(n, l) < 0返回0,否则返回dot(n, l) z,高光系数 如果 dot(n, l) < 0或dot(n, h) < 0返回0,否则返回dot(n, h)的m次方 w 固定值为1.0 |
|
log(x) |
ln(x) |
|
log2(x) |
以2为底x的对数 |
|
log10(x) |
以10为底x的对数 |
|
max(a, b) |
返回a,b中的最大值 |
|
min(a, b) |
返回a,b中的最小值 |
|
modf(x, out ip) |
把x分离成整数和小数部分,把x的整数值存在输出参数ip处,并返回x的小数部分 |
|
mul(M, N) |
矩阵M和N的乘积 如果M是一个AxB的矩阵,N是一个BxC的矩阵,就返回一个AxC的矩阵 |
|
mul(M, v) |
矩阵M和列矢量v的乘积 如果M是一个AxB的矩阵,v是一个Bx1的矢量,就返回一个Ax1的矢量 |
|
mul(v, M) |
行矢量v和矩阵M的乘积
如果v是一个1xA的矢量,M是一个AxB的矩阵,就返回一个1xB的矢量 |
|
noise(x) |
任意一个1维2维或3维的噪波函数取决于x的类型。 返回一个[0, 1]范围内的,总是和输入相同的值 |
|
pow(x, y) |
返回x的y次方值 |
|
radians(x) |
角度转化为弧度的值 |
|
round(x) |
采用四舍五入法,返回把x化为整数值 |
|
rsqrt(x) |
返回x的平方根的倒数 x必须大于0 |
|
saturate(x) |
返回一个[0, 1]范围内的数 如果x<0则返回0 如果x>1则返回1 否则返回x |
|
sign(x) |
如果 x>0返回1 如果 x<0返回-1 否则返回0 |
|
sin(x) |
返回x的sin值 |
|
sincos(float x, out s, out c) |
输出参数s 为x的sin值,c为s的cos值 这个函数比分别计算x的sin和cos有效率 此函数无返回值 |
|
sinh(x) |
返回一个x的双曲线sin值 |
|
smoothstep(min, max, x) |
x是一个[min, max]范围内的数 如果x=min返回0,如果x=max返回1 否则返回如下公式的计算结果: |
|
step(a, x) |
如果 x<a返回0 如果 x≥a返回1 |
|
sqrt(x) |
返回x的平方根 x必须大于0 |
|
tan(x) |
返回x的tan值 |
|
tanh(x) |
返回一个x的双曲线tan值 |
|
transpose(M) |
返回M的转置矩阵 |
cg函数的内部代码实施
看了他们的函数内部实现代码,感觉他们写的都很巧妙,可以用“微量高效”来形容,值得我们学习
abs(x)
如果x是float值,则内部是这么实施的
float abs(float a)
{
return max(-a, a);
}
操作消耗的非常小,等同于无
acos(x)
如果x是float值,则内部是这么实施的
// Handbook of Mathematical Functions
// M. Abramowitz and I.A. Stegun, Ed.
// Absolute error <= 6.7e-5
float acos(float x) {
float negate = float(x < 0);
x = abs(x);
float ret = -0.0187293;
ret = ret * x;
ret = ret + 0.0742610;
ret = ret * x;
ret = ret - 0.2121144;
ret = ret * x;
ret = ret + 1.5707288;
ret = ret * sqrt(1.0-x);
ret = ret - 2 * negate * ret;
return negate * 3.14159265358979 + ret;
}
all(x)
如果x是float值,则内部是这么实施的
bool all(bool4 a)
{
return a.x && a.y && a.z && a.w;
}
any(x)
如果x是float值,则内部是这么实施的
bool any(bool4 a)
{
return a.x || a.y || a.z || a.w;
}
asin(x)
如果x是float值,则内部是这么实施的
// Handbook of Mathematical Functions
// M. Abramowitz and I.A. Stegun, Ed.
float asin(float x) {
float negate = float(x < 0);
x = abs(x);
float ret = -0.0187293;
ret *= x;
ret += 0.0742610;
ret *= x;
ret -= 0.2121144;
ret *= x;
ret += 1.5707288;
ret = 3.14159265358979*0.5 - sqrt(1.0 - x)*ret;
return ret - 2 * negate * ret;
}
atan(x)
如果x是float值,则内部是这么实施的
float atan(float x) {
return atan2(x, float(1));
}
atan2(y, x)
float2 atan2(float2 y, float2 x)
{
float2 t0, t1, t2, t3, t4;
t3 = abs(x);
t1 = abs(y);
t0 = max(t3, t1);
t1 = min(t3, t1);
t3 = float(1) / t0;
t3 = t1 * t3;
t4 = t3 * t3;
t0 = - float(0.013480470);
t0 = t0 * t4 + float(0.057477314);
t0 = t0 * t4 - float(0.121239071);
t0 = t0 * t4 + float(0.195635925);
t0 = t0 * t4 - float(0.332994597);
t0 = t0 * t4 + float(0.999995630);
t3 = t0 * t3;
t3 = (abs(y) > abs(x)) ? float(1.570796327) - t3 : t3;
t3 = (x < 0) ? float(3.141592654) - t3 : t3;
t3 = (y < 0) ? -t3 : t3;
return t3;
}
ceil(x)
如果x是float值,则内部是这么实施的
float ceil(float v)
{
return -floor(-v);
}
clamp(x)
如果x是float值,则内部是这么实施的
float clamp(float x, float a, float b)
{
return max(a, min(b, x));
}
cos(x)
如果x是float值,则内部是这么实施的
cos(float a)
{
/* C simulation gives a max absolute error of less than 1.8e-7 */
const float4 c0 = float4( 0.0, 0.5,
1.0, 0.0 );
const float4 c1 = float4( 0.25, -9.0,
0.75, 0.159154943091 );
const float4 c2 = float4( 24.9808039603, -24.9808039603,
-60.1458091736, 60.1458091736 );
const float4 c3 = float4( 85.4537887573, -85.4537887573,
-64.9393539429, 64.9393539429 );
const float4 c4 = float4( 19.7392082214, -19.7392082214,
-1.0, 1.0 );
/* r0.x = cos(a) */
float3 r0, r1, r2;
r1.x = c1.w * a; // normalize input
r1.y = frac( r1.x ); // and extract fraction
r2.x = (float) ( r1.y < c1.x ); // range check: 0.0 to 0.25
r2.yz = (float2) ( r1.yy >= c1.yz ); // range check: 0.75 to 1.0
r2.y = dot( r2, c4.zwz ); // range check: 0.25 to 0.75
r0 = c0.xyz - r1.yyy; // range centering
r0 = r0 * r0;
r1 = c2.xyx * r0 + c2.zwz; // start power series
r1 = r1 * r0 + c3.xyx;
r1 = r1 * r0 + c3.zwz;
r1 = r1 * r0 + c4.xyx;
r1 = r1 * r0 + c4.zwz;
r0.x = dot( r1, -r2 ); // range extract
return r0.x;
cosh(x)
如果x是float值,则内部是这么实施的
float cosh(float x)
{
return 0.5 * (exp(x)+exp(-x));
}
degrees(x)
如果x是float值,则内部是这么实施的
float degrees(float a)
{
return 57.29577951 * a;
}
determinant (x)
float determinant(float1x1 A)
{
return A._m00;
}
float determinant(float2x2 A)
{
return A._m00*A._m11 - A._m01*A._m10;
}
float determinant(float3x3 A)
{
return dot(A._m00_m01_m02,
A._m11_m12_m10 * A._m22_m20_m21
- A._m12_m10_m11 * A._m21_m22_m20);
}
float determinant(float4x4 A) {
return dot(float4(1,-1,1,-1) * A._m00_m01_m02_m03,
A._m11_m12_m13_m10*( A._m22_m23_m20_m21*A._m33_m30_m31_m32
- A._m23_m20_m21_m22*A._m32_m33_m30_m31)
+ A._m12_m13_m10_m11*( A._m23_m20_m21_m22*A._m31_m32_m33_m30
- A._m21_m22_m23_m20*A._m33_m30_m31_m32)
+ A._m13_m10_m11_m12*( A._m21_m22_m23_m20*A._m32_m33_m30_m31
- A._m22_m23_m20_m21*A._m31_m32_m33_m30));
}
degrees(x)
如果x是float4值,则内部是这么实施的
float dot(float4 a, float4 b)
{
return a.x*b.x + a.y*b.y + a.z*b.z + a.w*b.w;
}
exp(x)
float3 exp(float3 a)
{
float3 rv;
int i;
for (i=0; i<3; i++) {
rv[i] = exp(a[i]); // this is the ANSI C standard library exp()
}
return rv;
}
exp2(x)
float3 exp2(float3 a)
{
float3 rv;
int i;
for (i=0; i<3; i++) {
rv[i] = exp2(a[i]); // this is the ANSI C standard library exp2()
}
return rv;
}
floor(x)
float3 floor(float3 v)
{
float3 rv;
int i;
for (i=0; i<3; i++) {
rv[i] = v[i] - frac(v[i]);
}
return rv;
}
fmod(x)
float2 fmod(float2 a, float2 b)
{
float2 c = frac(abs(a/b))*abs(b);
return (a < 0) ? -c : c; /* if ( a < 0 ) c = 0-c */
}
frac(x)
float frac(float v)
{
return v - floor(v);
}
frexp(x)
float3 frexp(float3 x, out float3 e)
{
float3 rv;
int i;
for (i=0; i<3; i++) {
float eout;
rv[i] = frexp(a[i], &eout); // this is the ANSI C standard library frexp()
e[i] = eout;
}
return rv;
}
isfinite(x)
bool3 isfinite(float3 s)
{
// By IEEE 754 rule, 2*Inf equals Inf
return (s == s) && ((s == 0) || (s != 2*s));
}
isinf(x)
bool3 isinf(float3 s)
{
// By IEEE 754 rule, 2*Inf equals Inf
return (2*s == s) && (s != 0);
}
isnan(x)
bool3 isnan(float3 s)
{
// By IEEE 754 rule, NaN is not equal to NaN
return s != s;
}
lerp(a, b, f)
float3 lerp(float3 a, float3 b, float w)
{
return a + w*(b-a);
}
lit(ndotl, ndoth, m)
float4 lit(float NdotL, float NdotH, float m)
{
float specular = (NdotL > 0) ? pow(max(0.0, NdotH), m);
return float4(1.0, max(0.0, NdotL), specular, 1.0);
}
max(a, b)
float3 max(float3 a, float3 b)
{
return float3(a.x > b.x ? a.x : b.x,
a.y > b.y ? a.y : b.y,
a.z > b.z ? a.z : b.z);
}
min(a, b)
float3 min(float3 a, float3 b)
{
return float3(a.x < b.x ? a.x : b.x,
a.y < b.y ? a.y : b.y,
a.z < b.z ? a.z : b.z);
}
modf(x, out ip)
float4 mul(float4x3 M, float3 v)
{
float4 r;
r.x = dot( M._m00_m01_m02, v );
r.y = dot( M._m10_m11_m12, v );
r.z = dot( M._m20_m21_m22, v );
r.w = dot( M._m30_m31_m32, v );
return r;
}
pow(x, y)
float3 pow(float3 x, float3 y)
{
float3 rv;
for (int i=0; i<3; i++) {
rv[i] = exp(x[i] * log(y[i]));
}
return rv;
}
round(x)
// round-to-nearest even profiles
float round(float a)
{
float x = a + 0.5;
float f = floor(x);
float r;
if (x == f) {
if (a > 0)
r = f - fmod(f, 2);
else
r = f + fmod(f, 2);
} else
r = f;
return r;
}
// round-to-nearest up profiles
float round(float a)
{
return floor(x + 0.5);
}
rsqrt(x)
float3 rsqrt(float3 a)
{
return pow(a, -0.5);
}
saturate(x)
float saturate(float x)
{
return max(0, min(1, x));
}
sign(x)
float3 sign(float x)
{
float3 val = a > 0;
return val - (a < 0);
}
step(a, x)
float3 step(float3 a, float3 x)
{
return x >= a;
}
sqrt(x)
感觉这个有点麻烦了,直接pow就好了。
float3 sqrt(float3 a)
{
return 1.0 / rsqrt(a);
}
transpose(M)
float4x3 transpose(float3x4 A)
{
float4x3 C;
C[0] = A._m00_m10_m20;
C[1] = A._m01_m11_m21;
C[2] = A._m02_m12_m22;
C[3] = A._m03_m13_m23;
return C;
}
------------------------------------by wolf96 http://blog.csdn.net/wolf96