刚进实验室,被叫去看CNN。看了一些博客和论文,消化了很久,同时觉得一些博客存在一些谬误。我在这里便尽量更正,并加入自己的思考。如果觉得本文有哪里不妥或疑惑,请在下面发表评论,大家一起探讨。如有大神路过,请务必教我做人。然后,那些捣乱的,泥垢,前面左转不送。
卷积神经网络(CNN)是deep learning的基础。传统的全连接神经网络(fully connected networks) 以数值作为输入。如果要处理图像相关的信息的话,要另外从图像中提取特征并采样。而CNN把提特征、下采样和传统的神经网络整合起来,形成一个新的网络。本文假设你已经有了简单神经网络的概念,如“层(layers)”、“神经元(neurons)”。
一. 理论基础
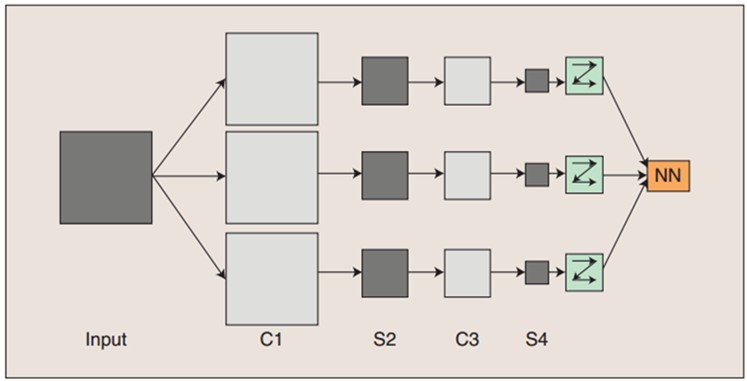
图1
Α. 简单网络拓扑:
如图1所示,这是一个简单的卷积神经网络 CNN。其中C层代表对输入图像进行滤波后得到的所有组成的层,也称“卷积层”。S层代表对输入图像进行下采样(subsampling)得到的层。其中C1和C3是卷积层 ,S2和S4则是下采样层。C、S层中的每一层都由多个二维平面组成,每一个二维平面是一个特征图 (feature map)。
以图1所示的CNN为例,讲讲图像的处理流程:
图像输入网络后,通过三个滤波器(filter) 进行卷积,得到C1层的三个特征图(feature map)。C1层的三个特征图分别通过下采样得到S2层的三个特征图。这三个特征图通过一个滤波器卷积得到C3层的三个特征图,然后和前面类似,下采样得到S4层的三个特征图。最后,S4层的特征图光柵化后,变成向量。这个向量输入到传统的全连接神经网络(fully connected networks)中进行进一步的分类。
图中的C1、S2 、C3、S4层中的所有特征图都可以用 “像素 x 像素” 定义图像大小。你会说,图像的大小不就是用像素x像素定义的么? 没错,但这里有点特殊,由于这些特征图组成了神经网络的卷积层和下采样层,而在神经网络(neural networks)中,每一层都有“神经元” (neurons) 的概念。这些特征图中的每一个像素恰恰旧就代表了一个神经元。每一层所有特征图的像素个数,就是当层网络的神经元个数,这是可以算出来的,怎么算? 再往后面看一看。
Β. 隐层(hidden layer):
提到了神经元的概念之后,就可以讲述 a) CNN中C-S部分的隐层(NN部分的隐层就不在这里讲了) 还有 b) 层与层之间,神经元的连接情况的概念了。隐层就是一块黑色的面纱,它隐藏了真相,但种种蛛丝马迹(如滤波器的大小、步长,下采样的范围,偏置数等等)告诉你,你已经很逼近真相了。嗯,不扯了,就是说有了那些东西,你就可以算出神经元的数目、可学习的参数个数、神经元的连接数了。分为两种:别的层和卷积层之间的隐层、卷积层和下采样层之间的隐层。
1. 别的层和卷积层之间的隐层:
滤波器(卷积核)的定义: 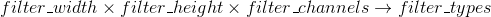
filter_width、filter_height → 滤波范围的宽、高;filter_channels → 过滤图像的通道数;filter_types → 滤波器的种类。
如 5x5x3 → 20: 滤波器宽高各为5个像素,卷积通道数为3,共20种
下面会涉及局部感受野的概念和权值共享
一般来说,如果C层中的所有神经元都和输入图像上的每一个像素点建立连接,那么这个连接数目是极其庞大的。需要学习的参数个数也另人瞠目结舌。
举个例子,若输入图像大小为 200x200,C1层由6个特征图,每个特征图大小为20x20(神经元数目为20x20=400个)。并且,使滤波器为10x10的单通道滤波器(channel = 1),且步长为10---相当于相邻的两个滤波区域恰好不重叠,这样便于计算啦。 那么总共的连接数目是 200x200x(6x20x20) = 96000000。天哪,九千多万个连接,如果每个连接一个参数的话,那就九千多万的可训练参数(learnable parameters),如此复杂的网络,根本就没有计算的可能,地球都毁灭了,参数还没训练好。。。
在我们的生活中。看见一样东西,通常都是先看到它的局部,一般不会一下就能看到一件物品的全部内容。这就是局部感受野,CNN用了这个策略。卷积层中的除了可加偏置之外,每一个神经元都只和输入图像中的一个局部区域中的像素点相连接。(此局部区域的大小就是滤波器的宽高积)
C层的一个特征图(feature map) 是输入图像通过一种滤波器(filter) 得到的。假设这中滤波器提取 “T” 特征。特征图上面的每一个神经元都通过这个滤波器和原图像上面自己对应的那个局部区域相关联(和局部区域中的像素点相连)。这样一来啊,每个神经元获得了自己对应区域的 T 特征后,把大家的那份都整起来,不就相当于获得原图的 T 特征了吗 ?
让我们来算算,现在连接的数目是多少!每个神经元只和一个10x10的区域相连,那就是 10x10x(6x20x20) = 240000。现在最多只有24w个可训练参数了。 还可以减少 !
ps: 每一个神经元都对应一个值,这个值由它指向的原图的区域里的所有像素点值通过滤波器卷积算出。
下面,谈谈权值共享。我们已经知道,输入图像通过一种滤波器卷积得到一张特征图。特征图上的每个神经元都与原图上的一个矩形滤波区域上的像素点连接,上例就是10x10。辣么每一神经元和原图上的10x10个输入神经元有连接。由于这些神经元想要的是同一种特征,所以它们通过同一个滤波器来滤波。因此,每一个神经元上的这10x10的连接上的参数是 一毛一样的。 是不是很有道理的样子 ? 实际上,这10x10个参数被这张特征图上的所有神经元共享。这就是权值共享啊! 那么即使6张特征图,也只有6x10x10 = 600 个需要训练的参数。(假设输入层只有一张图)
进一步地,这10x10的参数仿佛只和滤波有关,就像是6个滤波器,每个都自带100个参数一样。而且这些参数需要训练。就像是自学习的滤波器一样!
e.g. 有一个5x5x3 → 20的滤波器,输入一个原始图像,通过卷积得到C层的20个特征图。
可训练参数 = (5x5x3 + 1) x 20 = 1520个
每张特征图上神经元的数目和 输入图的宽高、滤波器的宽高、滤波器的步长(stride)均有关,且等于原图上可取的滤波区域的数目。上面我们给出的例子里面由于滤波器的宽高为10x10且步长为10,所以没有两个滤波区域是重叠的,比较理想。一般情况下,就需要按下面的公式来算。设特征图的宽高分别是 n 和 m。
 ,
, 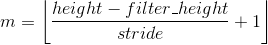 (1)
(1)
推导过程很简单,主要思想就是最右/下面的一个可放置滤波器的地方,就是最右/下面的滤波区域的右/下边界,不超过输入图像的width/height。列出下面两组不等式,解之即可得到 (1)。
 ,
,  (2)
(2)
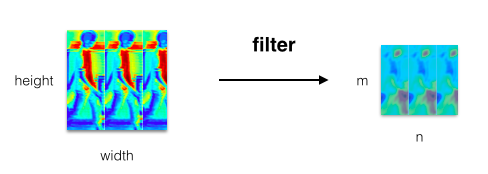
图2
如果输入的这个层(指的是输入给C层的那个层,不只是指最开始的Input层)的图像只有一个特征图,那么隐层的参数个数可以简单地这样计算--隐层可训练参数个数 = (滤波器大小 + 可加偏置数目) x 滤波器种类。如果不是,情况就会不同,因为原来当输入层只有一个图的时候,C层的神经元都指向输入层的那个图的一个区域。如果输入层有P个图(P > 1),特别是当C层的特征图的数目Q和P不同的时候,分配不均,C层的神经元就会指向输入层的R个图的R个区域了(R ≤ P)。这里可以有多种分配策略,比如一个特征图上的神经元指向输入层三个图的区域啦,又一个特征图上的神经元指向输入层六个图的区域啦,这直接就影响到参数的计算了。具体策略具体算。文章最后面算LeNet-5参数的时候,会出现这样的情况,后面的例子会说明。
特征图的数目 = 滤波器的种类
隐层可训练参数个数: 1. 输入层只有一个特征图: (滤波器大小 + 可加偏置数) x 滤波器种类
I. 滤波器大小 = filter_width x filter_height x filter_channels
II. 可加偏置数,一般为1
2. 输入层不只一个特征图: 视具体情况而定
隐层可训练参数个数 = (滤波器大小 + 可加偏置数目) x 滤波器种类
卷积层上的神经元总数 = 特征图数目 x 可放置滤波器数目 = 特征图数目 x n x m
连接数 = 神经元总数 x 神经元所连接的输入图像的局部区域大小
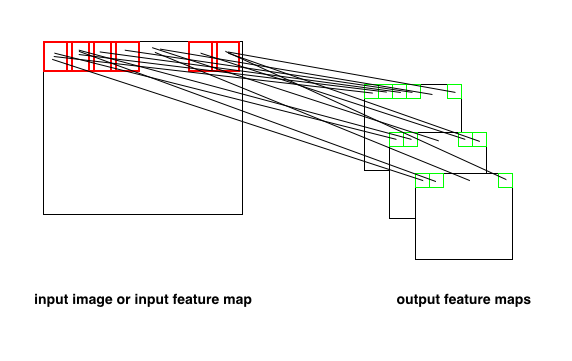
图3
如图3所示,输出的特征图中的每一个神经元 (绿色小框),都指向输入图像的唯一的一个滤波区域(红色小框)。人懒,只画出了第一行。
可以看到红色的小框,即合法的滤波区域之间是有重叠(overlapping)的,这是故意的,因为允许设置滤波器在输入图像上的移动步长。而且最后一个红框离输入图像的右边缘有一小段距离,还是故意的,因为这可能是最右一个合法的滤波区域了。再往右按步长偏移放红框,这个框的右边界就超出输入图像的右边界了。同理,滤波器往下的情况也是类似的。
最后,你会发现,每一张特征图上的神经元个数就是输入图像的合法滤波区域个数。虽然,上面看好像每个神经元只有一条线指向区域,但是,实际上,这条线上有filter_width x filter_height 个连接。令 k = filter_width x filter_height,如果还加上一个可加偏置,那么一个神经元上面就有(k+1)个参数了。一张feature map上的所有神经元共享这k+1个参数。像图3有三个特征图,那么上图3的隐层参数总数就是3k+3。
2. 卷积层和下采样层之间的隐层:
为啥需要下采样,因为虽然在得到卷积层的时候,我们使用了一些策略比如 “局部感受野”、“权值共享” 使得计算量大为减少。但是得到的图像信息可能仍然很多。下采样取样一般是减半(halve),通过把输入的卷积层中的每个特征图上的2x2的区域的4个像素点值加起来,乘一个权值w,再加上一个偏置b,最后通过一个sigmoid函数得到S层的一个像素点(神经元)的值。在每一张feature map中,w和b是被其上的所有神经元共享的,也是唯一需要学习的参数。把一个2x2的区域浓缩成一个值,相当于总结出一个更高层的特征。还有,每个2x2的采样区域不重合。
由于下采样层S的特征图相当于C层的特征图宽高都减半,但毕竟C层的特征图的宽高可能是奇数啊。
为了不损失数据,可能会生成一些数据来弥补,如果缺失两个格子,再copy一份即可。 如果是有地方只采到一个格子呢 ? 涉及到一些小策略。
简单粗暴,用最直接的公式:
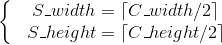 (3)
(3)
那么下采样层的神经元总数 = 总像素点个数 = 特征图数目 x S_width x S_height
隐层可训练参数个数 = 特征图数目 x (1+1) = 特征图数目 x 2 (1+1 是一个w加一个b)
那么连接数是怎么计算的呢? 前面说过了,卷积层的2x2区域的4个像素加起来乘以一个w再加上b就得到下采样层的一个神经元的值. 那么这个神经元实际上有5个连接出去。为什么? 和4个像素的各有一个连接(四个连接上面的参数都是同一个w),和可加偏置b有一个连接,共5个连接。
所以连接数 = 神经元总数 x (2x2+1) = 神经元总数 x 5
下采样不改变特征图的数目
隐层可训练参数个数 = 特征图数目 x 2
下采样层的神经元总数= 特征图数目 x S_width x S_height
连接数 = 神经元总数 x 5
二. 计算实践
下面以Yann LeCun的手写数字识别CNN “LeNet-5” 为例,算算里面的一些参数:
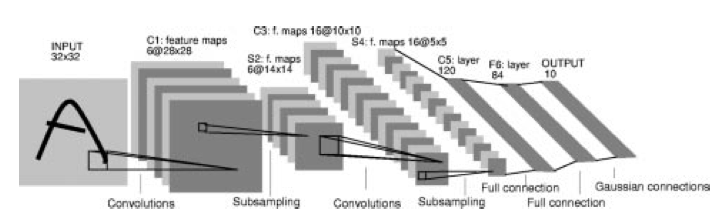
图4
LeNet-5的网络结构:Input-C1-S2-C3-S4-C5-F6
Input-C1:
这之间有个单通道滤波器 5x5x1 → 6,stride = 5。滤波器大小为 5x5x1 = 25,有一个可加偏置,6中滤波器得到C1的6个特征图。按照我在上面给出的公式,可以算出:
可训练参数 = (5x5x1 + 1) x 6 = 156
C1一层特征图神经元的总数 = floor( (32-5)/1 +1 ) x floor( (32-5)/1 + 1) = 28x28,也是C1特征图的大小。
总神经元的个数 = 28x28x6
每个神经元的的连接数 = 5x5 + 1 (5x5的滤波区域 + 1个可加bias)
总连接数 = 28x28x6x(5x5+1) = 122,304个
另外,不要把滤波区域(filter_width x filter_height) 和 滤波器的大小(filter_width x filter_height x filer_channels) 搞混了。在这个例子中“5x5” 和 “5x5x1” 很不一样。
C1-S2:
可训练参数 = 6 x (1+1) = 12个 (6个特征图 x (1个w+1个b))
S2一层特征图神经元的总数 = ceiling(28/2) x ceiling(28/2) = 14x14,也是S2特征图的大小
总神经元的个数 = 14x14x6个
每个神经元的连接数 = 2x2 + 1 (2x2的采样区域+1个可加bias)
总连接数 = 14x14x6x(2x2 + 1) = 5,880个
S2-C3:
看着图4,发现S2层的6个特征图,卷积得到了C3层的16个特征图。这里用到的策略是组合。首先,我们要把S2层的6个特征图看成是首尾相连的。
那么3个相邻的特征图组合的组合数是6,4个相邻的特征图组合的组合数也是6,4个不全相邻的特征图组合的组合数是9。然后就是会有C3层的特征图上的神经元指向S2层的多个特征图的区域的情况出现。
譬如,一种分配情况: C3的前6个特征图以S2中3个相邻的特征图集合为输入,接下来的6个特征图以S2中4个相邻的特征图集合为输入,再有3个特征图以不全相邻的4个特征图子集(从9个里面挑3个出来)为输入,最后一个特征图以S2中所有特征图作为输入。且滤波器为 5x5x1 → 10,stride = 1。
这样,需要训练的参数总数 = (5x5x1x3 + 1) x 6 + (5x5x1x4 + 1) x 6 + (5x5x1x4 + 1) x 3 + (5x5x1x6 + 1) x 1 = 1,516
计算的过程很简单,比如说第1项: (5x5x1x3 + 1) x 6 的意思就是前6个特征图中的一个,它上面的神经元,指向S2里的三个特征图的5x5区域,再加上一个偏置,一张特征图的神经元共享权值。所以一张图有 (5x5x1x3 + 1)个参数,然后总共有6个类似但不一样(连接的S2的特征图不全一样,所以参数不一样)的图。
C3的神经元总数 = 16 x ( floor( (14-5)/1 + 1) x floor( (14-5)/1 + 1) ) = 1,600个
连接数 = (5x5x1x3+1)x100x6 + (5x5x1x4+1)x100x6 + (5x5x1x4+1)x100x3 + (5x5x1x6+1)x100x1 = 151,600个
为啥上面的每一项里面都有一个 “x1”呢,因为滤波器的大小不只是宽高,还要乘以通道数。实际上你要把卷积核看成是立体的,只是在LeNet-5里面用的都是单通道滤波器,所以厚度为1而已。至于为什么要用16个卷积核,是经过实验验证比较合适 ?
C3-S4:
可训练参数 = (1+1) x 16 = 32个
S4一层特征图神经元的总数 = ceiling(10/2) x ceiling(10/2) = 5x5,也是S4特征图的大小
总神经元的个数 = 25x16 = 400个
每个神经元的连接数 = 2x2 + 1 = 5个 (2x2的采样区域 + 1个可加bias)
总连接数 = 400 x 5 = 2,000个
S4-C5:
S4-C5层的滤波器为 5x5x1 → 120,所以C5层有120个特征图。每个特征图的大小为 floor( (5-5)/1 + 1) x floor( (5-5)/1 + 1) = 1x1。每个特征图只有1个神经元。由于滤波区域的大小是5x5,这刚好是S4层的特征图的大小。相当于说,一个C5的特征图和它所连接的S4的特征图为全连接。而且,在LeNet-5中,C5中的特征图是指向S4所有的特征图的。相当于说,C5的每一个神经元,和S4层上的每一个像素点都连接了。
由于不同特征图是不会共享权值的,所以可训练参数个数 = 连接数 = (5x5x1x16 + 1) x 120 = 48,120个
C5层神经元的总数: 120个
C5-F6:
F6层有84个单元,C5和F6也是全连接的,同样地: 可训练参数个数 = 连接数 = (120 + 1) x 84 = 10,164个
接下来就是传统的神经网络了。至于后面的NN部分做了什么,怎么做,在引用文献的论文,或者链接博客的末尾也有讲述。目前,我对部分不太了解。好好学习吧。
关于pooling
还记得上面网络里边的下采样层S吗,就是用pooling技术把一个输入图的2x2区域里的值,通过一些方法(加权,求平均,求最大)来得到S层的一个神经元的值。pooling就是所谓“池化”,把四个像素点的值以一定比例像调鸡尾酒一样勾勾兑兑,弄出一个新值来,最多再加一个偏置,就得到一杯新酒了。常见的pooling策略有 max-pooling、mean-pooling、stochastic-pooling三种。max-pooling就是从4个值里边选最大的那个,mean-pooling就是取平均、stochastic-pooling就是按照某种“重要性”的原则,4个点分别乘以不同的权值。
pooling很直观的一个目的就是为了减少参数。除此之外,还能保证一定的不变性(invariance)。不变性包括 1) 平移不变性 2) 旋转不变性 3) 伸缩不变性。普遍认同的是能保证小范围的平移不变性,后面两种存在争议,让人感觉很随机 ? 再回去看三种pooling策略,前面两个极其简单粗暴,令人震惊。最后一个虽然比前面两个温和很多,但是权重的设置怎么搞 ? 还是忒不靠谱。看到知乎上有人说—前面两种pooling策略在参考文献[2]中有详细的分析。不过我很累,我想睡觉。[1]和[2]我都上传了,方便诸位下载。
References:
[1] Y. LeCun,L. Bottou,Y.Bengio,and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE,1998. 2
[2] Boureau, Y.-L; Bach,F.; LeCun, Y:; Ponce, J. Learning mid-level features for recognition. In CVPR, 2010.