| 博客班级 | 班级链接 |
|---|---|
| 作业要求 | 作业链接 |
| 学号 | 3180701119 |
| 实验一 感知器及其应用 |
【实验目的】
-
理解感知器算法原理,能实现感知器算法;
-
掌握机器学习算法的度量指标;
-
掌握最小二乘法进行参数估计基本原理;
-
针对特定应用场景及数据,能构建感知器模型并进行预测。
【实验内容】
-
安装Pycharm,注册学生版。
-
安装常见的机器学习库,如Scipy、Numpy、Pandas、Matplotlib,sklearn等。
-
编程实现感知器算法。
-
熟悉iris数据集,并能使用感知器算法对该数据集构建模型并应用。
【实验过程及结果】
源代码
1.
import pandas as pd #导入模块
import numpy as np
from sklearn.datasets import load_iris#引用sklearn.datasets模块的一部分
import matplotlib.pyplot as plt
%matplotlib inline#将matplotilb#绘制的图像显示在页面里,而不是弹出一个窗口
load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)#DataFram是pandas中一种默认的数据结构
df['label'] = iris.target#增加一列为类别标签
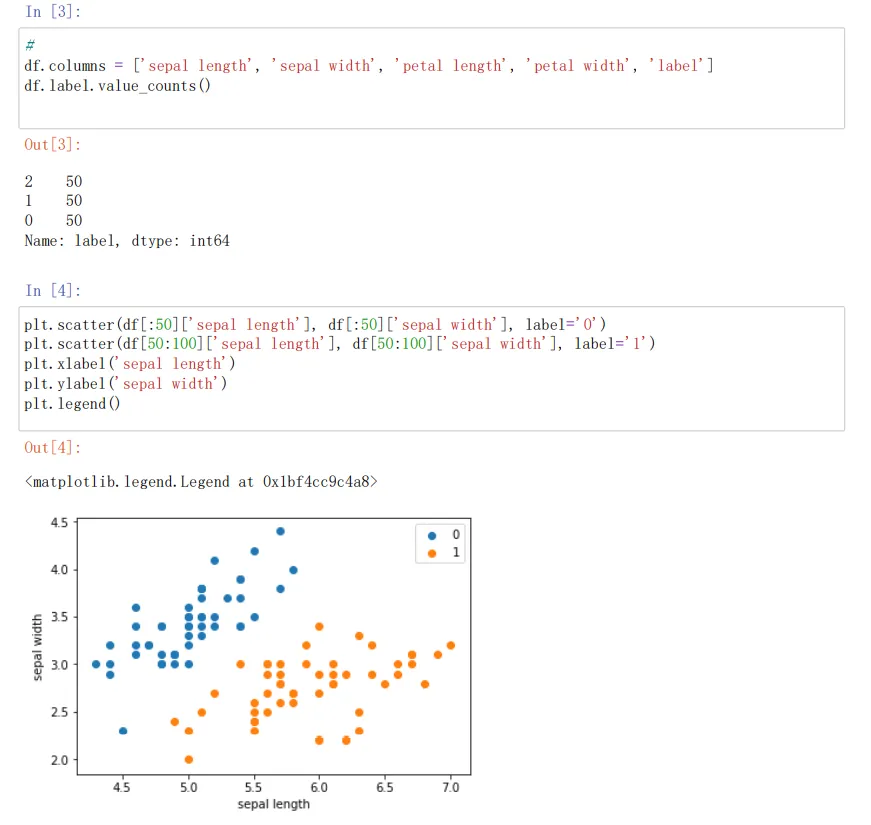
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']#返回给定DataFram类型的数据
df.label.value_counts()#value_counts确认数据出现的频率
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')#画散点图
plt.xlabel('sepal length')#x轴标签
plt.ylabel('sepal width')
plt.legend()#设置图标
data = np.array(df.iloc[:100, [0, 1, -1]]))#按行索引,取出第0,1,-1列
X, y = data[:,:-1], data[:,-1]#X为sepal length,sepal width y为标签
y = np.array([1 if i == 1 else -1 for i in y])
数据线性可分,二分类数据
此处为一元一次线性方程
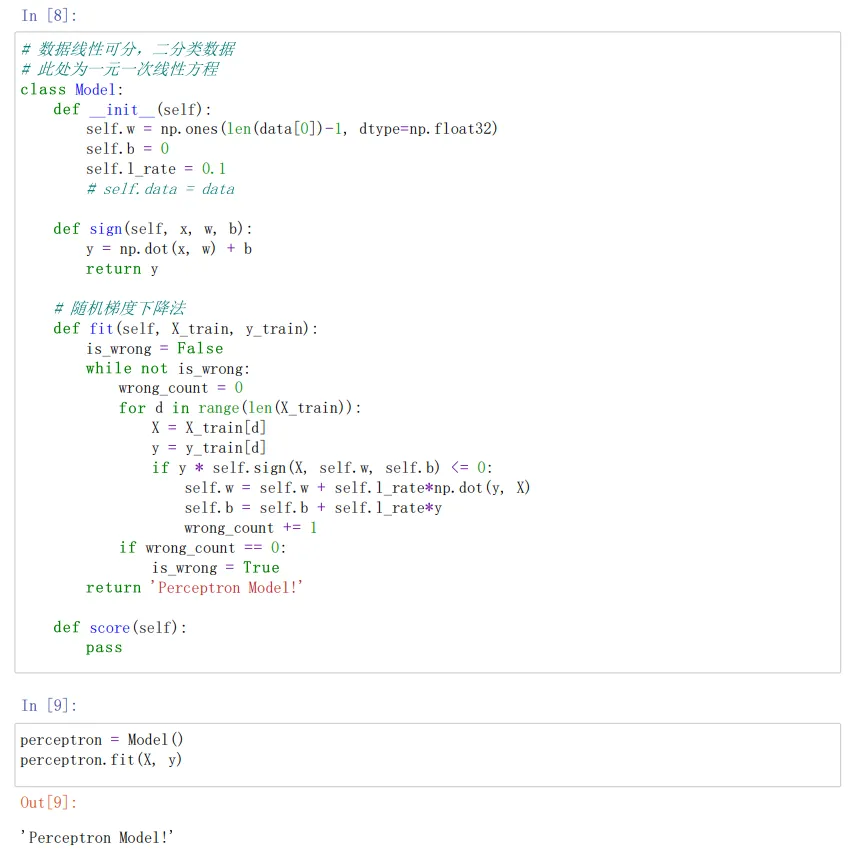
class Model:
def init(self):#将参数w1,w2置为1 b置为0 学习率为0.1
self.w = np.ones(len(data[0])-1, dtype=np.float32) data[0]#为第一行的数据len(data[0]=3)这里取两个w权重参数
self.b = 0
self.l_rate = 0.1
self.data = data
def sign(self, x, w, b):
y = np.dot(x, w) + b
return y
随机梯度下降法
def fit(self, X_train, y_train):#拟合训练数据求w和b
is_wrong = False#判断是否误分类
while not is_wrong:
wrong_count = 0
for d in range(len(X_train)):#取出样例,不断的迭代
X = X_train[d]
y = y_train[d]
if y * self.sign(X, self.w, self.b) <= 0:#根据错误的样本点不断的更新和迭代w和b的值(根据相乘结果是否为负来判断是否出错,本题将0也归为错误)
self.w = self.w + self.l_ratenp.dot(y, X)
self.b = self.b + self.l_ratey
wrong_count += 1
if wrong_count == 0:#直到误分类点为0 跳出循环
is_wrong = True
return 'Perceptron Model!'
def score(self):
pass
perceptron = Model()
perceptron.fit(X, y)#感知机模型
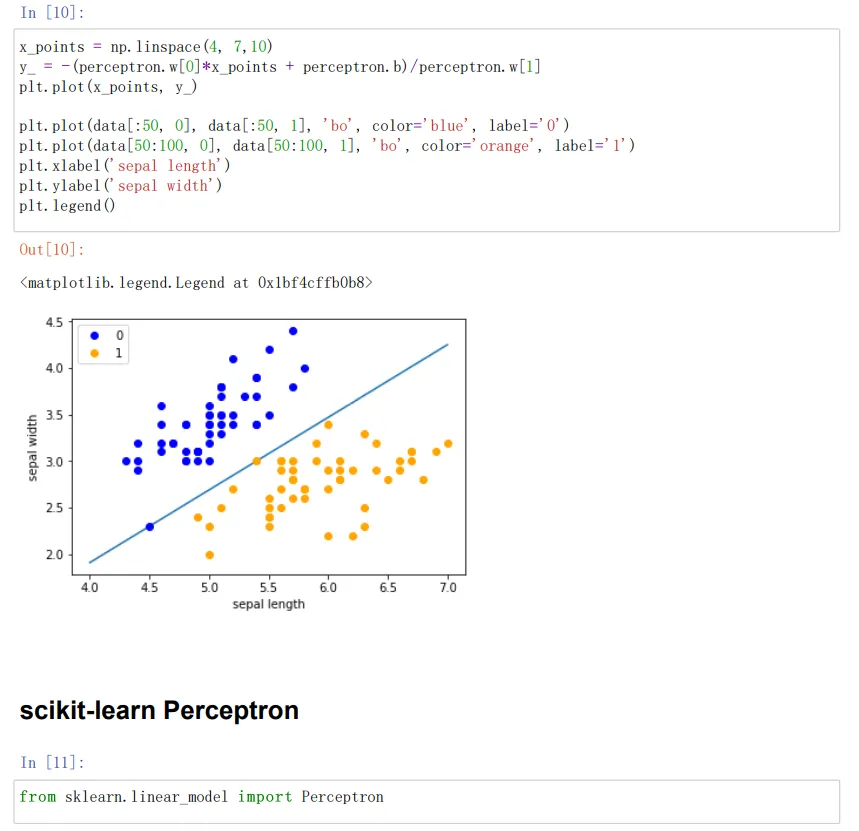
x_points = np.linspace(4, 7,10)#默认linspace函数可以生成元素为50的等间隔数列。而前两个参数分别是数列的开头与结尾。如果写入第三个参数,可以制定数列的元素个数。
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)#绘制模型图像(数据、颜色、图例等信息)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
from sklearn.linear_model import Perceptron#定义感知机(下面将使用感知机)
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
clf.fit(X, y)#使用训练数据拟合
Weights assigned to the features,输出感知机模型参数
print(clf.coef_)
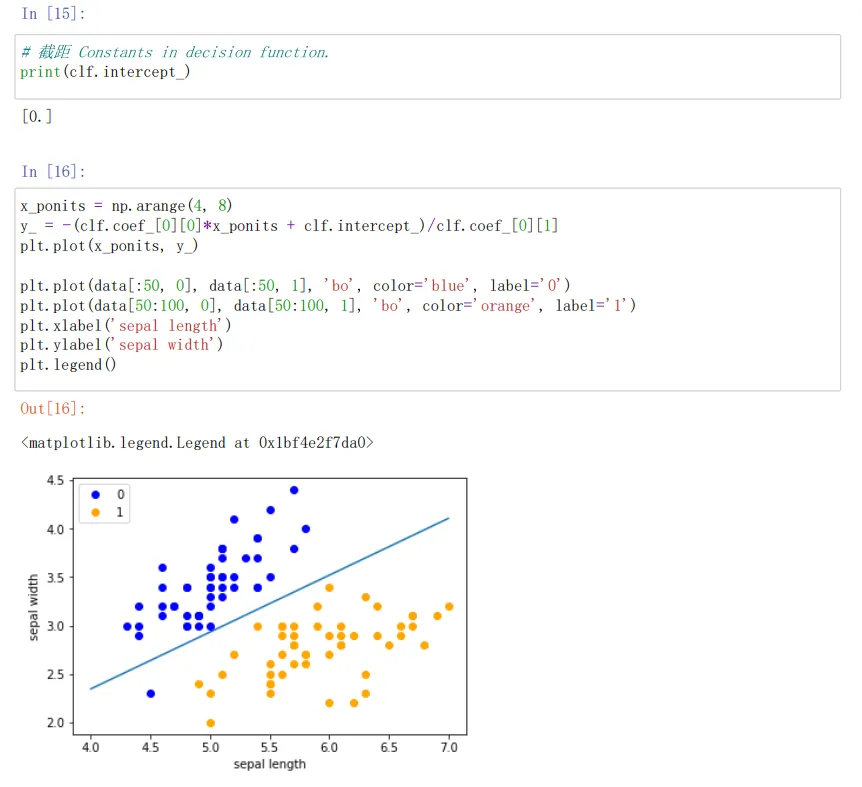
截距 Constants in decision function,输出感知机模型参数
print(clf.intercept_)
x_ponits = np.arange(4, 8)#确定x轴和y轴的值
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)#确定拟合的图像的具体信息(数据点,线,大小,粗细颜色等内容)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
实验结果