并行算法设计基础

并行算法的一般概念

并行算法的定义

• 并行算法是适合于在各种并行计算机上求解问题和处理数据的算法。它是一些可同时执行的诸进程的集合，这些进程相互作用和协调动作从而达到对给定问题的求解。

并行算法分类

• 数值计算：基于关系的一类运算。如矩阵运算，多项式求解。
• 非数值计算：基于比较关系的一类运算。如排序、选择、搜索、匹配、图论。
• 同步运算：某些进程必须等待别的进程（结果）的一类运算。
• 异步运算：某些进程的执行不必等待别的进程（结果）的一类运算。
• 有效并行算法：并行算法相对串行算法在性能（效率）方面，器时间关系具有对数特征，则这种并行算法是有效并行算法。

算法表达

• 一般采用形式化描述的方法，不提倡使用具体语言描述。
• 使用的关系词要配对，具有层次感。

算法分析

• 一般考虑的是算法的时空复杂度呈现最坏情况下的算法复杂度（即worst-case-complexity）
• 在MIMD计算模型上的并行算法的参量有：运行时间t(n)：在给定的模型上求解问题规模为n的给定问题所需时间，包括：①计算时间t_c在某一处理器执行算/逻运算所需时间。②选路时间t_r数据从原处理机到目的处理机所需时间。　　处理机数p(n)：求解给定问题所需的处理机数。
• 在MIMD计算模型上的并行算法的参量有：通信复杂度：算法在整个执行期间能传送的报文总数。时间复杂度：算法以第一台处理机开始执行到最后一台处理机执行中止所需时间。
• 界：①上界：令f(n)和g(n)是定义在自然数集合N上的两个函数，如果存在两个正的常数c和n₀，使得对于所有n≥n₀，均有f(n)≤c*g(n)，则称g(n)是f(n)的一个上界，记为f(n)=O(g(n))。②下界：令f(n)和g(n)是定义在自然数集合N上的两个函数，如果存在两个正的常数c和n₀，使得对于所有n≥n₀，均有f(n)≥c*g(n)，则称g(n)是f(n)的一个下界，记为f(n)=Ω(g(n))。③精确界：：令f(n)和g(n)是定义在自然数集合N上的两个函数，如果存在正的常数c₁，c₂和n₀，使得对于所有n≥n₀，均有c₁*g(n)≤f(n)≤c₂*g(n)，则称g(n)是f(n)的一个精确界，记为f(n)=Θ(g(n))。

算法指标

算法开销

• 并行算法运行时间t_p(n)与其所需处理器数量p(n)的乘积，即t_p(n)*p(n)
• 如果t_s(n)=t_p(n)*p(n)=串行计算的步数（节拍数）则算法称为最优

加速比

• Sp(n)=(最快的串行算法最坏的运行时间)/(并行算法最坏的运行时间)=t_s(n)/t_p(n)
• 一般有：t_s(n)≤p(n)*t_p(n)（通信、同步开销）；1≤Sp(n)≤p(n)

效率

• Ep(n)=Sp(n)/p(n)（加速比/处理机数）
• 一般有：0<Ep(n)≤1

并行计算模型

PRAM：SIMD-SM

基本概念

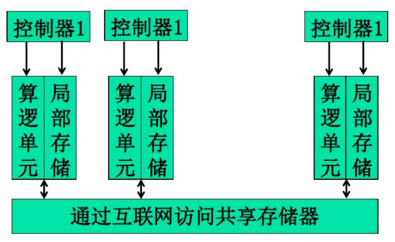
• PRAM（并行随机访问机器）模型也称为SIMD-SM模型，用于细粒度并行计算
• 采用集中式共享存储器模式，单一的编程访问空间
• 隐式同步机制

优点

• 适于表示和分析并行计算的复杂性
• 隐匿了并行计算机的大部底层细节（如通信、同步），从而易于使用

缺点

• 不适于MIMD计算机，存在存储器竞争和通信延迟问题

模型图示

APRAM：MIMD-SM

基本概念

• APRAM模型也称为分段（phase）PRAM模型；
• 用于中粒度的并行计算
• 采用集中式共享存储器，单一的访问地址空间
• （进程间）异步操作，但读/写共享变量操作采用显示同步方式

计算模式

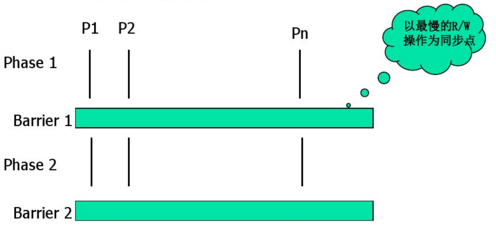
• 计算由若干个用同步点（barrier）划分的段组成
• 每一段异步运行局部程序
• 读/写操作在同步点进行同步

优点

• 保存了PRAM的简单性
• 可编程性和可调试性（correctness）好
• 易于进行程序复杂性分析

缺点

• 不适于具有分布式存储器的MIMD计算机

计算模式图示

模型图示

BSP：MIMD-DM

基本概念

• BSP模型是一种分布式存储器的多处理机模型，又称大同步模型
• 用于中大粒度并行计算
• （进程间）异步操作
• 采用报文发送和接收的通信方式进行显示同步

参数和计算模式

• BSP把并行计算机抽象为3个参数：P（处理机），g（宽带因子）和l（同步间隔）
• 计算由同步点（barrier）划分为若干个Supersteps
• 每个Superstep中实现异步的局部计算
• 在同步点通过发送和接收h-message进行同步

优点

• 把计算和通信分割开来
• 使用hashing自动进行存储器和通信管理
• 提供了一个编程环境

缺点

• 显式的同步机制限制并行计算机数据的增加
• 在一个Superstep中最多只能传递h个报文

BSP编程模式

BSP的开销

• C_superstep=maxW_i+maxH_ig+L
• process最大延迟时间
• W_i-进程pi的局部计算时间
• H_i-进程pi发送和接收的最大包数
• g-1/带宽（timestep/packet）（吞吐量 带宽因子）
• L-同步点同步时间间隔（同步点个数）
• 这里如果g=l=1，则BSP=PRAM-SIMD
• S=1-›带宽因子，吞吐率100%
• L=1-›若1个时间间隔为1个时间单位，则为1个同步点

LogP：MIMD-DM

基本概念

• LogP模型是技术趋势，编程经验和现行理论的综合产物
• 用于大粒度并行计算
• 使用分布式存储器的单一的和多重访问地址空间
• 进程间异步操作
• 采用报文通信方式隐式实现同步操作，即子集同步

参数和计算

• LogP模式把通信网络抽象为3个参数：L（网络延时），O（通信开销），g（网络带宽）
• 计算过程有若干Superstep组成
• 在每个Superstep中异步地实现局部计算并通过发送/接收L/g报文进行同步

优点

• 可捕捉并行计算机的（同步）通信瓶颈（通过发送或接收L/g个报文）
• 可隐匿拓扑结构，路由算法和网络协议的细节
• 可用于共享变量，报文传递和数据并行处理等方案

缺点

参考文献

https://wenku.baidu.com/view/382879f2561252d381eb6e5f.html?sxts=1542528770069