量子力学——数学

态

　　一个系统的态（state），包含了为了确定它未来的演化，而必须指定的关于这个系统的所有信息。例如，在经典力学中，系统的态是由所有的粒子的位置和动量决定的。而在量子力学中，态即是矢量。

　　我们用符号 |Ψ⟩ 表示态矢量。举一个简单的例子，考虑一个只有两种可能的态的系统，这两种态可以是0/1、上/下、开/关、左/右、死/活等等。这样的一个系统也叫做一个比特。比特的两个态可以用矢量的两个分量来表示。

　　接下来，我们会取一个沿着z-轴自旋的电子，作为在这堂课中将一直用到的物理例子。在经典世界中，电子的自旋要么向上，要么向下。但是，量子世界中的态可以同时是两种态的叠加，比如我们可以将态矢量相加：

　　其中α和β是复数，并且满足|α|²+|β|²=1. 这样的一个态被称为量子比特。也就是说，电子的自旋可以即不向上，也不向下，它是两种可能的态之间的线性叠加。叠加态的可能性是量子力学所有怪异之处的根源。

可观察量

　　我们知道，可观察量（Obsservables）就是那些可以测量的东西。我们也知道，当将矩阵作用于矢量上时，就能产生其他的矢量。在量子力学中，可观察量就是矩阵。

　　对于在一个系统上可以做的每一种测量（比如能量、位置、动量、自旋等等），都存在一个不同的矩阵M。以电子的自旋为例，沿着x-轴、y-轴、z-轴自旋的电子相对应的矩阵分别是：

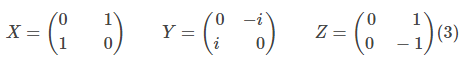
　　通过矩阵乘法，矩阵就可以”作用“在态矢量上。一般来说，当一个矩阵作用在一个矢量上时，会改变矢量的方向。但是，有一些矢量即使经历了矩阵乘法之后，方向也仍保持不变。这些特别的矢量被称为“本征矢量”（eigenvectors）。这意味着：

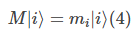
　　其中|i⟩是本征矢量，m_i则是相应的本征值（eigenvalues）。例如，矢量（1）是Z的本征矢量，其本征值为+1和-1，即：

　　在量子力学中，测量就是本征值。

　　也就是说，一个测量的可能结果是与可观察量相关的矩阵M的本征值m_i。但是，如果态不是可观察量M的本征矢量，那么对M的测量结果将是概率性的。

　　测量可以给出任何一个本征值m_i，且每一个都有一定的概率。我们可以以M的本征矢量的基来扩展任意态|Ψ⟩：

　　

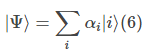
　　其中α_i是复常数。给出本征值m_i的测量概率为|α_i|²（即概率(m_i)=|α_i|²）。且所有概率之和必须为100%。以电子为例，测量到电子自旋向上和向下的概率分别为：

　　且概率之和满足|α|²+|β|²=1。

坍缩

　　在进行测量后，态矢量就会发生坍缩。

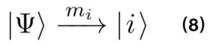
　　也就是说，如果本征值m_i被测量，那么测量后的系统的态是对应的本征矢量|i⟩。如果我们现在重复测量，我们能确定无疑地得到相同的值m_i。但是，如果我们对一个不同的可观察量（对应于一个新矩阵N）进行测量，那么结果会再次是概率性的，除非|i⟩也是N的本征矢量。

　　以电子自旋为例，测量自旋向上或向下的概率分别为|α|²和|β|²。一旦进行了测量，态矢量|Ψ⟩就会坍缩到|↑⟩或|↓⟩，具体坍缩到其中的哪一个态取决于被测量的是哪一个。任何沿着z-轴自旋的后续测量都会得到相同的值。但是，如果我们决定测量一个不同的量，比如沿着x-轴的自旋，那么结果会再次是概率性的。

　　让我们来看一个更加戏剧性的思想实验——薛定谔猫。这只猫处于一个密封的盒子中，盒子中还有一个充满有毒气体氰化氢的玻璃烧瓶和一些放射性物质。倘若盒子里的放射性原子发生了衰变，装有氰化氢的烧瓶就会被打碎，氰化氢挥发导致猫随即死亡；如果放射性物质没有衰变，则不会触发打碎烧瓶的装置，猫能继续存活。一个在盒子之外的观测者在没有打开盒子前，无法得知猫的命运。因此对于观测者而言，猫同时处于生与死的状态。

　　由于放射性的量子力学本质，猫的生或死的态是由量子比特携带的；当我们打开盒子发现猫是死是活的概率由|α|²和|β|²给出；一旦盒子被打开，猫的态就会坍缩成其中的一种。

不确定关系

　　我们刚刚所提到的具有一个重要的含义。大多数矩阵都有不同的本征矢量，这意味着如果态是一个矩阵的本征矢量，它就不太可能是另一个矩阵的本征矢量。因此如果其中一种测量是确定的，那么另一种测量就变得越不确定。

　　这便是海森堡不确定性原理。它说的是，如果我们对粒子的位置知道的越精确，那么对它的动量就知道的越不精确，反之亦然。在经典力学中，我们可以同时精确地知道位置和动量；事实上，我们只有知道这些信息才能预测粒子未来的演化。但是，在量子力学中，如果我们知道一个粒子的位置x，那么就完全无法确定它的动量p，这种关系可以用式子表示：

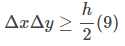
　　其中ħ≈10^-34J⋅s是普朗克常数。我们之所以在日常生活在没有察觉到这些不确定性，是因为ħ太小了。其他的可观察量也存在着类似的不确定性关系。

纠缠

　　当我们结合不同的系统时，就会发现事情变得越来越有趣了。我们可以思考这样一个例子，有两个自旋向上或向下的电子A和B，如果A处于向上的态|↑⟩_A，B处于向下的态|↓⟩_B，那么结合的态为：

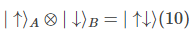
　　左边在数学上称为张量积。右边的第一个箭头代表A的自旋，第二个箭头代表B的自旋。因而总共有四种可能的结合态：|↑↑⟩、|↑↓⟩、|↓↑⟩、|↓↓⟩。态矢量|Ψ⟩可以是这四种态的叠加。例如，如果一个系统的态为：

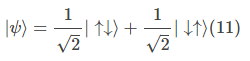
　　由于它不能被分离为单个电子的态的乘积，所以这个系统的态被称为纠缠态。但这并不意味着四种可能的结合态的叠加都是纠缠态。例如另一个积态：

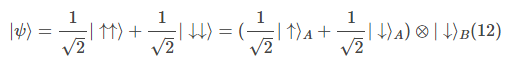
　　积态的主要特征是每个子系统的行为都是相互独立的——如果对B进行一个实验，得到的结果将与A不存在时完全一样。而在纠缠态中，A和B的测量是不独立的。

　　如果一个没有自旋的粒子衰变成两个电子，态（11）就会出现。由于角动量守恒，两个电子的自旋必须是反向对齐的。在经典物理中，该系统则必须处于态|↑↓⟩或|↓↑⟩，但在量子物理中，它可以处于态|↑↓⟩和|↓↑⟩。然后我们将这两个电子分开，比如一个留在地球上，另一个则被送往宇宙的另一端。接着我们测量留在地球上的电子的自旋，测量的结果有50%的可能自旋向上，50%的可能自旋向下。但是，一旦我们测得这个电子的自旋，就能即刻确定在宇宙另一端的电子的自旋。

　　你或许会想，在经典物理中也发生同样的事情。例如你有一对手套，将左右手套分别放入两个不同的盒子中，接着两个盒子被分开的很远。如果你打开其中一个盒子发现里面是左手套，你就立刻能知道另一只无论相距多远的是右手套。这没问题。但是，如果这对手套是量子手套，那么在打开盒子之前，盒子内的量子手套可以是左手套和右手套（以及它们之间的任何东西）。此外，在你观测到右手套之前，左手套还没有成为左手套，只有在观测的那一刻，两只手套才会获得确定的手性。这样的想法令爱因斯坦很沮丧，他将这种现象称为“鬼魅般的超距作用”。