在讲义《线性回归、梯度下降》和《逻辑回归》中我们提到可以用梯度下降或梯度上升的方式求解θ。在本文中将讲解另一种求解θ的方法：牛顿方法（Newton's method）。
牛顿方法（Newton's method）
逻辑回归中利用Sigmoid函数g(z)和梯度上升来最大化ℓ(θ)。现在我们讨论另一个最大化ℓ(θ)的算法----牛顿方法。
牛顿方法是使用迭代的方法寻找使f(θ)=0的θ值，在这里θ是一个真实的值，不是一个参数，只不过θ的真正取值不确定。牛顿方法数学表达式为：
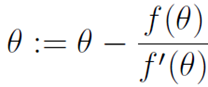
牛顿方法简单的理解方式为：先随机选一个点，然后求出f在该点的切线，即f在该点的导数。该切线等于0的点，即该切线与x轴相交的点为下一次迭代的值。直至逼近f等于0的点。过程如下图：
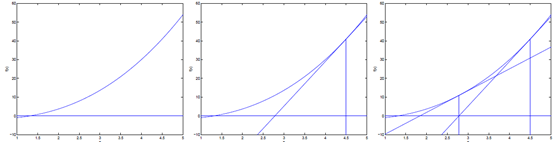
牛顿方法最大化Likelihood
牛顿方法提供了一种寻找f(θ)=0的θ值的方法。怎么用于最大化似然函数ℓ (θ)呢？ℓ的最大值对应点处的一阶导数ℓ'(θ)为零。所以让f(θ) = ℓ'(θ)，最大化ℓ (θ)就可以转化为：用牛顿方法求ℓ'(θ)=0的θ的问题。由牛顿方法的表达式，θ的迭代更新公式为：
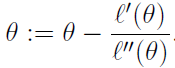
牛顿-拉夫森迭代法（Newton-Raphson method）
逻辑回归中θ是一个向量，所以我们把上面的表达式推广到多维的情况就是牛顿-拉夫森迭代法（Newton-Raphson method），表达式如下：
表达式中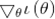
表示的ℓ(θ)对
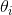的偏导数；H是一个n*n的矩阵，称为Hessian矩阵。Hessian矩阵的表达式为：
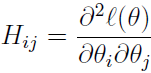
牛顿方法VS梯度下降
如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解：
牛顿方法通常比梯度下降收敛速度快，迭代次数也少。
但因为要计算Hessian矩阵的逆，所以每次迭代计算量比较大。当Hessian矩阵不是很大时牛顿方法要优于梯度下降。