20172322 《程序设计与数据结构》第五周学习总结

20172322 《程序设计与数据结构》第五周学习总结

教材学习内容总结

本章名称 《排序与查找》

• 如果要实现查找到某一对象，就必须能够将一个对象与另一个对象进行比较，故我们需要对所有涉及的元素实现Comparable接口，但是Comparable接口中的compareTo方法可以由我们根据自己的需求进行重写。
  
  这是Java API中的Comparable接口，它存在于java.lang包中。而最终对比的结果大于时返回正整数，等于时返回零，小于时返回负整数。

• 静态方法：使用static修饰符修饰方法，可以使得在调用该方法时不用实例化方法。而静态方法和实例方法的区别主要体现在两个方面，1、在外部调用静态方法时，可以使用"类名.方法名"的方式，也可以使用"对象名.方法名"的方式。而实例方法只有后面这种方式。也就是说，调用静态方法可以无需创建对象。2、静态方法在访问本类的成员时，只允许访问静态成员（即静态成员变量和静态方法），而不允许访问实例成员变量和实例方法；实例方法则无此限制。

• 泛型方法：泛型方法的使用可以在调用的时候指明类型，更加灵活。图例：

  • 定义泛型方法：

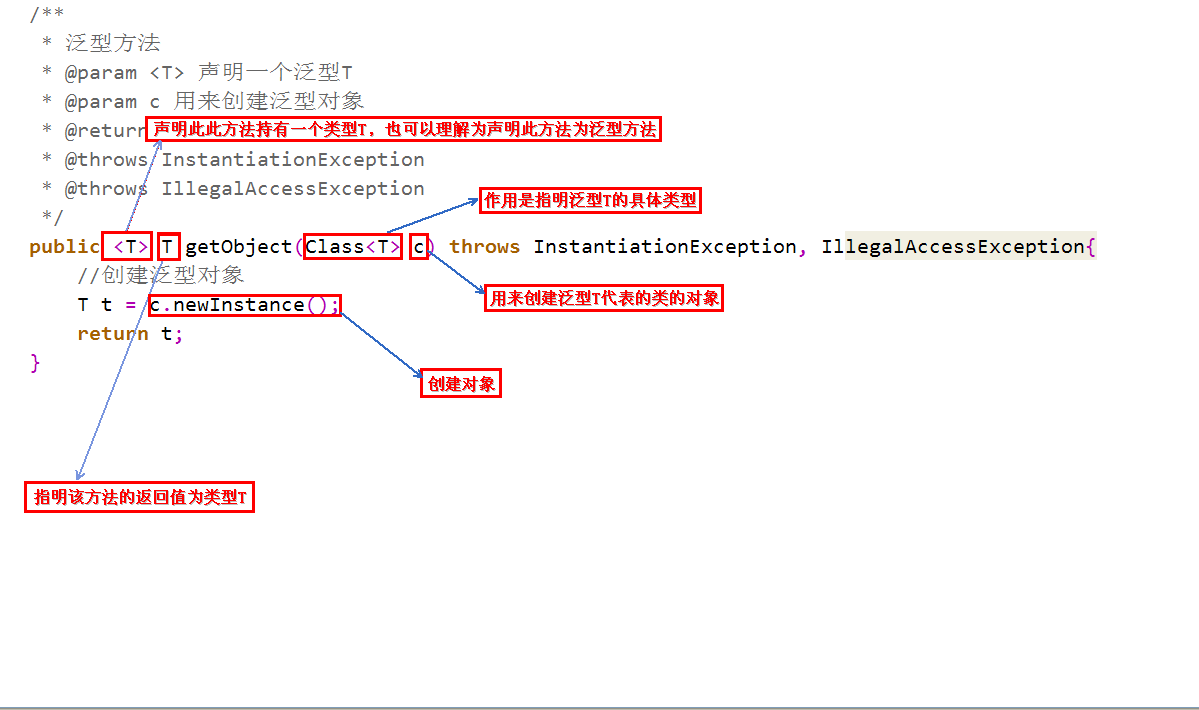
  • 调用泛型方法：

查找

• 线性查找法：一个非常简单的查找方式，从开头或结尾开始查找目标，将每个元素的特征值与查找目标的特征值作比较，最终得出结果。但是在最坏的情况中会遍历整个列表才能查找到该元素。该方法不要求列表是否排序。他的图示如下：

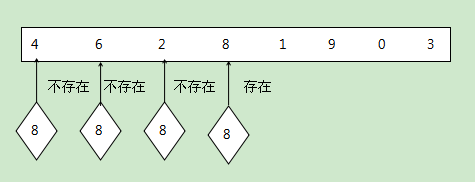
• 二分查找法：从已排序列表的中间开始查找元素，如果没有找到则继续查找，因为列表已排序，故我们就可以仅从列表的一边开始查找下一个元素，因为它必定位于列表的前半部分和后半部分，被我们查找的那一部分被称为可行候选项，图示：

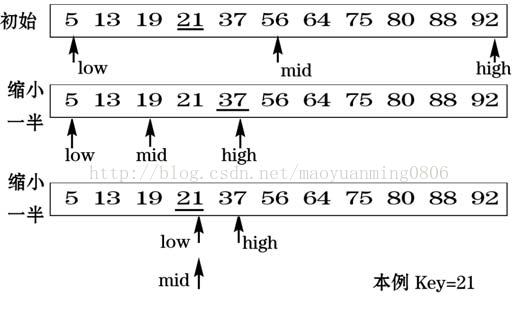
  • 具体的代码实现可以使用递归方法：直接或间接调用自己的算法。例子如下：

  public static <T extends Comparable<T>>  
  	boolean binarySearch(T[] data, int min, int max, T target)
  {  
      boolean found = false;
      int midpoint = (min + max) / 2;  // determine the midpoint
  
      if (data[midpoint].compareTo(target) == 0) {
          found = true;
      } else if (data[midpoint].compareTo(target) > 0)
      {
          if (min <= midpoint - 1) {
              found = binarySearch(data, min, midpoint - 1, target);
          }
      }
      
      else if (midpoint + 1 <= max) {
          found = binarySearch(data, midpoint + 1, max, target);
      }
  
      return found;
  }
  

  在binarySearch方法中直接调用自己，以便实现二分查找。

排序

基于效率的排序算法与查找类似通常分为两类：顺序查找和对数查找，顺序查找通常使用一对嵌套循环对n个元素排序，大约需要n²次比较，而对数查找大约需要nlog₂n次比较。本章中主要涉及五中排序算法，其中顺序排序三种：选择排序、插入排序、冒泡排序，对数排序两种：快速排序、归并排序。

• 选择排序法：首先找出整个列表的最小值与该列表的第一个位置的值进行交换，第二轮扫描除了第一个位置以外的最小值与第二个位置的值进行交换，直至排序完成。图示：

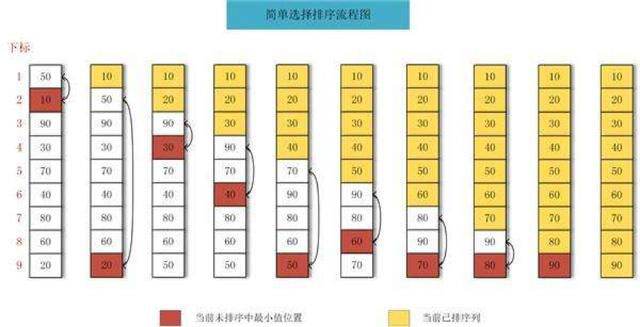
• 插入排序法：先行比较前面两个元素，如有必要就交换顺序，之后扫描后面的元素，将后面的元素插入到前两个元素的应有位置，并且前两个元素也相应的移动。如此往复直至将最后一个元素插入到该有的位置，排序完成。图示：

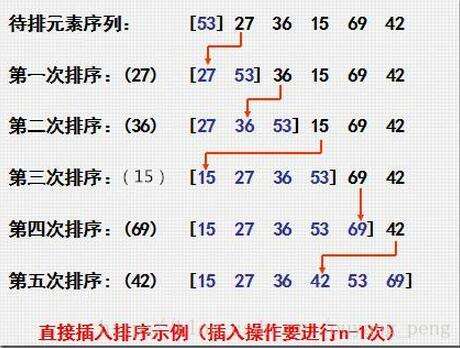
• 冒泡排序法：从第一个元素开始扫描列表并比较相邻的两个元素，按照排序规定选择是否交换位置，直至将最大值“冒泡”至列表的尾端，至此完成一个元素的排序，第二再次扫描列表找到剩下的最大的元素，一路“冒泡”到倒数第二个位置。如此往复，直至排序完成。图示：

• 快速排序法：原理，选择一个关键值作为基准值。比基准值小的都在左边序列（一般是无序的），比基准值大的都在右边（一般是无序的）。一般选择序列的第一个元素。一次循环：从后往前比较，用基准值和最后一个值比较，如果比基准值小的交换位置，如果没有继续比较下一个，直到找到第一个比基准值小的值才交换。找到这个值之后，又从前往后开始比较，如果有比基准值大的，交换位置，如果没有继续比较下一个，直到找到第一个比基准值大的值才交换。直到从前往后的比较索引>从后往前比较的索引，结束第一次循环，此时，对于基准值来说，左右两边就是有序的了。图示：

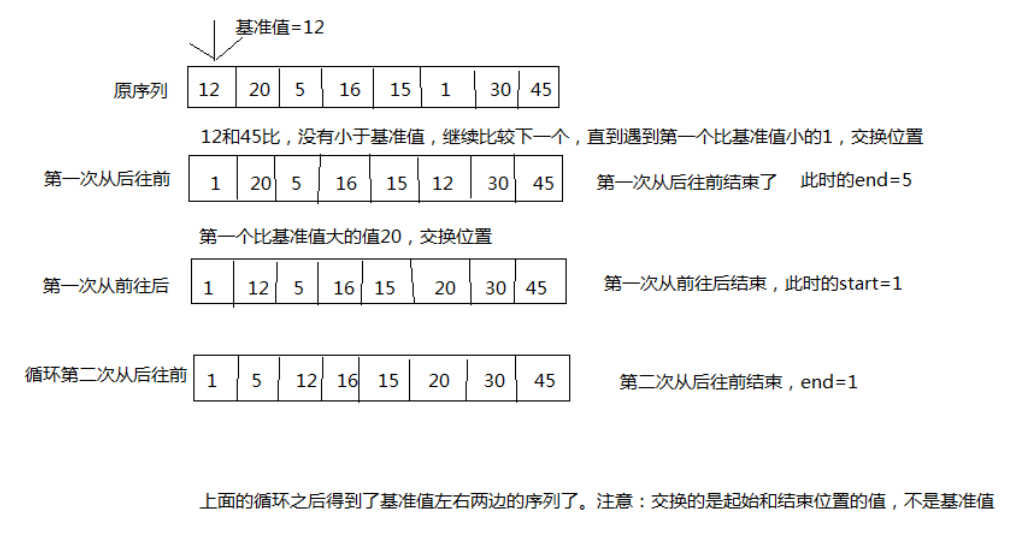
• 归并排序法：其算法是将多个有序数据表合并成一个有序数据表。如果参与合并的只有两个有序表，则成为二路合并。对于一个原始的待排序数列，往往可以通过分割的方法来归结为多路合并排序。图示：

各种排序算法的比较：

教材学习中的问题和解决过程

• 问题一：为什么对数排序通常需要nlog₂n比较呢？

• 问题一解决方案：在网上查阅资料，

  • 对于归并排序法，考虑元素比较次数，两个长度分别为m和n的有序数组，每次比较处理一个元素，因而合并的最多比较次数为(m+n-1)，最少比较次数为min(m,n)。对于两路归并，序列都是两两合并的。不妨假设元素个数为n=2^{h，第一次归并：合并两个长度为1的数组，总共有n/2个合并，比较次数为n/2。第二次归并：合并两个长度为2的数组，最少比较次数是2，最多是3，总共有n/4次，比较次数是(2~3)n/4。第三次归并：合并两个长度为4的数组，最少比较次数是4，最多是7，总共有n/8次合并，比较次数是(4-7)n/8。第k次归并：合并两个长度为2}(k-1)的数组，最少比较次数是2^{(k-1)，最多是2}k-1，总共合并n/(2^{k)次，比较次数是[2^(k-1)~(2^k-1)](n/2^k)=n/2~n(1-1/2}k)。按照这样的思路，可以估算比较次数下界为n/2*h=nlog2(n)/2。上界为n[h-(1/2+1/4+1/8+...+1/2^{h)]=n[h-(1-1/2}h)]=nlog2(n)-n+1。综上所述，归并排序比较次数为nlog2(n)/2~nlog2(n)-n+1。
  • 对于快速排序法，理想情况下，快速排序每次划分都将原始序列划分为两个等长的子序列。所以其比较次数为T(n)=2T(n/2)+n，所以其平均期望时间为nlog(n)。但在最坏情况下，即序列有序情形下，每次划分只能分出一个元素，因而总共需要(n-1)次划分，总的比较次数为(n-1)+(n-2)+...+1=n(n-1)/2，即退化为O(n^2).

• 问题二：对于归并排序法的理解不足，虽然看到书上的例子，但是应该如何去实现，在分解过后的合并排序又是如何实现？

• 问题二解决方案：查阅资料得知，归并排序是将两个或两个以上的有序序列合并成一个新的有序序列。本篇文章介绍的就是归并排序主要是将两个有序数据序列合并成一个新的有序序列。

代码调试中的问题和解决过程

• 问题一：在写PP9.3时的selectionSort方法时，次数输出为零，如图：

问题代码如下：

• 问题一解决：修改frequency变量位置如图：

修改后效果图如下：

代码托管“点这里跳转到码云”

上周考试错题总结

• 错题一：

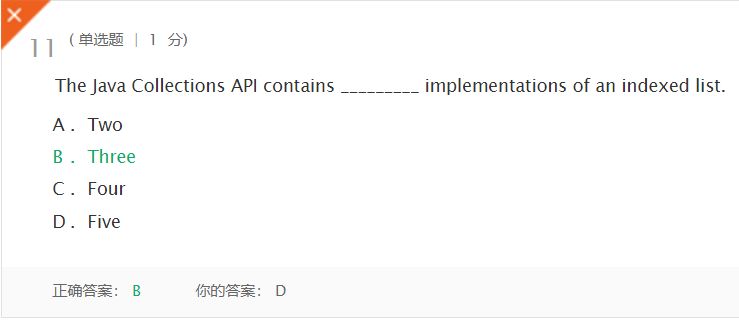
• 解析：书上原话，

Java集合API中含有索引列表的三种实现。

结对及互评

• 博客中值得学习的或问题：
  • 范雯琪同学的博客课本上的学习内容总结部分写得十分详细，值得学习。所以这周我也去学习了一番，在课程学习中图文并茂。
• 代码中值得学习的或问题：
  • commit提交的解释清晰明了，我觉得我应该学习。所以我也学习了部分，细化了commit提交。

点评过的同学博客和代码

• 本周结对学习情况

  • 20172303

  • 结对学习内容

    • 给她讲解了ASL的算法问题。
    • 在她的指导下我的博客有了质的飞跃，从量变到质变。

其他

• 感悟：排序的方法如此之多，每个排序法对需要排序的元素的多少而使用的时间各不相同，在之后的编程中，应该多多想到算法的问题以及复杂度的问题，而不是简单的将作业做出，应该多去想想优化的问题。

课本单词

(本部分用于收集本章节后的生词)

• binary search：二分查找
• bubble sort：冒泡排序
• class method：类方法
• generic method：泛型方法
• insertion sort：插入排序
• linear search：线性查找
• logarithmic algorithm：对数算法
• logarithmic sort：对数排序
• merge sort：归并排序
• partition：分区
• partition element：分区元素
• quick sort：快速排序
• radix sort：基数排序
• searching：查找
• search pool：查找池
• selection sort：选择排序
• sequential sort：顺序排序
• target element：目标元素
• viable candidates：可行候选

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/5000	2/2	8/8	认真学习！积极向上
第二周	812/812	1/3	22/30
第三周	814/1626	1/4	20/50
第四周	1386/3012	2/6	20/70	愉快的国庆节就要结束了...
第五周	1222/3234	1/7	30/100

• 计划学习时间:25小时

• 实际学习时间:30小时

• 改进情况：在博客中图文并茂，commit提交改进。

参考资料

• 《Java软件结构与数据结构》
• Java 中 静态方法与非静态方法的区别
• java实现的快速排序算法
• Java排序之归并排序
• 深入学习排序算法之稳定性、比较次数、交换次数探讨