[ 题解 ] [ 数学 ] 函数 (sequence) (欧拉函数)

题面

馒头卡最近在研究数学，她从八尺深的脑洞里掏出来一个这样的函数，这个函数的定义域为 (N^*)，值域也是 (N^*)，并且这个函数 (f()) 对任意正整数 (n) 满足:

[sum_{d|n}f(d) = n ]

包子卡看了之后表示不服，认为数学不好的馒头卡根本没有研究出这个函数，于是包子卡挑选了几个幸运数字，要求馒头卡给出这些数字的函数值和。馒头卡发现这个答案自己的大脑根本算不出，于是他找到了用计算机的你。

输入
第一行一个整数 (N)，表示包子卡挑选了 (N) 个幸运数字。
接下来一行 (N) 个数字，第 (i) 个数字表示包子卡选择的幸运数字 (A_i)。

输出
一个整数，表示函数值的和，即 (sum_{i=1}^nf(A_i))。

Sample
输入

3
1 2 6

输出

4

样例解释：
(f(1)=1, f(2)=1, f(6)=2)

数据

题解

欧拉函数: (varphi(n)) 为小于 (n) 的正整数中与 (n) 互质的数的数目.

其中欧拉函数有性质：

对于 (forall{m}in N^*)，有

[sum_{d|m} varphi(d) = m ]

证明：

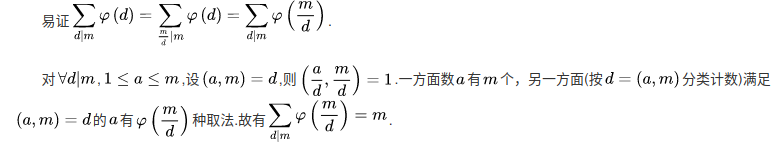
可以看出，原题中的 (f(d) = varphi(d))

求法：

[varphi(m) = mprod_{underset{p为质数}{p|m}}(1 - frac{1}{p}) ]

using i64 = long long;

i64 phi(i64 n)
{
    i64 res = n;
    for (i64 i = 2; i <= sqrt(n); i++)
    {
        if (n % i == 0)
        {
            res = res / i * (i - 1); // res * (1 - 1 / res)
            while (n % i == 0)       // 这样可以使得 i 为质数时才能满足 n % i == 0
                n /= i;
        }
    }

    if (n > 1)
        res = res / n * (n - 1);
    return res;
}

(3): (n = 3 imes 10^7, A_i=7) 这个点答案就是 (n imesvarphi(7))。

(8)(9): (n = 3, n = 5) 这两个点本地算大概两秒就出来了，直接特判输出答案。

Code

#include <iostream>
#include <cmath>

using i64 = long long;

i64 phi(i64 n)
{
    i64 res = n;
    for (i64 i = 2; i <= std::sqrt(n); i++)
    {
        if (n % i == 0)
        {
            res = res / i * (i - 1);
            while (n % i == 0)
                n /= i;
        }
    }

    if (n > 1)
        res = res / n * (n - 1);
    return res;
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cout.tie(0);
    std::cin.tie(0);

    int n;
    std::cin >> n;

    if (n == 3e7)
        std::cout << n * phi(7);
    else if (n == 3)
        std::cout << 525162079891401242;
    else
    {
        i64 ans = 0;
        for (int i = 0; i < n; i++)
        {
            i64 d;
            std::cin >> d;
            ans += phi(d);
        }

        std::cout << ans;
    }
    return 0;
}