[ 算法 ] 细说最短路

[ 算法 ] 细说最短路
前言

最短路问题是信息学竞赛中一个十分重要的问题。在非常多的题目和其他算法、数据结构中都有涉及。最短路算法也是信息学竞赛中的一个难点，对思维能力和代码能力有极大考验和锻炼。目前在网络上没有一个非常完整的最短路详解，各个算法书中也缺乏一些详细的图像和代码来解释，更缺少一些特殊优化及时间复杂度和正确性的详解或证明。本文尝试弥补这些信息的缺失，将会详尽地展示最短路算法的定义、思路、实现、优化和证明等内容。

阅读本文的前置知识：
1. 基础数据结构与算法
2. 搜索算法
3. 图的概念，建立、存储、遍历
4. 动态规划基础思想
定义

(G) 为一张带权有向图，其中 (V) 为其点集合，(E) 为其边集合。

(|V|) 和 (|E|) 分别为点数和边数。

令 (n=|V|) ，(m=|E|) 。

最短路

定义

给定一张有向带权图 (G) ，其中节点以 ([1, n]) 之间的连续整数编号，求以节点 (1) 为起点，到终点 (n) 的最短的路径的长度

简单来说，就是求一张图中以 (1) 为起点，(n) 为终点的最短的一条路径的长度，如下图的最短路即为由 (1) 为起点，(8) 为终点的最短路径：(1 ightarrow2 ightarrow4 ightarrow8) ，其路径长度为 (5+2+1=8) ，小于图中其余的任何路径（如路径(1 ightarrow3 ightarrow8) ，长度为 (1+9=10) ）。

单源最短路

单源最短路问题（Single Source Shortest Path）：给定一张有向带权图 (G) ，求其以 (1) 为起点，到其余每个点的最短路

Bellman-Ford 算法

由理查德·贝尔曼（Richard Bellman）和莱斯特·福特提出的最短路算法

算法思路

要求单源最短路，我们定义 (operatorname{dis}[x]) 表示由 (1) 到 (x) 的最短路的长度。

设有一条边 (u ightarrow v) ，其权值为 (w) ，假设我们已经知道了 (1) 到 (u) 的最短路 (operatorname{dis}[u]) ，那么到达 (v) 且经过 (u) 的最短路 (operatorname{dis}[v]) 就应该是 (operatorname{dis}[u]+w) ，枚举每一条到 (v) 的边 (u ightarrow v) ，那么 (operatorname{dis}[v]=operatorname{min}{operatorname{dis}[u] + w}) 。

如下图，(operatorname{dis}[5]=operatorname{max}(operatorname{dis}[2]+4,operatorname{dis}[3]+3)) 。

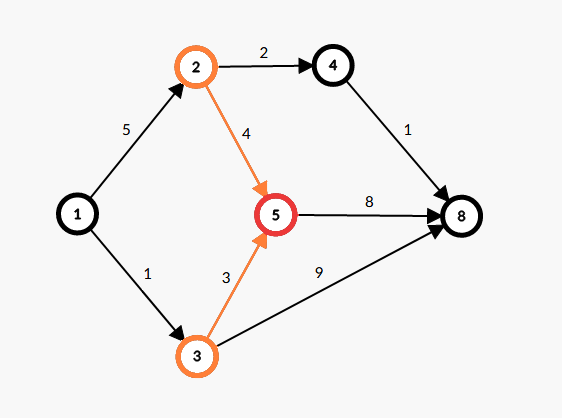
我们称上操作为“松弛操作”。这种操作与动态规划中的许多做法十分相像。

那么，我们只要再知道边界就可以求出整个 (operatorname{dis}) 数组了。不难看出，从 (1) 到 (1) 自身的最短路的长度应为 (0) ，即 (operatorname{dis}[1]=0) 。所以我们只要一直进行松弛操作直到无法再进行松弛即可。

算法流程
1. 枚举所有边 (u ightarrow v) ，进行松弛操作。
2. 重复上操作，直到没有松弛更新的发生。
算法实现
```
struct edge // 一条边上的点 u、点 v、边权 w
{
    int u;
    int v;
    int w;
};
vector<edge> e; // vector 存边方法存图
int dis[MAX];   // 最短路长度

void Bellman_Ford()
{
    // 初始化为无穷大
    for (int i = 0; i < MAX; i++)
        dis[i] = INF;
    dis[1] = 0; // 边界
    while (1)
    {
        bool relaxable = false;
        // edge存边，edge.size() 即为 m
        for (int i = 0; i < edge.size(); i++)
        {
            // 松弛操作
            if (dis[edge[i].v] > dis[edge[i].u] + w)
            {
                dis[edge[i].v] = dis[edge[i].u] + w;
                // 记录是否有进行松弛操作
                flag = true;
            }
        }
        // 若没有进行松弛操作，说明dis已经更新完成，退出
        if (relaxable == false)
            break;
    }
}
```
注：有许多关于 Bellman-Ford 的文章都使用了类似下面的代码——使用双重循环，在第一层中循环 (n) 次。笔者认为其虽简洁，但违背了算法的本意，且拖慢了效率。
```
void Bellman_Ford()
{
    for (int i = 0; i < MAX; i++)
        dis[i] = INF;
    dis[1] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (dis[edge[j].v] > dis[edge[j].u] + w)
                dis[edge[j].v] = dis[edge[j].u] + w;
    }
}
```
算法复杂度

因为在图 (G) 中有 (n) 个点，所以图中的最短路上的点数至多有 (n) 个（否则出现负环，不存在最短路，详见后文）。又因为在每轮遍历所有边时，所有最短路上至少有一个点的 (operatorname{dis}) 被确定了，所以最坏情况下枚举所有边的操作需要被运行 (n) 次。如下图为 (operatorname{dis}) 确定的顺序。（红点为更新过的点）

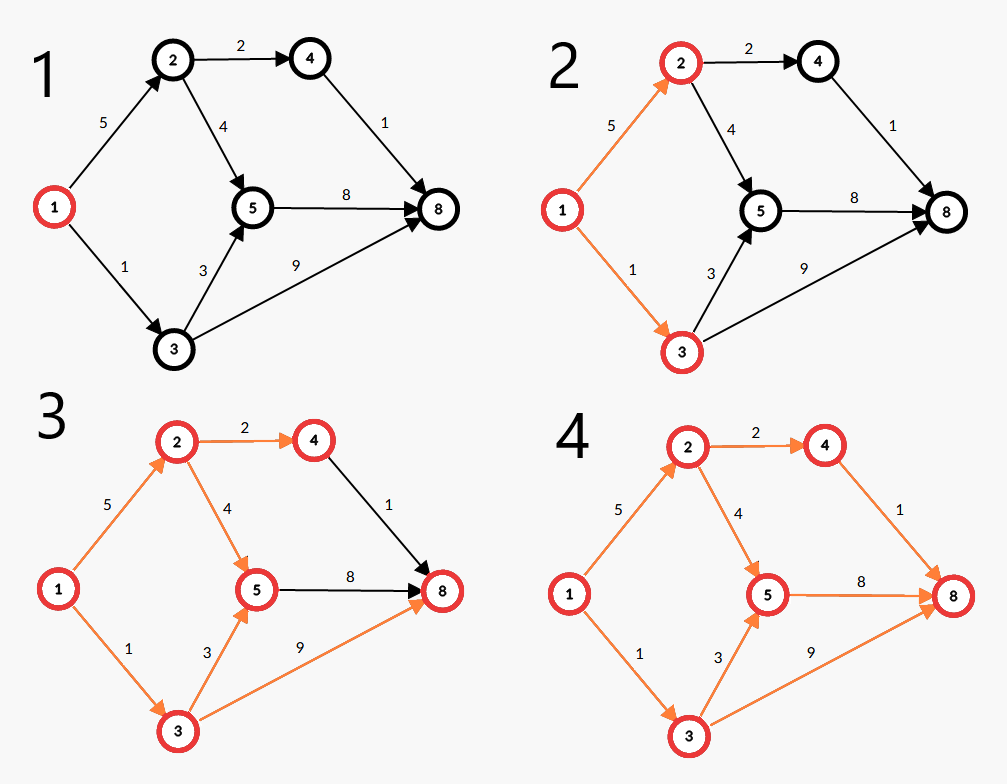
这意味着 Bellman-Ford 的时间复杂度为(点数 imes 边数)： (O(|V||E|)) 即 (O(nm)) ，复杂度较高，十分稳定，一秒大约能处理不足 (1000) 个点。

SPFA 算法

SPFA 算法（Shortest Path Fast Algorithm 最短路快速算法）：Bellman_Ford 的优化

算法思路

在前文 Bellman-Ford 算法中，使用了枚举边进行松弛操作来求出 (operatorname{dis}) 数组。而在分析其算法时间复杂度时，可以看出一个 Bellman-Ford 有很多重复的计算。在确定了靠近起点的点的 (operatorname{dis}) 值后，之后的枚举重复计算了已经确定的 (operatorname{dis}) 值。实际上我们无需关注之前的 (operatorname{dis}) 值，只要知道连向当前点的节点的 (operatorname{dis}) 值就足够了。

就此问题，我们可以对其进行优化。我们发现，(operatorname{dis}) 的确定顺序和 BFS 搜索的顺序相同，我们可以使用 BFS 优化 Bellman-Ford 算法。

只需从起点开始，BFS 搜索，搜索到一个点后松弛更新它连接到的所有点，出 (operatorname{dis}) 数组的值。

如下图，即为 SPFA 算法的更新方法。（红点：在队列中的点；蓝点：被更新的点；灰点：确定了(operatorname{dis}) 值的点）

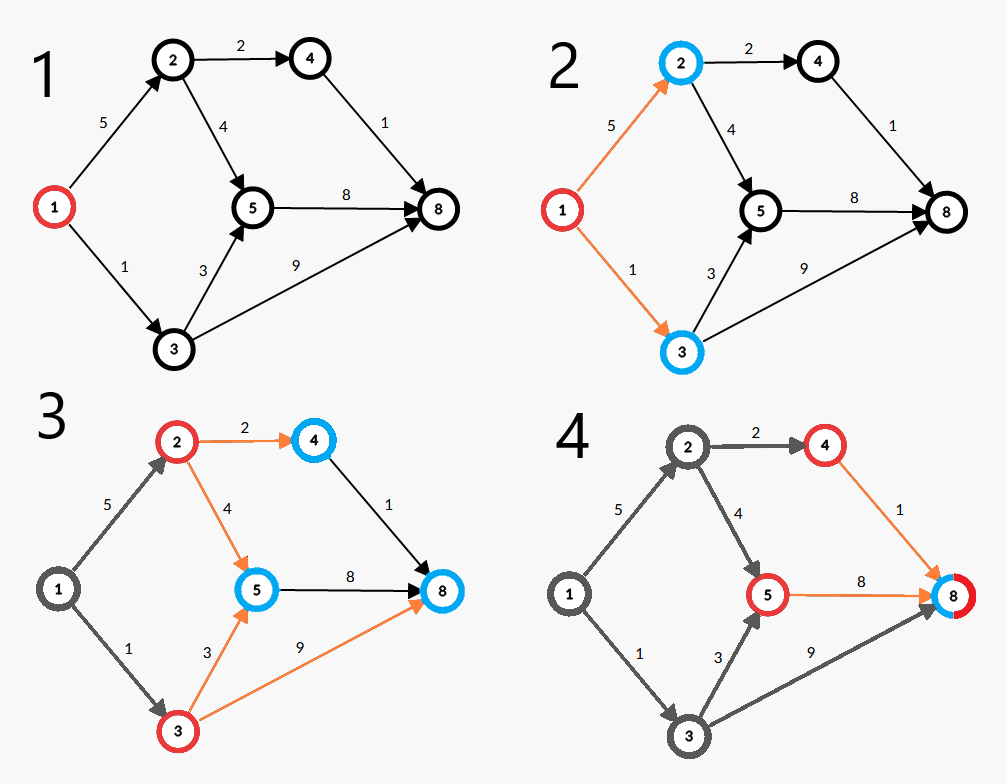
算法流程
1. 新建一个队列 (q) 用于进行 BFS 搜索，开始搜索前队列中只有起始点 (1)，建立 (operatorname{inque}) 哈希表，表示某个点是否在队列中。
2. 进行 BFS 搜索，每次取出队列头 (u)，枚举所有从 (u) 出发的边 (u ightarrow v) ，对 (v) 进行松弛操作（若 (operatorname{dis}[v] > operatorname{dis}[u] + w) 则 (operatorname{dis}[v] = operatorname{dis}[u] + w)）同时若 (v) 不在队列中，则使 (v) 入队。
3. 重复上述操作直至队列为空，搜索结束。
算法实现
```
struct node // 邻接表 u 的对应点 v 和边权 w
{
    int v;
    int w;
};
vector<node> g[MAX]; // vector 邻接表存图
bool inque[MAX];     // 队列状态哈希表
int dis[MAX];        // 最短路长度

void SPFA()
{
    // 初始化为无穷大
    for (int i = 0; i < MAX; i++)
        dis[i] = INF;
    dis[1] = 0;        // 边界
    queue<int> q;      // 创建队列
    q.push(1);         // 初始化队列
    inque[1] = true;   // 记录 inque 状态
    while (!q.empty()) // 执行 BFS 直到队列为空
    {
        int u = q.front(); // 取出队头
        q.pop();           // 弹出队头
        inque[u] = false;  // 去除 inque 记录
        // 枚举被松弛的点 v
        for (int i = 0; i < g[u].size(); i++)
        {
            int v = g[u][i].v;
            int w = g[u][i].w;
            // 松弛操作
            if (dis[u] + w < dis[v])
            {
                dis[v] = dis[u] + w;
                // 入队
                if (!inque[v])
                {
                    inque[v] = true;
                    q.push(v);
                }
            }
        }
    }
}
```
算法复杂度

SPFA 算法的主要核心为 BFS 搜索，遍历所有的点，但也会重复更新一定的点，时间复杂度大约为 (O(k|E|)) （即(O(km))）其中 (k) 为常数，(k) 在稀疏图中约为 (2) 但在稠密图中可能会严重退化。在特殊数据中最坏退化到 (O(|V||E|)) ，与 Bellman-Ford 相同，极其不稳定，最佳每秒能处理大约 (50,000,000) 个点，最差仅能处理不足 (1000) 个点。

算法正确性

由于是按照 BFS 搜索顺序在有向图中搜索，对于所有点 (v) ，其对应的边 (u ightarrow v) 中的所有 (u) 在搜索结束前都一定被访问过，所以 (operatorname{dis}[v]) 一定被更新了足够多次，使得满足松弛操作中的式子 (operatorname{dis}[v]=operatorname{min}{operatorname{dis}[u] + w}) 。

算法优化

由于 SPFA 算法的效率波动大，因此产生了许多种优化。

整理自：SPFA算法的玄学方法

基础优化

SLF (Small Label First) 优化

将朴素 SPFA 的队列 queue 替换为双端队列 deque 。在每次插入对位元素 (v) 时，将其与队首进行比较，若 dis[dq.front()] > dis[v] 将 (v) 由队首插入，否则从队尾插入。
```
deque<int> dq;
dq.push_back(1);
inque[1] = true;
while (!dq.empty())
{
    int u = dq.front();
    dq.pop_front();
    inque[u] = false;
    for (int i = 0; i < g[u].size(); i++)
    {
        int v = g[u][i].v;
        int w = g[u][i].w;
        if (dis[u] + w < dis[v])
        {
            dis[v] = dis[u] + w;
            if (!inque[v])
            {
                inque[v] = true;
                // 若 dis[dq.front()] > dis[v] 将 v 由队首插入，否则从队尾插入
                if (dq.empty() || dis[v] > dis[dq.front()])
                    dq.push_back(v);
                else
                    dq.push_front(v);
            }
        }
    }
}
```
SLF 通过将最小的结果放在队列前端，可以更早地更新出节点的最优解，又根据已有的最优解，更快地更新出所有最优解。

LLL (Large Label Last）优化

同样将队列换为双端队列。维护队列中元素 (operatorname{dis}) 的平均值，设为 (k) ，若 dis[v] > k ，从队尾插入，然后继续寻找，直到有 dis[x] <= k 。

LLL 在遇到特殊数据时可能被卡成指数级。

升级优化

容错 SLF

设定容错值 (val) ，当满足 dis[v] > dis[dq.front()] + val 时从队尾插入，否则从队首插入。

mcfx 优化

mcfx 优化定义区间 ([l,r]) ，当入队节点的入队次数属于这个区间的时候，从队首插入，否则从队尾插入。

Swap-SLF

若队列改变且 dis[dq.front()] > dis[dq.back()] ，交换队首队尾。
```
if (dis[dq.front()] > dis[dq.back()])
{
    int tmp = dq.front();
    dq.pop_front();
    dq.push_front(dq.back());
    dq.pop_back();
    dq.push_back(tmp);
}
```
优化的兼容性

LLL 和 SLF ，

容错 SLF 和 mcfx ，

可以同时使用。

以上多种优化能有一定的常数级优化效果，但在特殊构造的数据下还是会严重退化。

SLF 优化：每次将入队结点距离和队首比较，如果更大则插入至队尾。

Hack：使用链套菊花的方法，在链上用几个并列在一起的小边权边就能欺骗算法多次进入菊花。

LLL 优化：每次将入队结点距离和队内距离平均值比较，如果更大则插入至队尾。

Hack：向 1 连接一条权值巨大的边，这样 LLL 就失效了。

SLF 带容错：每次将入队结点距离和队首比较，如果比队首大超过一定值则插入至队尾。

Hack：卡法是卡 SLF 的做法，并开大边权，总和最好超过 (10^{12})。

mcfx 优化：在第 ([L,R])次访问一个结点时，将其放入队首，否则放入队尾。

Hack：网格图表现优秀，但是菊花图表现很差。

SLF + swap：每当队列改变时，如果队首距离大于队尾，则交换首尾。

Hack: 与卡 SLF 类似，外挂诱导节点即可。

——知乎用户 in 如何看待 SPFA 算法已死这种说法？

其他优化

改变数据结构

使用 priority_queue 代替 queue 或使用 zkw 线段树

随机化
1. 边序随机 将边随机打乱后进行 SPFA。
2. 队列随机 每个节点入队时，以 (frac{1}{2}) 的概率从队首入队，(frac{1}{2}) 的概率从队尾入队。
3. 队列随机优化版 每 (C) 次入队后，将队列元素随机打乱。
随机化可以加快数学期望上的时间复杂度，但对于渐进上界 (O) 记号来讲没有改变，这种做法只能在竞赛中让 SPFA 算法勉强躲过构造的数据。

Dijkstra 算法

迪杰斯特拉算法（Dijkstra）由荷兰计算机科学家狄克斯特拉于1959 年提出。Dijkstra 算法只在非负权有向图中适用（SPFA 可以在所有有向图中使用）。

算法思路

Dijkstra 算法的基本思路是贪心。Dijkstra 同样引入 (operatorname{dis}) 数组，表示点到原点的最短路的长度。同时，Dijkstra 维护一个确定了 (operatorname{dis}) 值的点的集合 (C) 。

在 Bellman-Ford / SPFA 中，用遍历边的方式，松弛更新每个点的 (operatorname{dis}) 值。而在 Dijkstra 中，用贪心的方法可以尽快确定 (operatorname{dis}) 值，减少无用操作。贪心的方法十分简单，每次寻找不在集合 (C) 中 (operatorname{dis}) 值最小的点 (u) ，枚举所有边 (u ightarrow v) ，松弛更新 (operatorname{dis}[v]) 。

如下图所示，即为 Dijkstra 算法的模拟。（红点：点 (u) ，橙边：边 (u ightarrow v) ，蓝点：点 (v) ，灰点：在集合 (C) 中的点）

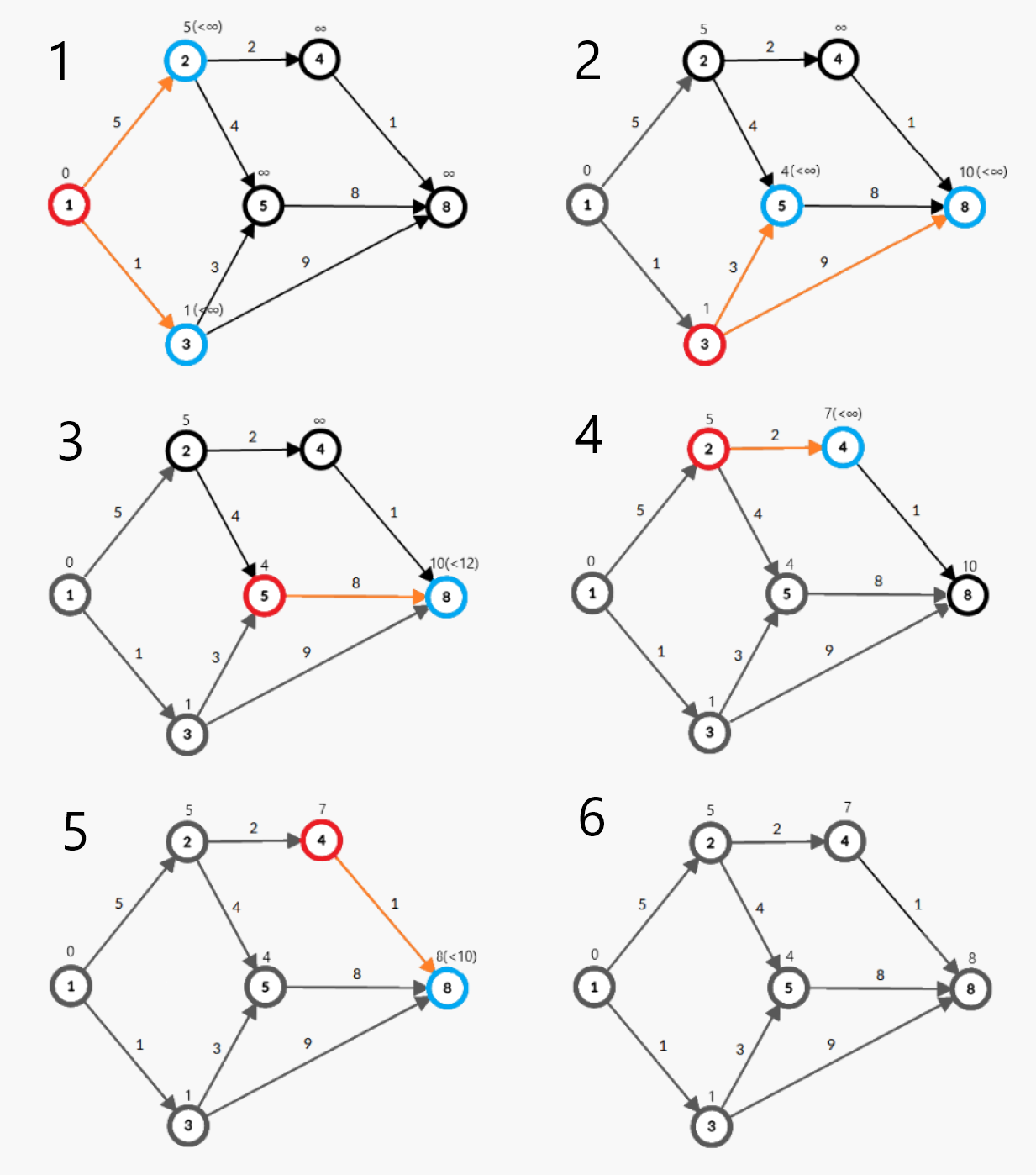
算法流程
1. 初始化 (operatorname{dis}[1]=0) ，其余 (operatorname{dis}) 为 (infin) 。
2. 找到不在确定 (operatorname{dis}) 集合 (C) 中 (operatorname{dis}) 值最小的点 (u) 。
3. 枚举所有 (u) 的出边 (u ightarrow v) 。
4. 松弛更新点 (v) ，若 dis[v] > dis[u] + w ，则使 dis[v] = dis[u] + w 。
5. 重复 ([2,3,4]) 步，直到 (C=V) （(V) 为图 (G) 的点集）。
算法实现
```
struct node // 邻接表 u 的对应点 v 和边权 w
{
    int v;
    int w;
};
vector<node> g[MAX]; // vector 邻接表存图
bool vis[MAX];       // 已确定 dis 值的点集 C, vis[x] 为 true 表示在集合中
int dis[MAX];        // 最短路长度

void Dijkstra()
{
    // 初始化为无穷大
    for (int i = 0; i < MAX; i++)
        dis[i] = INF;
    dis[1] = 0;
    // 由于每次确定一个点的 dis 值，所以需要循环 n 次才使得 C = V
    // 从算法思路中的图可以看出
    for (int i = 0; i < n; i++)
    {
        int u = 0;
        // 枚举所有点，寻找不在集合 C 中 dis 值最小的点
        for (int j = 1; j <= n; j++)
            if (!vis[j] && (u == 0 || dis[j] < dis[u]))
                u = j;
        // 将找到的点 u 加入集合 C
        vis[u] = true;
        // 枚举 u 的出边 u -> v ，进行松弛更新
        for (int j = 0; j < g[u].size(); j++)
        {
            int v = g[u][j].v;
            int w = g[u][j].w;
            if (!vis[v] && dis[u] + w < dis[v])
                dis[v] = dis[u] + w;
        }
    }
}
```
算法复杂度

由上方代码容易看出，我们需要循环 (n) 次，在循环内每次枚举所有的点，再枚举所有的出边。

循环 (n) 次，每次遍历所有的点需要 (n^2) 次，每次枚举出边共需要 (m) 次。所以 Dijkstra 算法的时间复杂度为 (|V|^2+|E|) ，又因为 (|E|) 的值最大为所有点均相互连边的边数，即为 (C^2_{|V|}=frac{|V| imes (|V|-1)}{2}<|V|^2) 所以可以将 (|E|) 视为常数。

综上，Dijkstra 算法的时间复杂度应为 (O(|V|^2)) (即 (O(n^2)))。

堆优化

朴素 Dijkstra 的时间复杂度为 (O(n^2)) ，在实际应用中还有很大的常数，运行效率甚至低于 Bellman_Ford（详见下文 5.1, 5.3 算法实际效率测试）。但是 Dijkstra 算法 + 堆优化的效率可以接近 SPFA ，且非常稳定，没有退化风险。是求非负权有向图上单源最短路的主流做法。

优化思路

由 4.3.4 Dijkstra算法复杂度中的分析，可以发现，朴素 Dijkstra 算法的效率瓶颈在于寻找图中 (operatorname{dis}) 值最小的点。其实我们没有必要每次都遍历所有的点来寻找 (operatorname{dis}) 值最小的。我们可以使用堆，每次只要取出堆顶的点即可。

因为所有确定的点（在集合 (C) 中的点）不会被作为前文 Dijkstra 中的点 (u) 即前文图中的红点使用，而其余没有变为蓝点过，即没有被进行松弛更新的点的 (operatorname{dis}) 值都为 (infin) 。所以只有被松弛更新过，且不在集合 (C) 中的点可能是 (operatorname{dis}) 值最小的点 (u) 。

所以我们可以使用类似 BFS 的方法，在每次进行松弛更新时把点放入堆中。

优化实现

在 C++ 中，我们可以使用 STL 中的 priority_queue 代替堆，相较于手写堆方便很多。

值得注意的是，用堆记录最小 (operatorname{dis}) 值的点时，我们要将点按 (operatorname{dis}) 值排序，导致点自身的序号顺序被打乱，需要专门记录，且需要自己在结构体 / 类中重载比较符号。当然，也可以使用 STL 中的 pair 。
```
struct node
{
    int v;
    int w;
};
struct data
{
    int dis; // 用于在优先队列中找出所有点中 dis 值最小的点
    int num; // 用于记录这个点的编号
    // 重载符号 >
    bool operator>(const data x) const
    {
        if (this->dis != x.dis)
            return this->dis > x.dis;
        return this->num > x.num;
    }
};
vector<node> g[MAX];
bool vis[MAX];
int dis[MAX];

void Dijkstra()
{
    // 初始化为无限大
    for (int i = 0; i < MAX; i++)
        dis[i] = INF;
    dis[1] = 0;
    // 声明优先队列，相当于小根堆
    priority_queue<data, vector<data>, greater<data>> pq;
    pq.push((data){0, 1}); // 初始化优先队列，插入起点
    while (!pq.empty())
    {
        // 取出堆顶
        int u = pq.top().num;
        pq.pop();
        // u 不可以在集合 C 中
        if (vis[u])
            continue;
        vis[u] = true; // 将 u 加入集合 C
        for (int i = 0; i < g[u].size(); i++)
        {
            int v = g[u][i].v;
            int w = g[u][i].w;
            // 松弛操作
            if (!vis[v] && dis[u] + w < dis[v])
            {
                dis[v] = dis[u] + w;
                // 将有可能是所有点中 dis 值最小的点加入堆中
                pq.push((data){dis[v], v});
            }
        }
    }
}
```
pair 写法：
```
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push(make_pair(0, s));
int u = pq.top().second;
pq.push(make_pair(dis[v], v));
```
算法实际效率测试

洛谷 P4779 ，C++11 O2 测试结果

共 6 个数据点

Bellman-Ford

Bellman-Ford: 6.07s

#1 #2 #3 #4 #5 #6

TLE TLE TLE TLE AC TLE

SPFA

朴素 SPFA: 5.00s

#1 #2 #3 #4 #5 #6

TLE TLE TLE AC AC TLE

SPFA + SLF: 4.76s

#1 #2 #3 #4 #5 #6

AC TLE TLE AC AC TLE

SPFA + SLF + LLL: 6.10s

注：由于此题卡 SPFA ，LLL 优化被卡成指数级别了

#1 #2 #3 #4 #5 #6

TLE TLE TLE TLE AC TLE

SPFA + 容错 SLF + mcfx: 515ms

#1 #2 #3 #4 #5 #6

AC AC AC AC AC AC

SPFA + SLF + Swap-SLF: 3.92s

#1 #2 #3 #4 #5 #6

AC TLE TLE AC AC TLE

SPFA + 优先队列: 2.79s

#1 #2 #3 #4 #5 #6

TLE AC AC AC AC TLE

SPFA + 队列随机: 4.95s

#1 #2 #3 #4 #5 #6

TLE TLE TLE AC AC TLE

Dijkstra

朴素 Dijkstra: 7.20s

#1 #2 #3 #4 #5 #6

TLE TLE TLE TLE TLE TLE

Dijkstra + 堆优化: 660ms

#1 #2 #3 #4 #5 #6

AC AC AC AC AC AC

参考资料
1. 李煜东《算法竞赛进阶指南》
2. 刘汝佳《算法竞赛入门经典》
3. 《算法导论》
4. SPFA算法的玄学方法
5. 知乎：如何看待 SPFA 算法已死这种说法？
6. struct Edge SPFA算法
7. Dijkstra、Bellman_Ford、SPFA、Floyd算法复杂度比较
8. Ateisti: spfa + slf优化
9. 姜碧野《迭代求解的利器--spfa算法的优化及其应用》
10. yasolx SPFA的SLF与LLL优化
11. little_sun dijkstra 详解
12. 绝顶我为峰学图论，你真的了解最短路吗？
相关阅读:
于丹的婚姻观
 相貌与成功的关系—俞敏洪6月2号在同济大学的演讲
 NetBeans IDE 6.9.1 发布
 NetBeans IDE 6.9.1 发布
 NetBeans 时事通讯（刊号 # 112 Aug 05, 2010）
VS Feature Pack学习之使用CMFCMenuBar自定义菜单栏
 使用 Apache Wink、Eclipse 和 Maven 开发 RESTful Web 服务
 Have to run sudo dhclient eth0 automatically every boot
java regex
HTTPCLIENT 解决乱码方案 linfeng_0212的日志网易博客
原文地址：https://www.cnblogs.com/zhangtianli/p/13403646.html

[ 算法 ] 细说最短路

前言

定义

最短路

定义

单源最短路

Bellman-Ford 算法

算法思路

算法流程

算法实现

算法复杂度

SPFA 算法

算法思路

算法流程

算法实现

算法复杂度

算法正确性

算法优化

基础优化

SLF (Small Label First) 优化

LLL (Large Label Last）优化

升级优化

容错 SLF

mcfx 优化

Swap-SLF

优化的兼容性

其他优化

改变数据结构

随机化

Dijkstra 算法

算法思路

算法流程

算法实现

算法复杂度

堆优化

优化思路

优化实现

算法实际效率测试

Bellman-Ford

SPFA

Dijkstra

参考资料