第二章 线性表
参考文献:[数据结构(C语言版)].严蔚敏
本篇章仅为个人学习数据结构的笔记,不做任何用途。
2.1 线性结构的特点
(1). 存在唯一的一个被称为"第一个"的数据元素
(2). 存在唯一的一个被称为"最后一个"的数据元素
(3). 除第一个之外,集合中的每个数据元素均有唯一的前驱
(4). 除最后一个之外,集合中的每个数据元素均有唯一的后继
2.2 线性表的类型定义
线性表(linear_list) 是最简单最常用的一种数据结构。一个线性表是n个数据元素的有限序列。
例如,26个英文字母的字母表:
上述是一个线性表,数据元素是单个字母字符。
例如,一个家庭中各个家庭成员的年龄,可用线性表的形式给出:
上述线性表中的数据元素是整数。
复杂的线性表情况如下:
- 一个数据元素有若干个 数据项(item) 组成。
- 如上情况,数据元素称为 记录(record)。
- 含有大量记录的线性表称为 文件(file)。
例如,一个学生的学生健康情况登记表。表中每个学生的情况为一个记录。
它由姓名,学号,性别,年龄,班级等5个数据项组成。
| 姓名 | 学号 | 性别 | 年龄 | 班级 |
|---|---|---|---|---|
| 张盛东 | 790302 | 男 | 28 | 计科062 |
| 卢晔 | 790303 | 女 | 26 | 计科061 |
因此,线性表的抽象描述如下:
当i=1,2,...,n-1时,ai有且仅有一个直接后继。
当i=2,3,...,n时,ai有且仅有一个直接前驱。
线性表中元素的个数n(n>=0)定义为线性表的长度,n=0为空表。
非空表中的每个数据元素都有一个确定的位置。如a1是第一个数据元素,如an是最后一个数据元素,ai是第i个元素,i为数据元素ai在线性表的位序。
抽象数据类型的结构:
ADT 抽象数据类型名{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
} ADT 抽象数据类型名
抽象数据类型线性表的定义:
ADT List{
数据对象:D ={a(i)|a(i) 属于ElemSet, i=1,2,...,n,n>=0}
数据关系:R ={<a(i-1),a(i)>|<a(i-1),a(i) 属于D,i=2,...,n}
基本操作:
InitList(&L)
操作结果:构造一个空的线性表L。
DestoryList(&L)
初始条件:线性表L已存在。
操作结果:销毁线性表L。
ClearList(&L)
初始条件:线性表L已存在。
操作结果:将L重置为空表。
ListEmpty(L)
初始条件:线性表L已存在。
操作结果:判断L是否为空表,是的话返回True,不是返回False。
ListLength(L)
初始条件:线性表L已存在。
操作结果:返回L中数据元素的个数。
GetElem(L,i,&e)
初始条件:线性表L已存在,1<=i<=ListLength(L)
操作结果:用e返回L中第i个数据元素的值。
LocateElem(L,e,compare())
初始条件:线性表L存在,compare()是数据元素判定函数。
操作结果:返回L中第一个与e满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回值为0。(通俗来讲,就是返回数据元素的位置)
PriorElem(L,cur_e,&pre_e)
初始条件:线性表L已存在。
操作结果:若cur_e是L的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e不存在。(通俗来讲,返回数据元素的前驱)
NextElem(L,cur_e,&next_e)
初始条件:线性表L已存在。
操作结果:若cur_e是L的数据元素,且不是最后一个,则用next_e返回它的后继,否则操作失败,next_e不存在。(通俗来讲,返回数据元素的后继)
ListInert(&L,i,e)
初始条件:线性表L已存在,1<=i<=ListLength(L)+1。
操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1。
ListDelete(&L,i,&e)
初始条件:线性表L已存在,1<=i<=ListLength(L)。
操作结果:删除L中第i个数据元素,并用e返回其值,L的长度减1。
ListTraverse(L,visit())
初始条件:线性表L已存在。
操作结果:依次对L的每个数据元素调用visit()。一旦visit()失败,则操作失败。
(通俗来讲,对每一个数据元素进行遍历)
} ADT List
2.3 线性表的顺序表示和实现
线性表的顺序表示 指的是用一组地址连续的存储单元依次存储线性表的数据元素。
假设线性表的每个元素需要用l个存储单元,并以所占的第一个单元的存储地址作为数据元素的存储位置。则第i+1个数据元素的存储位置LOC(a1+1)和第i个数据元素的存储位置LOC(ai)满足如下关系:
上述的这种表述称为线性表的顺序结构。亦或者称为顺序映像(sequential mapping)。其特点为:
相邻的两个数据元素ai和a1+1。其存储的"物理位置"也相邻。示意图如下:

由于确定了存储线性表的起始位置,每一个数据元素的存储位置都和线性表的起始位置相差一个和数据元素在线性表中的位序成正比的常数,线性表中任一数据元素都可随机存取,所以线性表的顺序结构是一种随机存取的存储结构。
C语言中可用动态分配的一维数组,来描述线性表的顺序存储结构,其中数组指针elem指示线性表的基地址,length代表线性表的当前长度,如下:
// - - - - - 线性表的动态分配顺序存储结构 - - - - -
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct {
ELemType * elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemTpye)为单位)
}SqList;
如下算法用于构造一个空的线性表。初始化操作是为顺序表分配一个预定义大小的数组空间,并将线性表的当前长度设为"0"。listsize为当前分配的存储空间大小。
Status InitList_Sq(SqList &L){
//构造一个空的线性表L。
L.elem = (ELemType *)malloc(LIST_INIT_SIZE * sizeof(ELemType));
if(! L.elem) exit(OVERFLOW); //存储分配失败
L.length = 0; //空表长度为0
L.listsize = LIST_INIT_SIZE; //初始化存储容量
return OK;
}// InitList_Sq
线性表的顺序存储的插入操作:
例如:在线性表的第i-1个数据元素和第i个数据元素之间插入一个新的数据元素,会使得长度为n的线性表。
在线性表中的顺序存储结构中,由于逻辑上相邻的数据元素在物理位置上也是相邻的。因此,插入数据元素,存储位置有如下的变化。
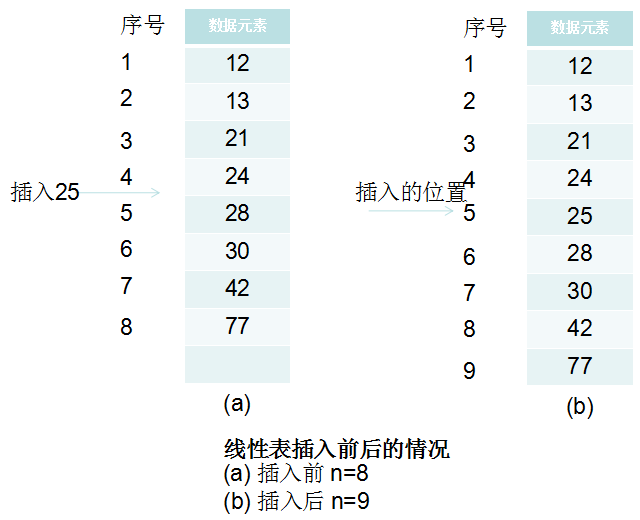
顺序线性表的插入算法:
Status ListInsert_Sq(SqList &L,int i,ElemType e){
//在顺序线性表中L中第i个位置之前插入新的元素e。
//i的合法值为1<=i<=ListLength_Sq(L)+1
if(i < 1 || i >L.length+1) return ERROR; //i值不合法
if(L.length >L.listsize){
newbase = (ElemType *)realloc(L.elem,(L.listsize+LISTINCREMENT) * sizeof(ElemTpye));
if(! newbase)exit(OVERFLOW); //存储分配失败
L.elem = newbase; //新基址
L.listsize += LISTINCREMENT; //增加存储容量
}
q = &(L.elem[i-1]); //q为插入位置
for (p = &(L.elem[L.length-1]);p >= q; --p)
*(p+1) =*p; //插入位置及之后的元素后移
* q =e; //插入e
++L.length; //线性表长度+1
return OK;
}// ListInsert_Sq
线性表的顺序存储的删除操作:
例如:在线性表中删除一个数据元素,会使得长度为n的线性表。
删除数据元素,存储位置有如下变化。
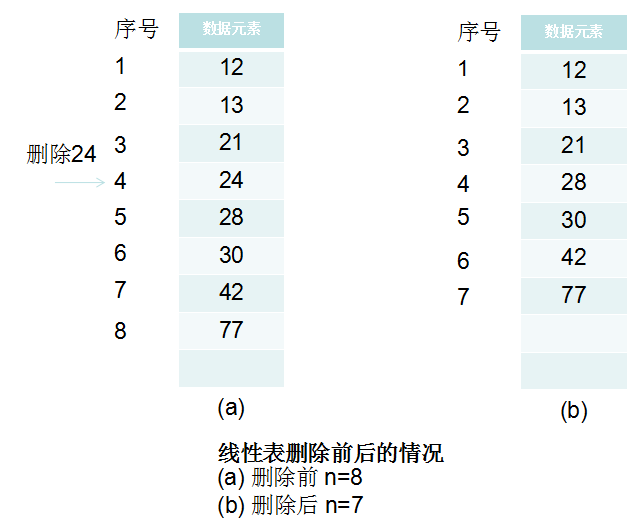
顺序线性表的删除算法:
Status ListDelete_Sq(SqList &L,int i,ElemType &e){
//在顺序线性表中L中删除第i个元素,并用e返回其值。
//i的合法值为1<=i<=ListLength_Sq(L)
if(i < 1 || i >L.length+1) return ERROR; //i值不合法
p = &(L.elem[i-1]); //q为删除元素的位置
e = *p; //被删除元素的值赋予e
q = L.elem+L.length-1; //表尾元素的位置
for(++p;p<=q,++p) *(p-1) = *p; //被删除元素之后的位置左移
--L.length; //线性表长度-1
return OK;
}// ListDelete_Sq
线性表的顺序存储的查找操作:
顺序线性表的查找算法:
int LocateElem_Sq(SqList L,ElemType e,Status (*compare)(ElemType,ElemType)){
//在顺序线性表中L中查找第一个与e满足compare()的元素的位序。
//若找到,则返回其在L中的位序,否则返回0。
i = 1 //i的初值为第一个元素的位序。
p = L.elem; //p的初值为第一个元素的存储位置。
while(i<=L.length && !(*compare)(* p++,e)) ++i;
if(i<=L.length) return i;
else return 0;
}// LocateElem_Sq
线性表的顺序存储的合并操作:
void MergeList_Sq(SqList La,Sqlist Lb,SqList &Lc) {
// 已知顺序线性表La和Lb的元素按值非递减排列
//归并La和Lb得到的新的顺序线性表Lc,Lc的元素也按值非递减排列
pa =La.elem; pb=Lb.elem;
Lc.listsize =Lc.length = La.length+Lb.length;
pc = Lc.elem =(ElemTpye *)malloc(Lc.listsize *sizeof(ElemTpye));
if(!Lc.elem)exit(OVERFLOW); //存储分配失败
pa_last = La.elem + La.length -1;
pb_last = Lb.elem + Lb.length -1;
while(pa <= pa_last && pb <= pb_last){ //归并
if( *pa <= *pb) *pc++ = *pa++;
else *pc++ = *pb++;
}
while(pa <= pa_last) *pc++ = *pa++;
while(pb <= pb_last) *pc++ = *pb++;
} //MergeList_Sq