一道区间dp和一道字符串

牛X网测试rating系统，叶神开的bnu的重现赛，送8个T恤，就做了两个题参与下抽奖，打了三场了，不出意料的都没抽中我 =-=

 第一道：

小Q同学为了准备今年的ICPC Regional，计划在天之内刷掉道题，每道题有一个难度值，其中第道题的难度值为。

然而处于半颓废状态中的小Q同学不希望在同一天中做难度差距悬殊的题目，定义第天中刷的题的难度的最大值减最小值为（如果第天没有刷题，则），那么整个计划的难度为。

小Q同学可以按照任意的顺序刷题，并且一天中可以刷任意多道题，但是每道题只需要做一次，现在小Q同学想知道完成这个计划的总难度的最小值是多少。

 

Input

第一行是一个正整数，表示测试数据的组数，

对于每组测试数据，

第一行是两个整数和，表示题数和天数，

第二行是个整数，表示每道题的难度值。

 

Output

对于每组测试数据，输出一个整数，表示整个计划的最小难度。

 

Sample Input

2
3 3
1 2 3
3 2
1 2 3

Sample Output

0
1

Hint

对于第一组样例，最优方案是一天刷一题。

对于第二组样例，一个最优方案是第一天刷难度值为1和2的题，第二天刷难度值为3的题。

区间dp了，天数就是区间个数，每天的难度就是一个区间的最大最小差的平方，

求差值平方最小，所以难度相近的一起做，排好序，只要找到已排序的所有题如何分割为m份即可。

这里时限5s很宽，直接三重暴力即可：

dp[i][j]表示前i天做j题的最小难度

新加入第j道题的时候，再加一重循环，遍历前状态中每道题，组成新的区间

dp[i][j] = min(dp[i][j],dp[i-1][k-1]+abs(a[j]-a[k])*abs(a[j]-a[k])); j和k为新的区间

参考数据 2 4 6 8  2天完成 可以 2 4一天 6 8 一天 结果8

　　　　　　　　　　　　也可以 2 4 6 一天 8一天 结果16 

显然 新加入的8找6组成区间值更小一些，再加上 dp[1][2]也就是1天做 2 4道题的状态 是最优值

当然可以用斜率DP优化到二维，

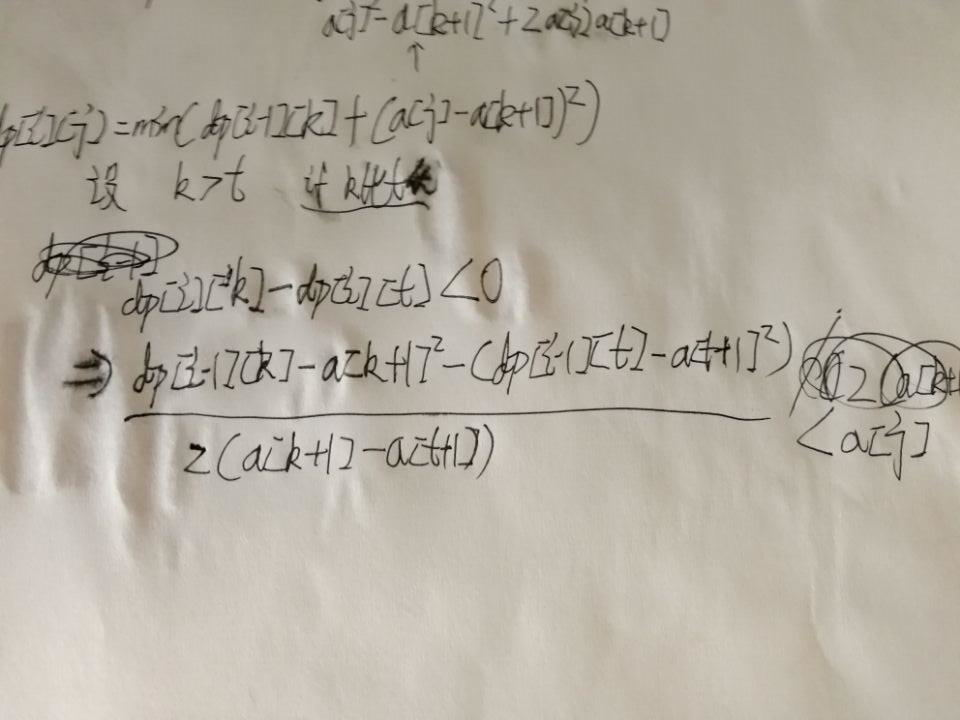
可以说是斜率优化dp的水题，找个好的模板把那几个函数改下也可以

注意初始化那里一般int的已经不行了，普通的4个3f要改成long long的8个3f，还有就是30行必须提前初始化，在转移方程里比较dp[i-1][j]会出现无限大比较无限大的错误

 1 #include <bits/stdc++.h>
 2 typedef long long ll;
 3 
 4 const ll INF = 0x3f3f3f3f3f3f3f3f;//这里必须要设置超过int的，不然WA，后台数据硬
 5 const int N = 500+10;
 6 using namespace std;
 7 int n,m,sum,res,flag;
 8 long long a[N],dp[N][N];
 9 void init()
10 {
11     for(int i=1;i<=n;i++)
12         dp[0][i]=INF;//这种情况是无限大的
13     dp[0][0] = 0;
14 }
15 int main()
16 {
17 //    freopen("in.txt","r",stdin);
18     int i,j,k,cas,T,t,x,y,z;
19     scanf("%d",&T);
20     cas=0;
21     while(T--)
22     {
23         scanf("%d%d",&n,&m);
24         init();
25         for(i=1;i<=n;i++)scanf("%lld",&a[i]);
26         sort(a+1,a+1+n);
27         for(i=1;i<=m;i++)
28             for(j=1;j<=n;j++)
29             {
30                 dp[i][j] = dp[i-1][j];
31                 for(k=1;k<=j;k++) {
32 
33 //                    printf("dp[%d][%d]:%d
",i,j,dp[i][j]);
34 //                    cout<<"dp[i-1][k-1]+abs(a[j]-a[k])*abs(a[j]-a[k]): "<<dp[i-1][k-1]+abs(a[j]-a[k])*abs(a[j]-a[k])<<endl;
35                     dp[i][j] = min(dp[i][j],dp[i-1][k-1]+abs(a[j]-a[k])*abs(a[j]-a[k]));
36 //                    printf("前%d天做%d道题的最小难度是%d
",i,j,dp[i][j]);
37                 }
38             }
39         printf("%lld
",dp[m][n]);
40     }
41     return 0;
42 }

又到了一年一度的北京师范大学程序设计竞赛！本次比赛的负责人萌萌哒whalyzh同学要给大家发比赛账号。由于参赛队伍众多，面对长长的参赛名单，whalyzh同学表示压力山大。现在whalyzh同学实在忙不过来，就扔了一份参赛队伍的账号列表给你。为了确定给校内队伍颁发的各类奖项的名额，他需要知道一共有多少支校内队伍参加了比赛。

 

Input

第一行是一个正整数，表示测试数据的组数，

对于每组测试数据，

第一行是一个整数，表示队伍数量，

接下来行，每行是一个格式为"学校英文名缩写16-队伍编号"的字符串，表示队伍账号，保证学校英文名缩写只包含小写字母，编号是正整数且不含前导零，同一学校不同队伍的编号一定不同，来自不同学校的队伍的编号可能相同。

更多信息请参考样例。

 

Output

对于每组测试数据，输出一行，包含一个整数，表示参赛列表中本校（即学校英文名缩写是"bnu"的队伍）队伍的数量。

 

Sample Input

2
10
bac16-1
bit16-1
bitss16-1
bjfu16-1
bjtu16-1
bnu16-1
buaa16-1
cuc16-1
cugb16-1
google16-1
5
bnu16-1
bnu16-3
bnu16-5
bnu16-2
bnu16-4

Sample Output

1
5

Hint

对于第一组样例，只有"bnu16-1"是校内队伍。

对于第二组样例，所有队伍都是校内队伍。

直接找到bnu的队伍set去重即可，map标记也可以，q神说有小坑，但是不知道在哪里=-=

#include <iostream>
#include <set>
#include <cstdio>
#include <cstring>

using namespace std;
set<string> co;
int main()
{
//    freopen("in.txt","r",stdin);
    int T;
    cin>>T;
    while(T--) {
        co.clear();
        int n;
        cin>>n;
        for(int i = 0; i < n; i++) {
        string s;
        cin>>s;
        if(s.substr(0,6)=="bnu16-") {
            co.insert(s);
            }
        }
        cout<<co.size()<<endl;
    }
    return 0;
}