这个问题是在网易公开课上看到的,传送门:http://open.163.com/movie/2016/7/4/U/MBQOS0ID9_MBQOSMH4U.html
问题描述:
有100个灯泡,编号为1~n,开始都是灭的off状态,在第i回合按下所有编号为i倍数的的开关,灯泡转换一次状态,100回合,问最后有多少灯泡是on亮着的?
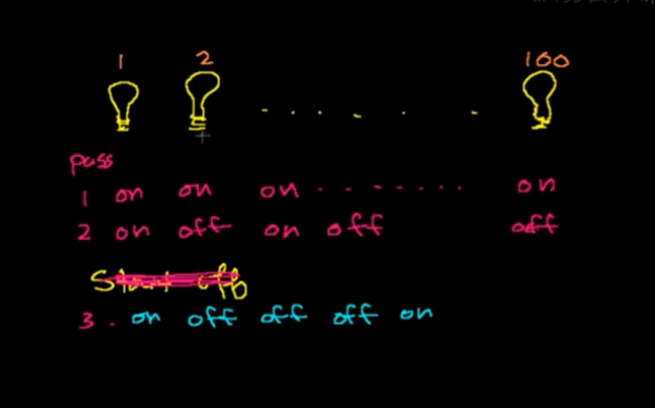
问题解析:
提示:每一轮我们按了什么编号呢?
回合和编号有什么关系?
结果:
如果当前回合是该灯泡编号的因数,该灯泡一定会被按。回合数范围是0~100,那么问题也就转换成了:
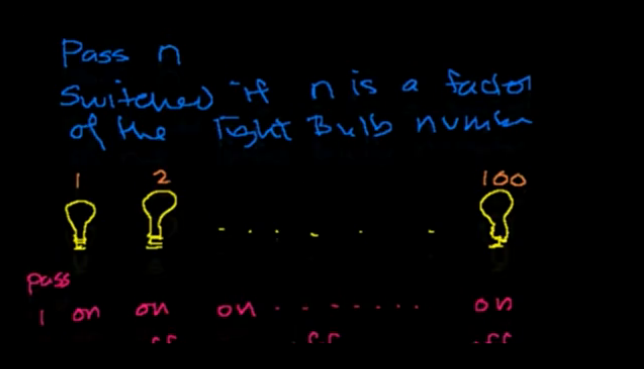
例如:
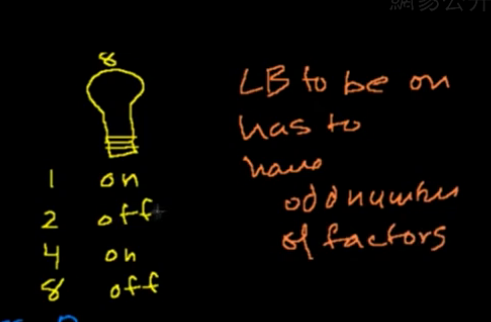
编号8号等,它的因数有1,2,4,8,那么它将在1,2,4,8回合会被按一次,结果最后还是off状态,因为因数的个数为偶数次。
结论:
所以最终也就变成了找灯泡编号的因数有奇数个的个数,因数都是成对出现的,只有完全平方数,最后一个对是相同的,那么就找1~n,i^2小于100即可。
那么就有 1 4 9 16........81 100.
观察这些数的分布:
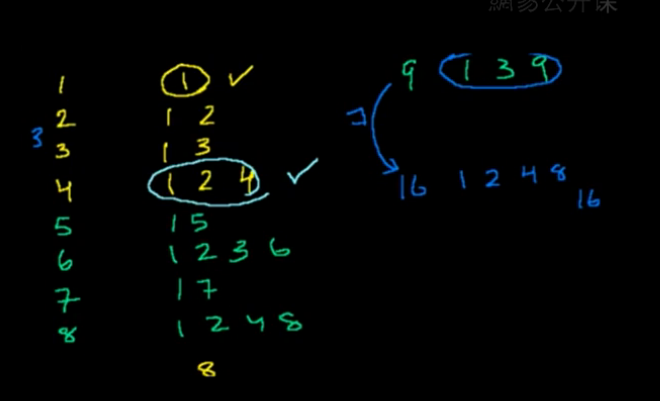
相差成奇数递增间隔的分布,1到4,4到9,9到16,分别隔3,5,7.
Over..............