ZOJ4097 Rescue the Princess（并查集+tarjan双连通分量缩点+LCA倍增算法）

题意：

给出一个无向图，每个询问给出三个点u,v,w，询问能否从v和w找到通往u的路径，且两条路径没有重合的地方。

题解：

图不一定连通，当v,w有任何一个跟u不在一个连通块上，那就直接输出No（用并查集判断）

然后用tarjan算法缩点，每个双连通分量为一个点，建立一个新的图，由于图不一定连通，可以看作是森林。

对森林里的每棵树都做一遍LCA预处理，对于之后每个询问分类讨论，有以下三种合法的情况：

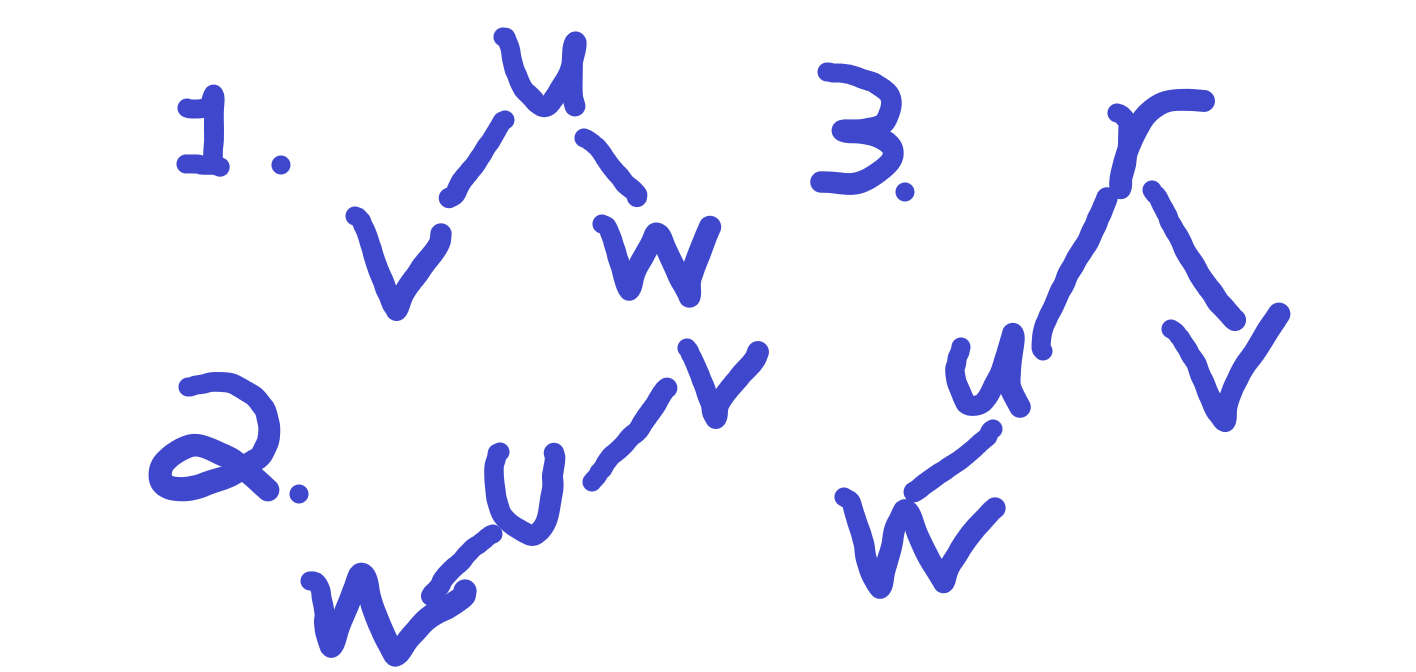
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+14;
int N,M,Q;
int father[30][maxn];
int h[maxn];
vector<int> g[maxn];//原图
vector<int> sc[maxn];//tarjan以后的缩点图 
//倍增求LCA 
int visit[maxn];
void dfs (int x,int u) {
    visit[x]=1;
    h[x]=h[u]+1;
    father[0][x]=u;
    for (int i=1;(1<<i)<=h[x];i++) 
        father[i][x]=father[i-1][father[i-1][x]];
    for (int i=0;i<sc[x].size();i++) {
        int v=sc[x][i];
        if (v==father[0][x]) continue;
        dfs(v,x);
    }
}
int lca (int x,int y) {
    if (h[x]>h[y]) swap(x,y);
    for (int i=20;i>=0;i--) 
        if (h[x]<=h[y]-(1<<i)) y=father[i][y];
    if (x==y) return x;
    for (int i=20;i>=0;i--) {
        if (father[i][x]!=father[i][y]) {
            x=father[i][x];
            y=father[i][y];
        }
    }
    return father[0][x];
}
//并查集判断连通块 
int f[maxn];
int findfather (int x) {
    int a=x;
    while (x!=f[x]) x=f[x];
    while (a!=f[a]) {
        int z=a;
        a=f[a];
        f[z]=x;
    }
    return x;
}
void Union (int a,int b) {
    int faA=findfather(a);
    int faB=findfather(b);
    if (faA!=faB) f[faA]=faB;
}
//tarjan双连通分量缩点
int low[maxn];
int dfn[maxn];
int pos[maxn];
int scc=0;
int cnt;
stack<int> st;
void tarjan (int x,int pre) {
    low[x]=dfn[x]=++cnt;
    st.push(x);
    int son=0;
    for (int i=0;i<g[x].size();i++) {
        if (g[x][i]==pre&&++son<2) continue;
        if (!low[g[x][i]]) {
            tarjan(g[x][i],x);
            low[x]=min(low[x],low[g[x][i]]);
        }
        else if (!pos[g[x][i]]) 
            low[x]=min(low[x],dfn[g[x][i]]);
    }
    if (low[x]==dfn[x]) {
        scc++;
        while (1) {
            int u=st.top();
            st.pop();
            low[u]=low[x];
            pos[u]=scc;
            if (u==x) break;
        }
    }
} 

//建立缩点图
void build_sc () {
    for (int i=1;i<=N;i++) {
        for (int j=0;j<g[i].size();j++) 
            if (pos[i]!=pos[g[i][j]])
                sc[pos[i]].push_back(pos[g[i][j]]);
    }
} 
int main () {
    int T;
    scanf("%d",&T);
    while (T--) {
        scanf("%d%d%d",&N,&M,&Q);
        for (int i=1;i<=N;i++)
            g[i].clear(),f[i]=i,sc[i].clear();
        memset(father,0,sizeof(father));
        memset(h,0,sizeof(h));
        memset(visit,0,sizeof(visit));
        scc=0;
        cnt=0;
        fill(low,low+maxn,0);
        fill(dfn,dfn+maxn,0);
        fill(pos,pos+maxn,0);
        while (!st.empty()) st.pop();
        for (int i=0;i<M;i++) {
            int x,y; 
            scanf("%d%d",&x,&y);
            g[x].push_back(y);
            g[y].push_back(x);
            Union(x,y);
        }
        for (int i=1;i<=N;i++) 
            if (!dfn[i]) tarjan(i,i);
        build_sc(); 
        for (int i=1;i<=scc;i++) 
             if (!visit[i]) dfs(i,i);
        for (int i=0;i<Q;i++) {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            int faU=findfather(u);
            int faV=findfather(v);
            int faW=findfather(w);
            u=pos[u];
            v=pos[v];
            w=pos[w];
            //printf("%d %d %d
",u,v,w);
            if (faU!=faV||faU!=faW) {
                printf("No
");
                continue;
            }
            int flag=1;
            int uv=lca(u,v);
            int uw=lca(u,w);
            int vw=lca(v,w);
            if (uv==u) {
                if (uw==u&&vw==u) flag=1;
                else if (uw!=u) flag=1;
                else flag=0;
            }
            else if (uv==v) {
                if (uw==u) flag=1;
                else flag=0;
            }
            else {
                if (uw!=u) flag=0;
            }
            if (flag) printf("Yes
");
            else printf("No
");
        }
    } 
    return 0;
}