我说这是我们的noip互测题你信吗...
首先介绍一下仙人掌(略,参见题面)
然后我们思考一下怎么做:
首先,如果原图是一棵树,那么做法是很显然的(树上最长链嘛)
但是,图是一个仙人掌,所以树上最长链的做法有bug
所以我们考虑:是否能将树上的做法移接到仙人掌上即可
怎么移接?
我们看到,根据仙人掌的性质,如果我们对这个仙人掌搜出一棵dfs树,那么不在环上的边一定是树边
如果换一种说法,那么这种边一定是割边!
所以,如果我们把仙人掌看做树上挂着环的一种图,那么我们是可以套用树上最长链的思想,配合树形dp来解决这道题的!
举个例子:
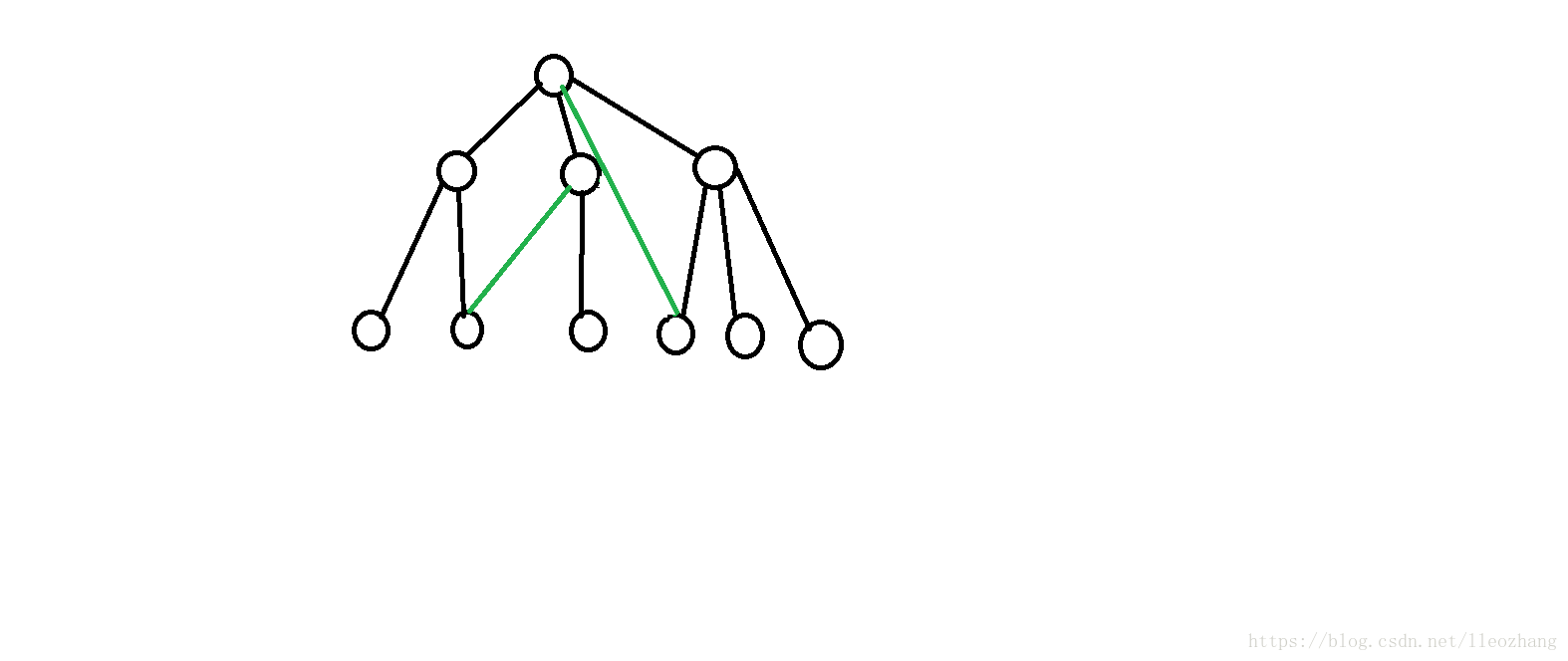
这是一棵很典型的树
现在我引入了两条绿色的边(非树边),他就变成了一个典型的仙人掌
于是我们可以对这个仙人掌进行tarjan(很显然,它是有环的,不是吗?)
在tarjan的同时,我们对树边进行树形dp
记dp[i]表示以i为根节点且一定经过i的子树中的以i为起点的最长链长度
于是我们显然有转移:,其中to为i的一个子节点
可是由于它是一个仙人掌,所以存在环,我们知道,对于环,树形dp是处理不了的啊
所以我们借助tarjan进行缩点,分别处理环内和环外的点
方式:对每个点记录一个树上父节点,那么如果从某个点能直接连通到另一个点,但这个点却不是那个点的树上儿子,则说明这两点之间一定存在一个环!
(这一点很显然,对照图理解一下就好)
接下来,在环内我们需要单独处理一遍dp
处理方式待会再说
于是这道题就被分成了两部分:
①:对树部分进行dfs树形dp
②:对环部分单独dp
在树部分,结合上面提到的转移,我们有:
(更新答案是很显然的,因为我可没有要求答案的起点一定是u,所以自然是两条以u为起点的链通过u连起来比较长)
至于环内部分,结合我们刚才提到的判环条件,我们能很清楚的发现一件事情:
①:对于一个环内点的dp值只会影响环内点,而不会影响环外点(环外点与环内点是通过树边进行更新,不涉及环的问题)
②:但是上面这句话存在漏洞:要求这个环内点并不是环中的最高点才行!
为什么?
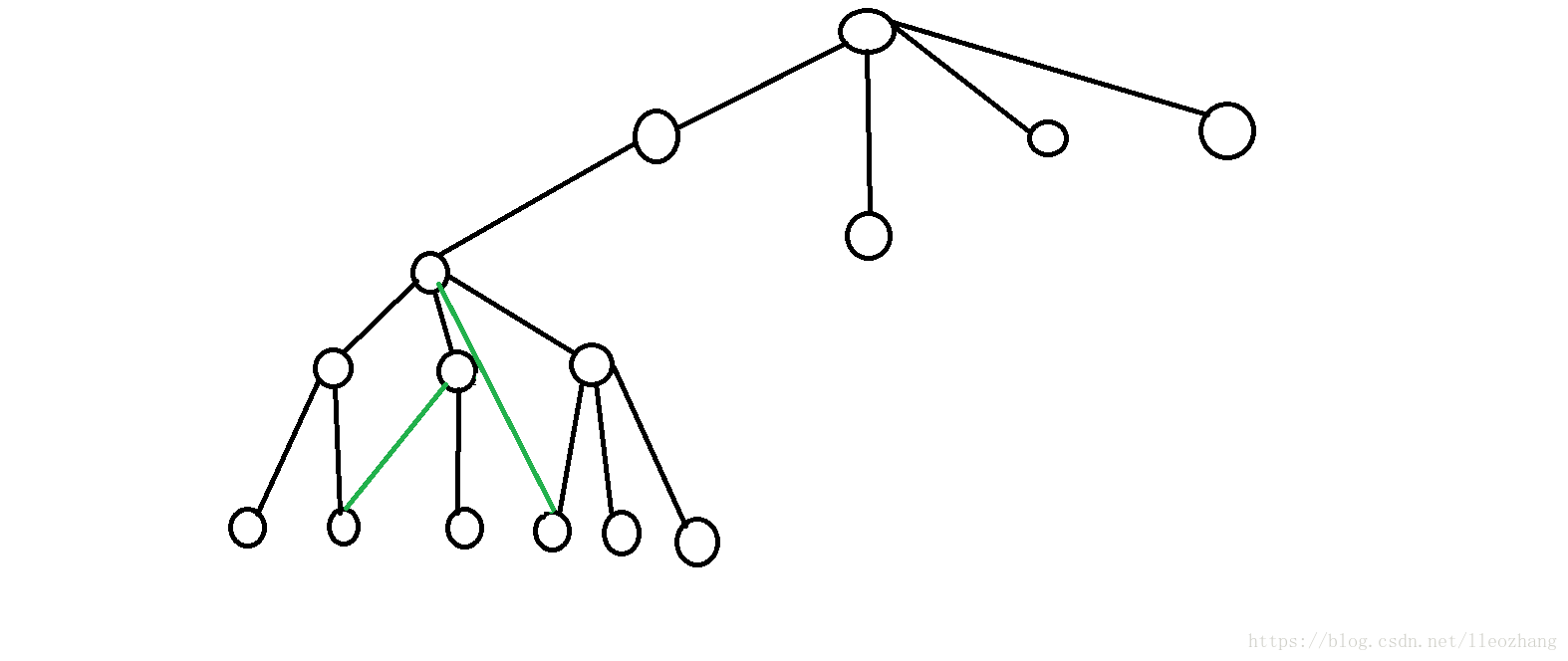
例:
观察一下,我们能看到:底下绿色的环的dp值只有最上面的那个点才回涉及到对上半部分dp值的更新,而剩下的是没有用的
所以我们在处理每个环时,仅需处理深度最浅的点,更新他的dp值即可
但是,每个点的dp值都会对答案有贡献,因此不要忘记更新答案!
接下来的问题就好说了:如果我们记环中最高点为u,那么根据上述提到的找环的方法,我们完全可以:找到u的一个to,反复找到to的父节点,根据u为环中最高点这一性质,我们最终一定能跳到u,而所有遍历到的点就是一整个环!
在更新答案时,显然我们要找到换上两点i,j,使得dp[i]+dp[j]+dis(i,j)最大来更新ans
朴素来看,这将是个O(n^2)算法
但是我们可以利用单调队列进行优化,因为dis(i,j)根据遍历环的顺序直接可求
这样就优化成了O(n)
最后更新一遍环上最高点的dp值即可。
#include <cstdio> #include <cmath> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> #include <queue> #include <stack> using namespace std; struct Edge { int next; int to; }edge[300005]; int head[100005]; int dfn[100005]; int dep[100005]; int low[100005]; int f[100005]; int dp[100005]; int sta[100005],que[100005]; int tot,deep; int cnt=1; int n,m; int ans=0; void init() { memset(head,-1,sizeof(head)); cnt=1; } void add(int l,int r) { edge[cnt].next=head[l]; edge[cnt].to=r; head[l]=cnt++; } void dpit(int ed,int st) { int cct=0; while(st!=ed) { sta[++cct]=dp[st]; st=f[st]; } sta[++cct]=dp[ed]; for(int i=1;i<cct;i++) { sta[i+cct]=sta[i]; } int head=1,tail=1; que[1]=1; for(int i=2;i<=cct+cct/2;i++) { while(head<=tail&&i-que[head]>cct/2) { head++; } ans=max(ans,sta[i]+sta[que[head]]+i-que[head]); while(head<=tail&&sta[que[tail]]+i-que[tail]<=sta[i]) { tail--; } que[++tail]=i; } for(int i=1;i<cct;i++) { dp[ed]=max(dp[ed],sta[i]+min(i,cct-i)); } } void tarjan(int rt) { dfn[rt]=low[rt]=++deep; for(int i=head[rt];i!=-1;i=edge[i].next) { int to=edge[i].to; if(to==f[rt]) { continue; } if(!dfn[to]) { f[to]=rt; dep[to]=dep[rt]+1; tarjan(to); low[rt]=min(low[rt],low[to]); if(dfn[rt]<low[to]) { ans=max(ans,dp[rt]+dp[to]+1); dp[rt]=max(dp[rt],dp[to]+1); } }else { low[rt]=min(low[rt],dfn[to]); } } for(int i=head[rt];i!=-1;i=edge[i].next) { int to=edge[i].to; if(f[to]==rt||dfn[to]<=dfn[rt]) { continue; } dpit(rt,to); } } inline int read() { int f=1,x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int main() { // freopen("pianfen.in","r",stdin); // freopen("pianfen.out","w",stdout); n=read(),m=read(); init(); for(int i=1;i<=m;i++) { int k=read(); int las=0; for(int j=1;j<=k;j++) { int x=read(); if(!las) { las=x; continue; } add(x,las); add(las,x); las=x; } } /*for(int i=1;i<=min(n,9871);i++) { int x=read(); if(x!=0&&x!=1) { printf("-l "); return 0; } }*/ tarjan(1); printf("%d ",ans); return 0; }