题意:给出两个字符串,求这两个子串中最长相同子串长度
策略:
首先,我们可以将这两个字符串首尾相接,这样我们就可以获得一个长字符串,然后我们对这个新串求出height数组,然后枚举所有height并且找出两个sa,查出这两个sa是否在两个串内,这样就可以了如果是的话就用height更新ans即可
还有一个细节要注意(虽然没写也能A,但总归是个hack点啊)
状况如下:
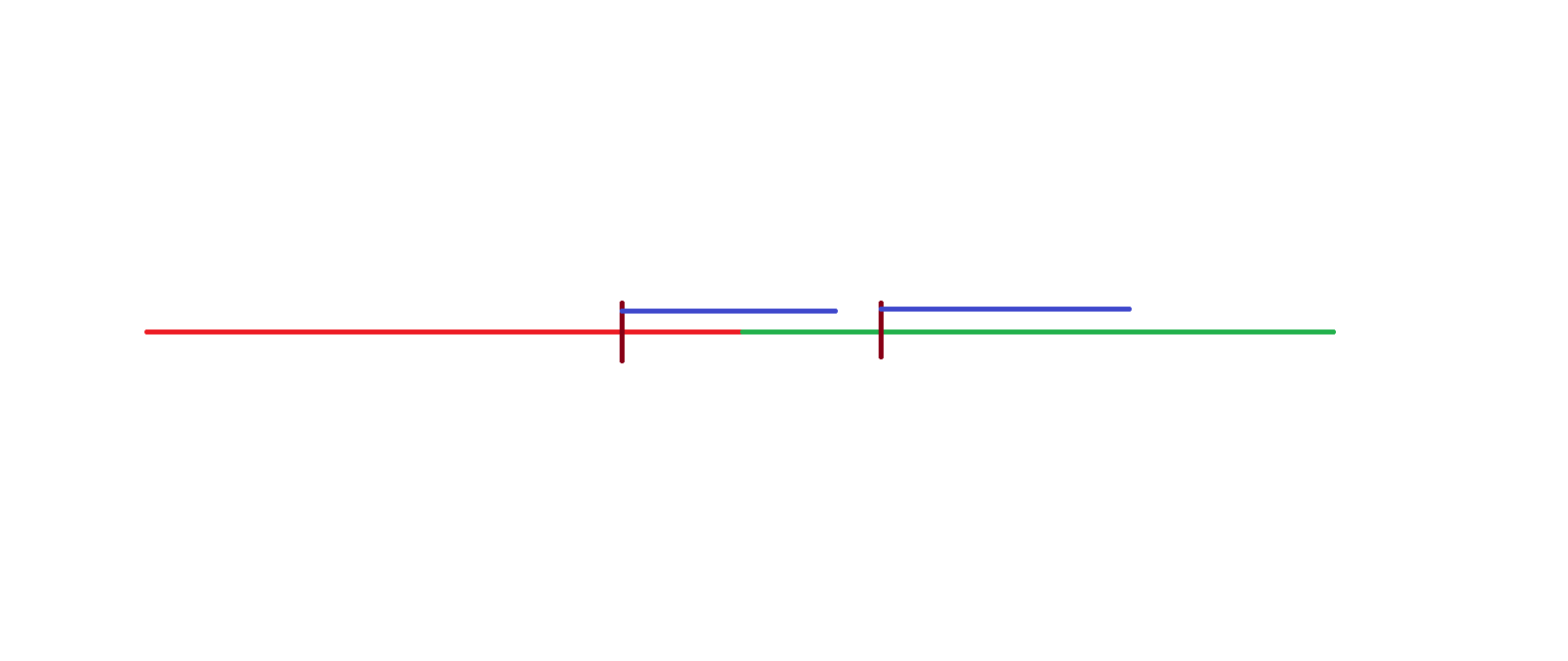
如图所示,下面的红色和绿色是两个字符串,两个褐色位置是sa[i]和sa[i-1],而蓝色部分就是height值
所以问题体现在上面了:如果两个前缀相同,但某一个前缀越过了分界线怎么办?
所以我们在分界线上插入一个无关字符(如‘#’),这样的话height在求的时候是无论如何不会越过分界线的
这样就可以了
代码:
#include <cstdio> #include <cmath> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> #include <queue> #include <stack> using namespace std; int sa[200010]; char s[200010]; int height[200010]; int rank[200010]; char t1[100005]; int f1[200010]; int f2[200010]; int f3[200010]; int has[200010]; int l,m=127; void turnit() { memcpy(f3,f1,sizeof(f3)); memcpy(f1,f2,sizeof(f1)); memcpy(f2,f3,sizeof(f2)); } void get_sa() { for(int i=1;i<=l;i++) { f1[i]=s[i]; has[f1[i]]++; } for(int i=2;i<=m;i++) { has[i]+=has[i-1]; } for(int i=l;i>=1;i--) { sa[has[f1[i]]--]=i; } for(int k=1;k<=l;k<<=1) { int tot=0; for(int i=l-k+1;i<=l;i++) { f2[++tot]=i; } for(int i=1;i<=l;i++) { if(sa[i]>k) { f2[++tot]=sa[i]-k; } } for(int i=1;i<=m;i++) { has[i]=0; } for(int i=1;i<=l;i++) { has[f1[i]]++; } for(int i=2;i<=m;i++) { has[i]+=has[i-1]; } for(int i=l;i>=1;i--) { sa[has[f1[f2[i]]]--]=f2[i]; f2[i]=0; } turnit(); f1[sa[1]]=1; tot=1; for(int i=2;i<=l;i++) { if(f2[sa[i]]==f2[sa[i-1]]&&f2[sa[i]+k]==f2[sa[i-1]+k]) { f1[sa[i]]=tot; }else { f1[sa[i]]=++tot; } } if(tot==l) { break; } m=tot; } for(int i=1;i<=l;i++) { rank[sa[i]]=i; } int f=0; for(int i=1;i<=l;i++) { if(rank[i]==1) { continue; } if(f) { f--; } int j=sa[rank[i]-1]; while(s[i+f]==s[j+f]) { f++; } height[rank[i]]=f; } } int main() { scanf("%s",t1+1); int l1=strlen(t1+1); l+=l1; for(int i=1;i<=l1;i++) { s[i]=t1[i]; } scanf("%s",t1+1); l++; s[l]='#'; int l2=strlen(t1+1); l+=l2; for(int i=l-l2+1;i<=l;i++) { s[i]=t1[i-l1-1]; } get_sa(); int ans=0; for(int i=2;i<=l;i++) { int e1=sa[i]; int e2=sa[i-1]; if(e1>e2) { swap(e1,e2); } if(e1<=l1&&e2>l1) { ans=max(ans,height[i]); } } printf("%d ",ans); return 0; }