poj 1743

激动ing...我完成了1/8的男人...

其实不难，但我交了3页WA，原因是我为防RE特判n=1直接输出，并没有读入！！！

题意：给定一个长为n的序列，定义该序列的两个子序列（连续）相似，当且仅当这两个子序列长度相同且互不重叠，而且这两个子序列每个序列内部相邻元素前后做差，将所有差值排列成一个序列，这两个子序列得出的序列完全相同，现在想求这样的子序列最长的长度

举个例子：序列1 2 5和4 5 8是相似的，因为做差后的序列都是1 3

然后我们考虑怎么解决这个问题

主体思想：后缀数组+二分答案

其实有个思想是显然的，就是对于原序列两两做差，那么问题会简化成求一个序列中完全相同且互不相交的两个子段最长有多长

利用后缀数组优秀的性质，我们可以求出一个height数组，其中height[i]表示排名为i和i-1的两个后缀的最长公共前缀长度

至于height数组怎么求，可以参考网上其他博客，这里先略过

我们重点谈一谈如何利用height数组的性质解决本题

首先，我们可以二分答案，即二分可能的长度

然后我们进行检验：

设二分的答案为v

枚举字符串的排名（由于排名为1的字符串height为0，所以可以从2开始），然后检验他的height值，如果我们有长度超过v的一段height值大于等于v，那么就是合法的

原因：

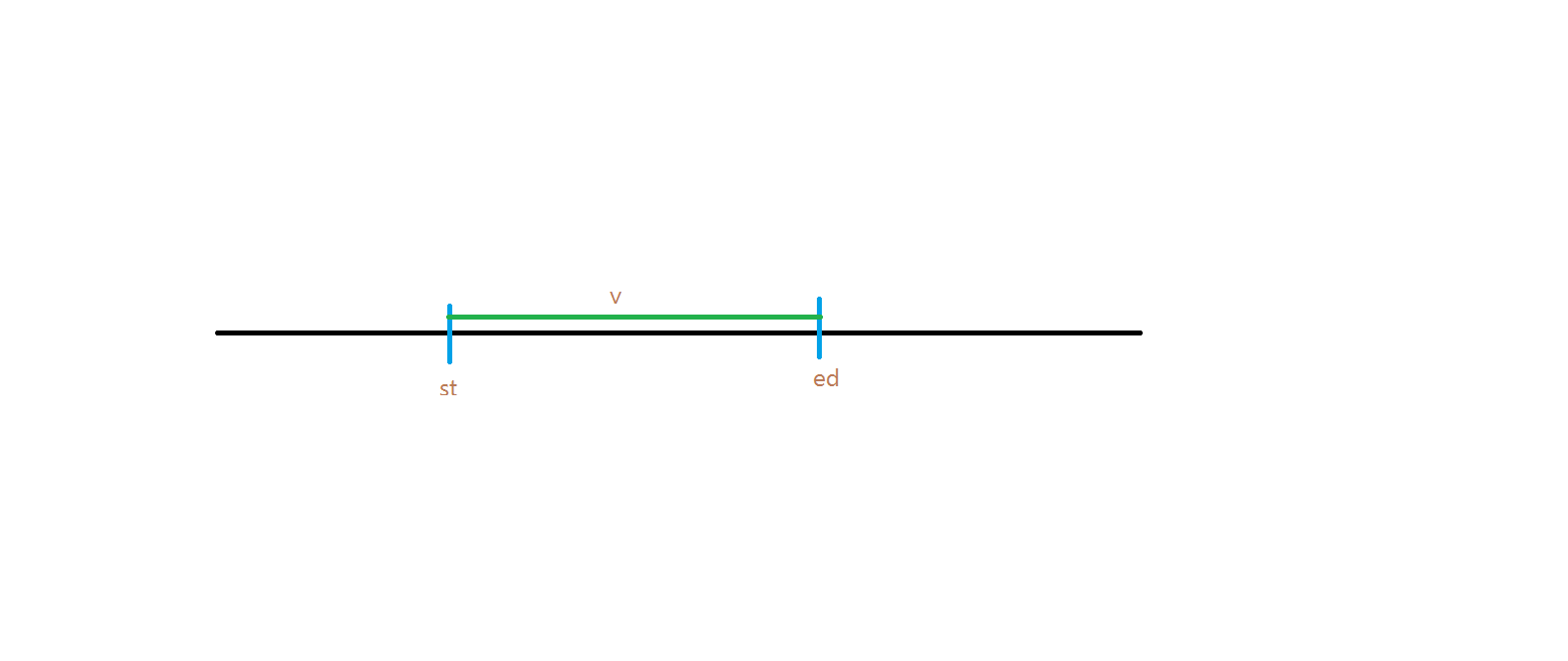
如图所示，如果我们有从st到ed的一段height值都>=v，而且ed-st>v，那么我们一定能找到一个以st为起点和以ed为起点的，长度为v的子段相同

这样也就实现了检验

代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
int sa[30005];
int heit[30005];
int rank[30005];
int f1[30005];
int f2[30005];
int f3[30005];
int a[30005];
int s[30005];
int has[30005];
int l,m=200;
void turnit()
{
    memcpy(f3,f1,sizeof(f3));
    memcpy(f1,f2,sizeof(f1));
    memcpy(f2,f3,sizeof(f2));
}
void init()
{
    memset(sa,0,sizeof(sa));
    memset(has,0,sizeof(has));
    memset(s,0,sizeof(s));
    memset(a,0,sizeof(a));
    memset(heit,0,sizeof(heit));
    memset(rank,0,sizeof(rank));
    memset(f1,0,sizeof(f1));
    memset(f2,0,sizeof(f2));
    memset(f3,0,sizeof(f3));
}
void get_hei()
{
    int f=0;
    for(int i=1;i<=l;i++)
    {
        if(rank[i]==1)
        {
            continue;
        }
        int j=sa[rank[i]-1];
        if(f)
        {
            f--;
        }
        while(s[i+f]==s[j+f])
        {
            f++;
        }
        heit[rank[i]]=f;
    }
}
void get_sa()
{
    for(int i=1;i<=l;i++)
    {
        f1[i]=s[i];
        has[f1[i]]++;
    }
    for(int i=2;i<=m;i++)
    {
        has[i]+=has[i-1];
    }
    for(int i=l;i>=1;i--)
    {
        sa[has[f1[i]]--]=i;
    }
    for(int k=1;k<=l;k<<=1)
    {
        int tot=0;
        for(int i=l-k+1;i<=l;i++)
        {
            f2[++tot]=i;
        }
        for(int i=1;i<=l;i++)
        {
            if(sa[i]>k)
            {
                f2[++tot]=sa[i]-k;
            }
        }
        for(int i=1;i<=m;i++)
        {
            has[i]=0;
        }
        for(int i=1;i<=l;i++)
        {
            has[f1[i]]++;
        }
        for(int i=1;i<=m;i++)
        {
            has[i]+=has[i-1];
        }
        for(int i=l;i>=1;i--)
        {
            sa[has[f1[f2[i]]]--]=f2[i];
            f2[i]=0;
        }
        turnit();
        f1[sa[1]]=1;
        tot=1;
        for(int i=2;i<=l;i++)
        {
            if(f2[sa[i]]==f2[sa[i-1]]&&f2[sa[i]+k]==f2[sa[i-1]+k])
            {
                f1[sa[i]]=tot;
            }else
            {
                f1[sa[i]]=++tot;
            }
        }
        if(tot==l)
        {
            break;
        }
        m=tot;
    }
    for(int i=1;i<=l;i++)
    {
        rank[sa[i]]=i;
    }
    get_hei();
}
bool check(int v)
{
    int minx=0x3f3f3f3f;
    int maxx=-0x3f3f3f3f;
    for(int i=2;i<=l;i++)
    {
        if(heit[i]>=v)
        {
            minx=min(minx,min(sa[i],sa[i-1]));
            maxx=max(maxx,max(sa[i],sa[i-1]));
            if(maxx-minx>v)
            {
                return 1;
            }
        }else
        {
            minx=0x3f3f3f3f;
            maxx=-0x3f3f3f3f;
        }
    }
    return 0;
}
void divi()
{
    int lq=0,rq=l/2;
    int ans;
    while(lq<=rq)
    {
        int mid=(lq+rq)>>1;
        if(check(mid))
        {
            ans=mid;
            lq=mid+1;
        }else
        {
            rq=mid-1;
        }
    }
    if(ans<4)
    {
        printf("0
");
    }else
    {
        printf("%d
",ans+1);
    }
}
int main()
{
//    freopen("data.txt","r",stdin);
    while(1)
    {
        scanf("%d",&l);
        if(l==0)
        {
            return 0;
        }
        init();
        for(int i=1;i<=l;i++)
        {
            scanf("%d",&a[i]);
        }
        if(l==1)
        {
            printf("0
");
            continue;
        }
        l--;
        for(int i=1;i<=l;i++)
        {
            s[i]=a[i+1]-a[i]+100;
        }
        m=200;
        get_sa();
        divi();
    }
    return 0;
}