背景与原理:
支持向量机是一种用来解决分类问题的算法,其原理大致可理解为:对于所有$n$维的数据点,我们希望能够找到一个$n$维的直线(平面,超平面),使得在这个超平面一侧的点属于同一类,另一侧的点属于另一类。而我们在寻找这个超平面的时候,我们只需要找到最接近划分超平面的点,而一个$n$维空间中的点等同于一个$n$维向量,所以这些点就可以被称为支持向量。
在一个$n$维空间中,一个超平面可以用$0=w^{T}x+b$表示,比如一条二维空间中的直线可以表示成$ax+by+c=0$,而一个三维空间中的平面可以表示成$ax+by+cz+d=0$,以此类推。而$n$维空间的一个超平面会把$n$维空间中的点分成三部分:对一个$n$维空间中的点$x_{0}$和超平面$w^{T}x+b=0$,若$w^{T}x_{0}+b<0$,说明$x_{0}$在超平面的一侧,而若$w^{T}x_{0}+b=0$,说明$x_{0}$在超平面上,若$x^{T}x_{0}+b>0$,说明$x_{0}$在超平面的另一侧,也就是说,当我们给定了一个超平面之后,空间中的所有点就自然被这个超平面分成了两类(如果忽略超平面上的点)
线性可分支持向量机:
首先我们考虑线性可分的点,即客观存在一个超平面,使得两类数据点分别分布在超平面的两侧,那么不难想见,这样的超平面有无穷多个,但为了模型的泛化性能,我们希望选取的超平面应该是位于两组数据集中间的(个人理解:考虑一种极端情况:这个超平面是贴着某一类的数据点经过的,那么在实际情况中,属于这类的数据点很可能有些稍微散布到了这条直线外,这样这个分类器的性能就不够好了,而如果位于中间,即使有些数据点相较于训练数据有些往外散布,也能较为正确地分类。)
那么由计算几何中的已知公式,我们可以看到:$n$维空间中任意一个点$x_{0}$到一个给定超平面$w^{T}x+b=0$的距离为$\dfrac{|w^{T}x_{0}+b|}{|w|}$,其中$|w|=\sqrt{\sum_{i=1}^{n}w_{i}^{2}}$。而假设对于第$i$组数据,其类别为$y_{i}$,由于我们要根据数据点在超平面的哪一侧确定类别,因此我们实际是要求数据点的位置与数据点的类别相匹配,那么我们的类别也非常自然地选取1/-1,而是否匹配则可以由$y_{i}(w^{T}x_{i}+b)$的正负性来度量,如果为正我们认为是相匹配的。
那么这个问题就变成了:对于一组数据$(X_{1},y_{1}),...,(X_{m},y_{m})$,其中$X_{i}$是$n$维向量,我们要求一个$n$维超平面$w^{T}x+b=0$,而如果令$r=min_{i=1}^{m}\dfrac{|w^{T}X_{i}+b|}{|w|}$,那么我们要最大化$r$,而约束条件则是$y_{i}\dfrac{w^{T}X_{i}+b}{|w|}\geq r$(这个约束条件有点唬人:$y$的取值只有1/-1,所以$y$不影响左边这个东西的绝对值,而$r$一定小于等于左边这个东西的绝对值,因此这个约束条件实际只约束了符号)
那么令$w=\dfrac{w}{|w|r},b=\dfrac{b}{|w|r}$(这并不影响超平面),这样就得到了约束条件:$y_{i}(w^{T}X_{i}+b)\geq 1$(对超平面的所有参数除以同一个值并不改变这个超平面,只是让约束条件更好看了)
而在这个约束条件下,我们可以看到$|w^{T}X_{i}+b|\geq 1$,于是$r \leq \dfrac{1}{|w|}$(由$r$的定义立得),于是我们实际上要最大化的是$\dfrac{1}{|w|}$,那么也就是最小化$|w|$,而这不好求解,所以我们要求最小化$\dfrac{1}{2}|w|^{2}$(这些变化都是为了计算简便)
这样我们的问题就转化为了:在$y_{i}(w^{T}X_{i}+b)\geq 1$的条件下,最小化$\dfrac{1}{2}|w|^{2}$
那么这是个条件最值,我们应用拉格朗日乘子法,构造拉格朗日函数:
$L=\dfrac{|w|^{2}}{2}-\sum_{i=1}^{m}\alpha_{i}(y_{i}(w^{T}X_{i}+b)-1)$
这个问题并不好求解,因为参数个数等于数据集大小了,因此我们考虑改进:设$\theta(w)=max_{\alpha_{i}\geq 0}L$
那么可以看到,在所有的约束条件都成立时,后面要减掉的那一项一定非负,这样的话对于所有的$y_{i}(w^{T}X_{i}+b)-1>0$,应该取对应的$\alpha_{i}=0$才能取得最大值,而最后能取得的最大值就是前面那项$\dfrac{|w|^{2}}{2}$,于是此时的$\theta(w)=\dfrac{|w|^{2}}{2}$
而如果有某个约束条件不成立,后面要减掉的那一项是个负值,这样的话对应的$\alpha_{i}$越大,整个函数值越大,这样$\theta(w)=+\infty$
这样的话我们如果我们想在所有约束条件成立的情况下最小化$\dfrac{|w|^{2}}{2}$,我们实际上就是在最小化$\theta(w)$,即我们要进行的是这样的操作:
$min_{w,b}max_{\alpha_{i}\geq 0}L$
而可以证明,这个问题与其对偶问题:
$max_{\alpha_{i}\geq 0}min_{w,b}L$
是等价的,因此我们来解决这个对偶问题:首先我们对$w$和$b$求偏导:
$\dfrac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^{m}\alpha_{i}y_{i}X_{i}$
$\dfrac{\partial L}{\partial b}=0 \Rightarrow \sum_{i=1}^{m}\alpha_{i}y_{i}=0$
这样我们直接代入,可得我们要进行的任务是:
$max_{\alpha_{i}\geq 0}\dfrac{|\sum_{i=1}^{m}\alpha_{i}y_{i}X_{i}|^{2}}{2}-\sum_{i=1}^{m}\alpha_{i}(y_{i}((\sum_{j=1}^{m}\alpha_{j}y_{j}X_{j})X_{i}+b)-1)$
这样实际就是
$max_{\alpha_{i}\geq 0}-\dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}(X_{i}\cdot X_{j})}{2}+\sum_{i=1}^{m}\alpha_{i}$
取个符号变成等价的问题:
$min_{\alpha_{i}\geq 0} \dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}(X_{i}\cdot X_{j})}{2}-\sum_{i=1}^{m}\alpha_{i}$
这样最后的问题就确定了:我们要在$\alpha_{i}$非负的条件下最小化$\dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}(X_{i}\cdot X_{j})}{2}-\sum_{i=1}^{m}\alpha_{i}$,求出最小的$\alpha$后我们就可以计算出:
$w=\sum_{i=1}^{m}\alpha_{i}y_{i}X_{i}$
同时一定存在一个$\alpha_{j}>0$(否则$w=0$),那么对于这个$j$,有:
$y_{j}-w^{T}X_{j}=b$
代入上面求出的$w$,即得到:
$b=y_{j}-\sum_{i=1}^{m}\alpha_{i}y_{i}(X_{i}\cdot X_{j})$
这里有一个逻辑:我们上文已经提到了,对于所有的$y_{i}(w^{T}X_{i}+b)-1>0$,应该取对应的$\alpha_{i}=0$,也就是说只有$y_{i}(w^{T}X_{i}+b)=1$才会产生非零的$\alpha_{i}$,而由于$y_{i}$只能为1/-1,因此移项即得$y_{j}-w^{T}X_{j}=b$。
而这同样也启示我们:训练完成后,大部分样本都不需要保留,支持向量机只与处于边界位置的支持向量有关。
当然了,这并不是线性问题的结束,因为真实生活中,很难存在绝对线性可分的数据,大多数的数据在分割位置上是有交叉的,这样的话上面的理论模型就不好用了。
因此我们退一步,允许有一定的偏移,同时在损失函数中增加一个惩罚项,也即我们要最小化
$\dfrac{|w|^{2}}{2}+C\sum_{i=1}^{m}\xi_{i}$
其中$\xi_{i}=max(0,1-y_{i}(w^{T}X_{i}+b)$表示一个分类错误的程度,而$C$是惩罚系数,$C$越大代表我们对分类错误的惩罚越大。
因此整个算法流程为:
(1)给定训练集$(X_{1},y_{1}),...,(X_{m},y_{m})$,其中$y_{i}=1/-1$,选取惩罚参数$C$
(2)最小化$\dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}(X_{i}\cdot X_{j})}{2}-\sum_{i=1}^{m}\alpha_{i}$,约束条件是$0\leq \alpha_{i} \leq C$和$\sum_{i=1}^{m}\alpha_{i}y_{i}=0$(这个求解过程与无惩罚项的时候类似,这里不展开了)
(3)$w=\sum_{i=1}^{m}\alpha_{i}y_{i}X_{i}$,找到$\alpha_{j}>0$,对于这个$j$,$b=y_{j}-\sum_{i=1}^{m}\alpha_{i}y_{i}(X_{i}\cdot X_{j})$,得到超平面$w^{T}x+b=0$
(4)分类函数即为$f(x)=sgn(w^{T}x+b)$
非线性可分支持向量机:
在现实生活中,很多数据并不是线性可分的,比如二维空间按一个圆内和圆外对点进行分类,这显然不是一个线性可分的问题,那么对于这种问题我们的处理方法是将其映射到更高维度的空间中去,以期在更高维度的空间中其是线性可分的。
但是在上述讨论过程中我们可以看到,我们需要的其实并不是真正的高维空间中的点是什么,我们只需要计算出两个点之间的点积!
那么如果我们设函数$\phi(x)$把$x$投影到高维空间,那我们只需要一个函数$K(x,z)=\phi(x) \cdot \phi(z)$,这样的话我们就只需最小化
$\dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}K(X_{i}, X_{j})}{2}-\sum_{i=1}^{m}\alpha_{i}$
而不需要得知某个$X$投影到高维空间中具体是什么了。
所以我们实际上要选取的是$K$,这个$K$又被称为核函数,常用的核函数有多项式核,高斯核$K(x_{1},x_{2})=e^{-\frac{|x_{1}-x_{2}|^{2}}{2\sigma^{2}}}$和线性核$K(x_{1},x_{2})=x_{1}\cdot x_{2}$(线性核存在的意义是统一了所有的支持向量机的形式,这样无论是什么问题我们都要选取一个核然后操作,而不用根据是否是线性可分选取不同的形式了)
因此所有的支持向量机的算法步骤为:
(1)给定训练集$(X_{1},y_{1},...,(X_{m},y_{m})$,其中$y_{i}=1/-1$,选取惩罚参数$C$和核函数$K$
(2)最小化$\dfrac{\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}K(X_{i}, X_{j})}{2}-\sum_{i=1}^{m}\alpha_{i}$,约束条件是$0\leq \alpha_{i} \leq C$和$\sum_{i=1}^{m}\alpha_{i}y_{i}=0$
(3)找到$\alpha_{j}>0$,对于这个$j$,$b=y_{j}-\sum_{i=1}^{m}\alpha_{i}y_{i}K(X_{i}, X_{j})$,得到超平面$w^{T}x+b=0$
(4)分类函数即为$f(x)=sgn(\sum_{i=1}^{m}\alpha_{i}y_{i}K(X,X_{i})+b)$
代码实现:
import numpy as np import math import matplotlib.pyplot as plt from sklearn import svm x=np.arange(0.,10.,0.02) y=5-2*x/3+np.random.randn(500) now=0 dataset=[] for i in range(0,500): typ = -1 if 2*x[i]+3*y[i] <= 15: if abs(np.random.randn(1)[0])<2: typ = 1 else: typ = -1 else: if abs(np.random.randn(1)[0]) < 2: typ = -1 else: typ = 1 dataset.append([x[i],y[i],typ]) X=(np.array(dataset)[:,0:2]) Y=(np.array(dataset)[:,2]) model=svm.SVC(C=1.0,kernel='linear').fit(X,Y) for i in range(0,500): if Y[i]==1: plt.scatter(X[i,0],X[i,1],c='r') else: plt.scatter(X[i,0],X[i,1],c='b') w=model.coef_ b=model.intercept_ plt.plot(X[:,0],-(w[0][0]/w[0][1])*X[:,0]-b[0]/w[0][1],c='g',linewidth=3) plt.show()
支持向量机的代码不好实现,这里直接调了库,要分类的数据和之前逻辑回归是的是一样的,分类效果如下:
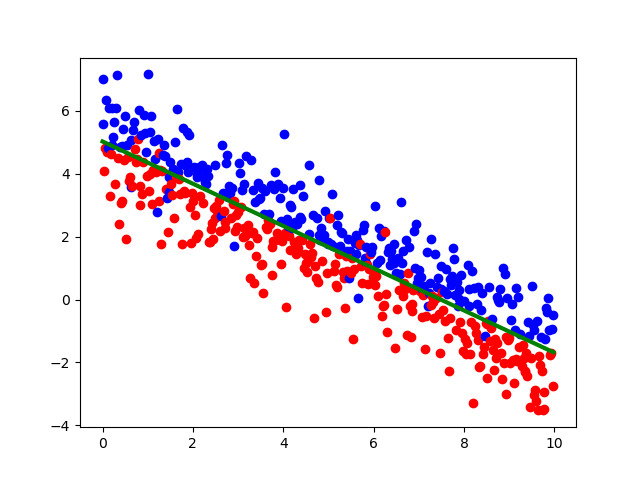
可以看到分类效果还是很不错的