bzoj 1009 GT考试

一道好题，利用kmp维护递推再更新矩阵乘法

这题首先可以递推：

设状态f[i][j]表示长串更新到了i位置，已经匹配短串匹配了j个数

那么我们有转移：

f[i][get_nxt(j)]+=f[i-1][j-1]

当然，你并不懂这是什么意思

我们挨个解释一下

主题思想就是在前面放好的j-1个字符的基础上再放一个字符，看看会发生什么

首先，这里应用的是kmp的next指针的含义（不会kmp的问度娘），我每次新放一个字符是可以枚举出来的，然后我们就看一下放上这个字符之后在放出来的字符串上自己和自己匹配（也就是顺着next数组往上跳），直到跳到一个合法的位置停止，这就是放上新字符后能更新的位置

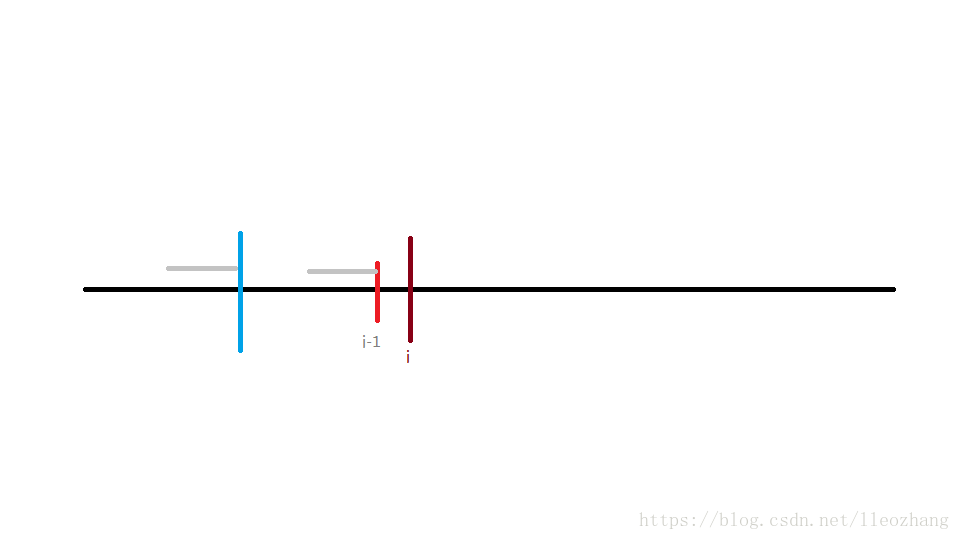
说的可能有点抽象，我们举个例子

如上图，我们根据next数组能够很容易的找出灰色部分是相同的，所以我们比较蓝色和深红色部分是否相同或是否跳到头了即可。

然后转移就很简单了

这样可以得到40分

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
using namespace std;
int dp[1005][1005];
int nxt[1005];
char s[1005];
void get_nxt(int l)
{
    int j=0,k=-1;
    nxt[0]=-1;
    while(j<=l)
    {
        if(s[j]==s[k]||k==-1)
        {
            j++;
            k++;
            nxt[j]=k;
        }else
        {
            k=nxt[k];
        }
    }
}
int get_ans(int posi,int c)
{
    while(posi!=-1&&c!=s[posi]-'0')
    {
        posi=nxt[posi];
    }
    return posi+1;
}
int n,m,w;
map <char,double> M;
int main()
{
        scanf("%d%d%d",&n,&m,&w);
        scanf("%s",s);
        int l=strlen(s);
        get_nxt(l);
        memset(dp,0,sizeof(dp));
        dp[0][0]=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=l;j++)
            {
                for(int k=0;k<=9;k++)
                {
                    int t=get_ans(j-1,k);
                    dp[i][t]+=dp[i-1][j-1];
                    dp[i][t]%=w;
                }
            }
        }
        int ans=0;
        for(int i=0;i<m;i++)
        {
            ans+=dp[n][i];
            ans%=w;
        }
        printf("%d
",ans);
    return 0;
}

但是这还不够，因为这个递推式还可以优化

如何优化？

我们发现，这个转移看似需要用到next数组，但由于每一次调用next数组得到的结果都是一定的，所以我们可以直接把转移方式构造成一个矩阵，然后利用矩阵进行优化即可

AC代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
char s[25];
int nxt[25];
int n,m,k;
struct MAT
{
    int a[25][25];
}zero,ori;
void get_next()
{
    int l=strlen(s);
    int j=0,k=-1;
    nxt[0]=-1;
    while(j<l)
    {
        if(k==-1||s[j]==s[k])
        {
            j++;
            k++;
            nxt[j]=k;
        }else
        {
            k=nxt[k];
        }
    }
}
int get_nxt(int pos,int v)
{
    while(pos!=-1&&s[pos]-'0'!=v)
    {
        pos=nxt[pos];
    }
    return pos+1;
}
MAT mul(MAT &x,MAT &y)
{
    MAT ans=zero;
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<m;j++)
        {
            for(int w=0;w<m;w++)
            {
                ans.a[i][j]+=x.a[i][w]*y.a[w][j]%k;
                ans.a[i][j]%=k;
            }
        }
    }
    return ans;
}
MAT pow_mul(MAT x,int y)
{
    MAT ans=zero;
    for(int i=0;i<=20;i++)
    {
        ans.a[i][i]=1;
    }
    while(y)
    {
        if(y%2)
        {
            ans=mul(ans,x);
        }
        y/=2;
        x=mul(x,x);
    }
    return ans;
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    scanf("%s",s);
    get_next();
    for(int i=1;i<=m;i++)
    {
        for(int j=0;j<=9;j++)
        {
            ori.a[get_nxt(i-1,j)][i-1]++;
        }
    }
    MAT ret=pow_mul(ori,n);
    int ans=0;
    for(int i=0;i<m;i++)
    {
        ans+=ret.a[i][0];
        ans%=k;
    }
    printf("%d
",ans);
    return 0;
}