策略模式

---

策略模式

---

• 策略模式：也叫作政策模式，定义一组算法，将每个算法都封装起来，并且使他们之间可以互换
• 策略模式的使用就是面向对象的继承和多态机制，其通用类图如下：

• • Context封装角色，也叫作上下文角色，屏蔽高层模块对策略、算法的直接访问，封装可能的变化。
  • Istrategy抽象策略角色，策略算法家族的抽象，通常为接口定义每个算法必须具有的方法和属性。
  • ConcreteStrategy具体策略角色，实现抽象策略中的操作该类含有具体的算法。

通用类图的源码如下：

• • public interface IStrategy {
        //定义具体策略必须具有的方法
        public void doSomething();
    }
    
    public class ConcreteStrategy1 implements IStrategy{
        public void doSomething(){
            System.out.println("this is a concreteStrategy");
        }
    }
    
    public class ConcreteStrategy2 implements IStrategy{
    
        @Override
        public void doSomething() {
            // TODO Auto-generated method stub
            System.out.println("This is concreteStrategy2");
        }
    }
    
    public class Context {
        private IStrategy strategy = null;
        public Context(IStrategy strategy){
            this.strategy = strategy;
        }
        public void doSomething(){
            this.strategy.doSomething();
        }
    }
    
    public class Client {
    
        /**
         * @param args
         */
        public static void main(String[] args) {
            // TODO Auto-generated method stub
            Context text = new Context(new ConcreteStrategy2());
            text.doSomething();
            text = new Context(new ConcreteStrategy1());
            text.doSomething();
        }
    }

策略模式的优缺点

• 策略模式的优点
  • 算法可以自由的切换，通过实现抽象策略，通过封装角色对其封装，保证对外提供“可自由切换”的策略。
  • 避免使用多重条件判断，如果有多重策略，那么每个策略只需实现自己的方法，至于采用何种策略，可以通过其他模块决定。
  • 扩展性良好，可以在现有的系统中任意的加入新的策略，只需继承IStrategy接口，符合OCP原则。
• 策略模式的缺点
  • 策略类数量增多，每个策略都是一个类，复用的可能性很小，类数量增多
  • 所有的策略都需要对外暴露，上层模块必须知道有哪些策略，然后才能知道采用哪种策略，可以通过使用工厂方法模式、代理模式和享元模式修正。

策略模式的扩展（工厂方法模式+策略模式）

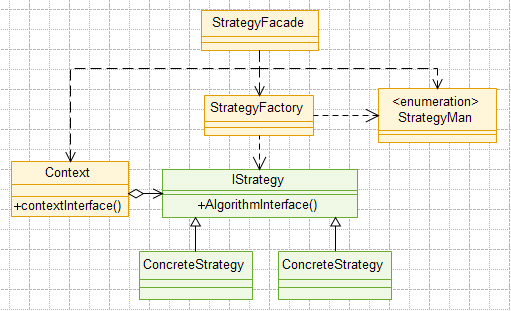
    首先策略枚举StrategyMan，负责对具体策略的映射，然后建立一个简单的工厂，根据策略管理类的枚举项创建一个策略对象，简单而实用，策略模式的缺陷得到了弥补。其通用类图如下：

• public enum StrategyMan {
      Strategy1("com.strategy.ConcreteStrategy1"),
      Strategy2("com.strategy.ConcreteStrategy2");
      String value = "";
      private StrategyMan(String value){
          this.value = value;
      }
      public String getValue(){
          return this.value;
      }
  }
  
  public class StrategyFactory {
      public static IStrategy getStrategy(StrategyMan strategyman){
          IStrategy strategy = null;
          try {
              strategy = (IStrategy) Class.forName(strategyman.getValue()).newInstance();
          } catch (InstantiationException | IllegalAccessException
                  | ClassNotFoundException e) {
              // TODO Auto-generated catch block
              e.printStackTrace();
          }
          return strategy;
      }
  }
  
  public class StrategyFacade {
      public void doSomething(String str){
          StrategyMan sMan = null;
          if(str.equalsIgnoreCase("Strategy1")){
              sMan = StrategyMan.Strategy1;
          }else if(str.equalsIgnoreCase("Strategy2")){
              sMan = StrategyMan.Strategy2;
          }
          IStrategy strategy = StrategyFactory.getStrategy(sMan);
          Context context = new Context(strategy);
          context.doSomething();
      }
  }
  
  public class Client {
  
      /**
       * @param args
       */
      public static void main(String[] args) {
          // TODO Auto-generated method stub
          StrategyFacade sFacade = new StrategyFacade();
          sFacade.doSomething("Strategy1");
      }
  }