LeetCode 287. Find the Duplicate Number （python 判断环，时间复杂度O（n））

LeetCode 287. Find the Duplicate Number

暴力解法

时间 O（nlog(n)），空间O（n），按题目中Note“只用O（1）的空间”，照理是过不了的，但是可能判题并没有卡空间复杂度，所以也能AC。

class Solution:
    # 基本思路为，将第一次出现的数字
    def findDuplicate(self, nums: List[int]) -> int:
        s = set()
        for i in nums:
            a = i in s
            if a == True:
                return i
            else:
                s.add(i)

双指针判断环

时间O（n），空间O（1），思路十分巧妙，但是使用条件比较苛刻。根据题目给出的条件，恰好能用这种解法，这应该也是出题人推荐的解法。

题意分析：

1. 输入的序列有n+1个数字，每个数字在1~n之间取，这为构成数字环创造了条件。
2. 只有一个数字有重复，所以只可能构成一个环。

注:上面所说的环是指1->2->3->1

以样例1为例：[1,3,4,2,2]

0	1	2	3	4
1	3	4	2	2

如下图所示，其中2->4->2构成环，入环点为2

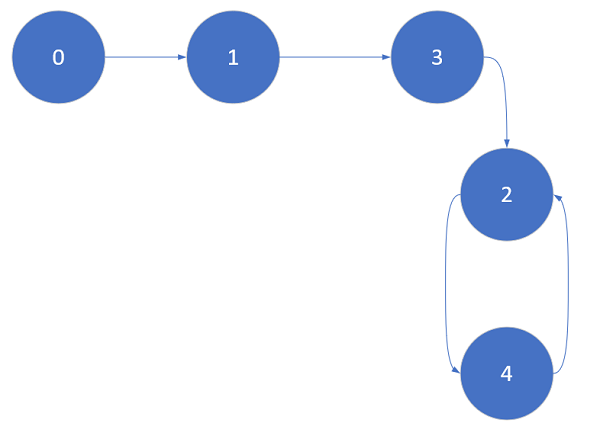
解题思路

由题意分析可知，每个样例都可以画成这样一张图，我们只需要找出图中的环，并找出入环点，即为所求的重复数字key，下面都用key表示所求的重复数字。

为什么必定存在环

以样例1为例，图中出现了5个点0-4，图中存在5根指针线，5个点5根线，必定存在环。
n个点，点的范围去0~n-1，n根线，必定存在环。（n-1根线是恰好无环的情况，自己画图可知）

找环的方法

设置一个慢指针slow，一个快指针fast。slow每次走一步，fast每次走两步，如果slow与fast能相遇，说明图中存在环，并且相遇点一定存在于环中。

为什么key一定为入环点？

有题意分析中的表可知，key的入度一定大于1，即不止一个点可以直接到key。而key一定存在于环中，所以key一定为入环点。样例1中3,4都可到达2，2的入度2，2为入环点，即为所求的key。

怎么找入环点key?

slow和fast相交的点记为相遇点P。
slow和fast从起点0到相遇点P运行步骤如下：

这个相遇点P与起点0到达入环点key的步数 差距为环L的整数倍，故设置slow2从起点0开始，每次走一步，slow从相遇点P开始，每次走一步，slow和slow2一定会相遇在入环点key。

我们可以有一个小小的证明，如下图

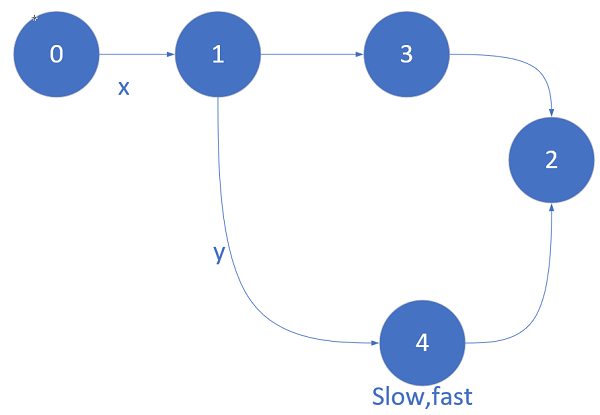
设起点0到达入环点key的步数为x，相遇点P到达入环点key的步数为y。
设slow指针走到相遇点P的步数为t，fast走到相遇点P的步数为2*t。
设走完环一圈的步数为L

2 * t - x + y = M * L（一）
t - x + y = N * L （二）
fast指针在环中走的步数2t-x，此时到达相遇点P，key->P->key步数为2t-x+y = M * L，正好为L的M倍，M为常数。（一）式
slow指针在环中走的步数t-x，此时到达相遇点P，key->P->key步数为t-x+y = N * L，正好为L的N倍，N为常数。（二）式

2倍（二）式 减 （一）式
y-x = （2N-M） * L
所以y与x的步数差距为L倍的环。
得证。

如何确定起点0一定会进入包含key的环？

假设存在不包含key的环，起点0在不包含key的环中绕圈。

0	a1	a2	a3	a4	a5	a6
b1	b2	b3	b4	b5	b6	b7

按题意不包含环，b[i]与b[j]一定不相等（i != j）
由于b1~b7从1开始，所以b[i]只能从a[j]中取（1<=i<=7，1<=j<=6）
从6个数字的集合a中取7个数字，所以假设不成立，必定存在相同数字b[k]，即为key。

代码如下

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        # 如果只有两个元素，第一个元素一定是重复元素
        if len(nums) == 2:
            return nums[0]
        
        # fast每次走两步，slow每次走一步，起始点可以为任意位置
        fast = 0
        slow = 0
        # python没有do while，所以在循环外写了一遍
        slow = nums[slow]
        fast = nums[nums[fast]]
        while slow != fast:
            slow = nums[slow]
            fast = nums[nums[fast]]
        
        # fast从起点每次走一步，一定会与slow相遇，此时slow可能在环中走了多倍的L步。
        # L为环一圈的步数
        fast = 0
        while fast != slow:
            slow = nums[slow]
            fast = nums[fast]
        return fast