这几天终于认真搞懂了线段树,就赶紧生产了篇学习笔记来热热知识。(我真的好菜啊)
线段树呢,是一种很有用的数据结构(点头),对于一些区间查询、修改都能方便实现,还有好多好多的奇异功能(哇),也是学习一些高级du liu数据结构的基础,对于一名OIer还是 有认真学习的必要的。
线段树是一种二叉搜索树,什么叫做二叉搜索树,首先满足二叉树,每个结点度小于等于二,即每个结点最多有两颗子树,何为搜索,我们要知道,线段树的每个结点都存储了一个区间,也可以理解成一个线段,而搜索,就是在这些线段上进行搜索操作得到你想要的答案。
我们先来看看这么一个栗子:
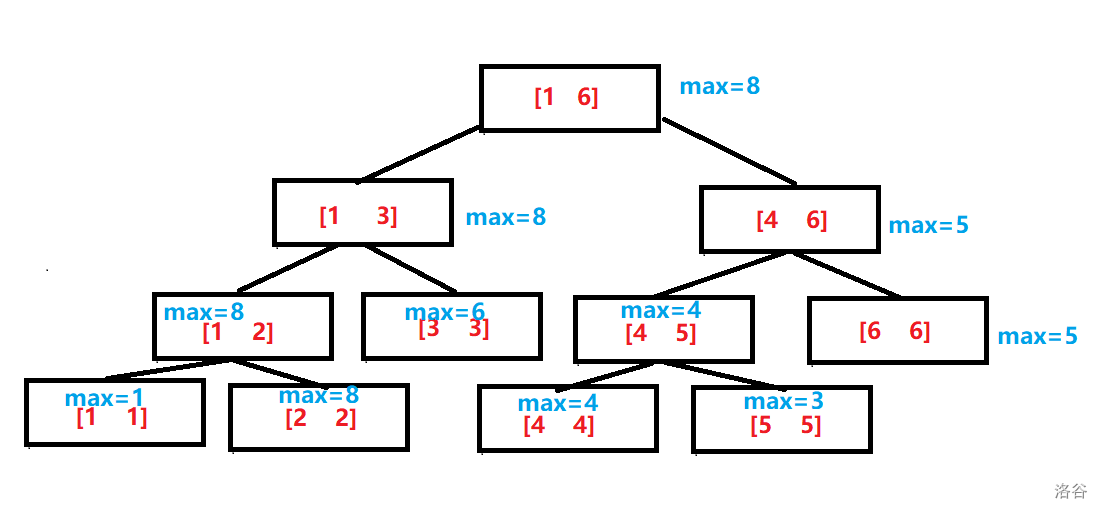
这是一个比较简单的求区间最大值的线段树。每个节点红色部分是这个节点所维护的区间,蓝色部分是这个区间里的最大值,并且每个叶子结点的值就是原数组的值。
所以我们可以发现,每个非叶子结点的度都为二,且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。
明白了上面这个道理,我们接下来就捋一捋每个节点如何来储存区间,还有如何快速找到非根节点的父亲和非叶子节点的儿子。
对于线段树的储值,我们一般不会去记录l和r的值,看一下上面的图,我们可以发现,根节点记录的是整个数组的最大值,它的两个儿子分别记录的是 1--3 和 4--6 的值,仔细看,你是不是想到什么?
没错,就是二分。当根节点记录的是 1--n 的值时,它的左儿子就记录的是区间 1--(1+n)/2 的值,右儿子就记录的是区间 (1+n)/2+1--n 的值,以此类推,根节点的左右儿子也是如此,就这样分到 l=r ,此时就是叶子节点了,也就可以将其赋值。
赋值之后呢,我们现在只给叶子节点赋值而已,那其他的节点呢?
所以,我们通常使用 递归 来实现整棵树的修改,只要不断地递归左右子树,直到 l=r 停止,返回的时候顺便进行修改即可。
好的,到这里,如果你捋清楚了如何进行整棵树的修改,那么我们接下来就来琢磨琢磨如何来给每个节点标一下下标。
下标可是很重要的。
对于上述线段树,我们增加绿色数字为每个结点的下标。
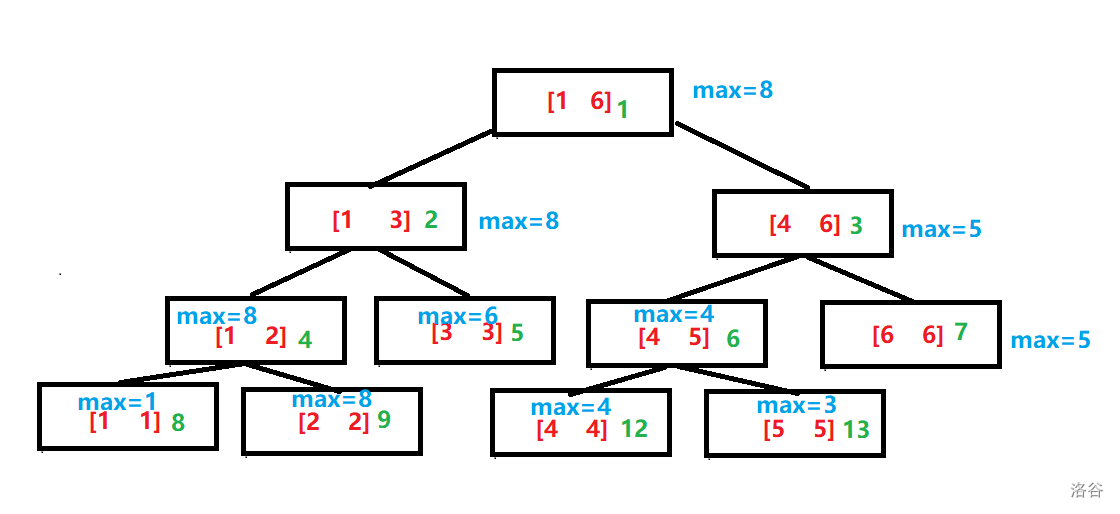
“ 1、2、3、4、5、6、7、8、9、12?!! ”
“ 怎么直接从 9 跳到了 12 ? ”
“ 噢!原来中间其实是有两个空间的呀! ”
虽然没有用到,但是一定要开,因为你不会知道这 5 这个节点到底是不是叶子节点,所以以防万一。这也是无优化线段树的缺点,空间好大,常M别怕
一般没有优化过的线段树,是需要 (2 * 2^{k} ( 2^{k-1} < n < 2^k)) 个空间的,所以一般会开到 4×n 的空间防止RE。
仔细观察上图,我们应该不难发现,左儿子的下标是父亲下标的两倍,而右儿子的下标就是左儿子的再加上1。
总结一下:
-
l = x × 2
-
r = x × 2 + 1
(x是父亲的下标,l是左儿子的下标,r是右儿子的下标)
具体证明也不太难,请大佬自行百度,这里不做细讲
一般,我们常用位运算来计算:
-
l = x << 1
-
r = x << 1 | 1
好了,讲了那么久,终于能开心地打一打代码了!
#define ls (x<<1)
#define rs (x<<1|1)
#define mid (l+r>>1)
#define MAXN 50010
int a[MAXN],t[MAXN<<2]; //a为原来区间,t为线段树
void pushup(int x) //更新函数,这里是实现最大值,同理可以变成最小值,区间和等
{
t[x]=max(t[ls],t[rs]);
}
//递归方式建树 build(1,n,1);
void build(int l,int r,int x) //l表示当前区间的左端点,r表示当前区间的右端点,x表示当前结点的下标
{
if(l==r) //左端点等于右端点,即为叶子节点,直接赋值即可
{
t[x]=a[l];
return ;
}
build(l,mid,ls); //递归构造左儿子结点
buile(mid+1,r,rs); //递归构造右儿子结点
//这里的mid是l和r的中点,目的是为了将l--r分为两个区间
pushup(x); //更新操作
}
下面我们就来讲一下区间的查询修改和单点的修改。
区间修改,顾名思义,对某个区间的值进行更新。那么要如何更新呢,可以想一想,其实和建树是差不多的(点头)
(Three minutes later~)
好,其实我们可以发现,上面的建树,换个说法,就是对整个区间的更新,那么为了可以实现其中一部分区间的更新,我们需要在上面的建树代码中,当前节点往下跑的方向给一些限制。
举个例子,我们要将 [ 3 , 5 ] 这个区间的每一个值改为5,如下图。

其实我们可以发现,每次对于向下跑的方向,我们可以根据现在左右儿子管理的区间,里面有没有包含要修改的区间,有的话就可以朝着那个方向继续跑下去。
刚刚在 build 函数里面,有这么两个变量—> l和r,这两个变量的意思就是当前节点管理的区间范围,我们可以将最左(l)和最右(r)分别与要修改区间的左和右作比较就行了,到最后一定会跑到一个要修改的点上。
口胡大师当然是不行的,所以现在我们来动手操作一下:
#define ls (x<<1)
#define rs (x<<1|1)
#define mid (l+r>>1)
#define MAXN 50010
int a[MAXN],t[MAXN<<2];
void pushup(int x){t[x]=max(t[ls],t[rs]);}
//同样用递归的方式修改区间
void updata(int L,int R,int v,int l,int r,int x)
//L,R表示修改区间的左右端点,v表示要修改的数值
//l,r,x的含义见build
{
if(l==r)
{
t[x]=v;//将第x个数修改为v
return ;
}
if(L<=mid)
//左儿子管理的区间有包括部分要修改的区间
updata(L,R,l,mid,ls(x));
if(R>mid)
//右儿子管理的区间有包括部分要修改的区间
updata(L,R,mid+1,r,rs(x));
pushup(x);
}
如果还不太懂的话,可以自己画图模拟一下(汗)。
然后对于单点修改,其实也是差不多的。因为修改的只有一个点,所以,对于当前非叶子结点,如果左儿子管理的区间没有包括这个节点的话,就一定在右儿子那边。
(丢你代码(大雾
void updata(int i,int v,int l,int r,int x)
//i表示要修改的节点
{
if(l==r)
{
t[x]=v;//将第x个数修改为v
return ;
}
if(i<=mid)
updata(i,v,l,mid,ls);
else
updata(i,v,mid+1,r,rs);
pushup(x);
}
好的,现在我们已经完成了单点/区间修改,如果你已经完全理解了,那么对于接下来区间查询就不会太难理解了。
(单点修改的话直接找a数组查询,记得在修改的时候带上a数组qwq)
(话说哪个出题人那么无聊出单点修改)(大雾)
对于区间查询,其实和区间修改差不多,至少精髓是一样的(话说这不废话吗)
假如我们要查询 [ 2 , 5 ] 的最大值,就像下面这样
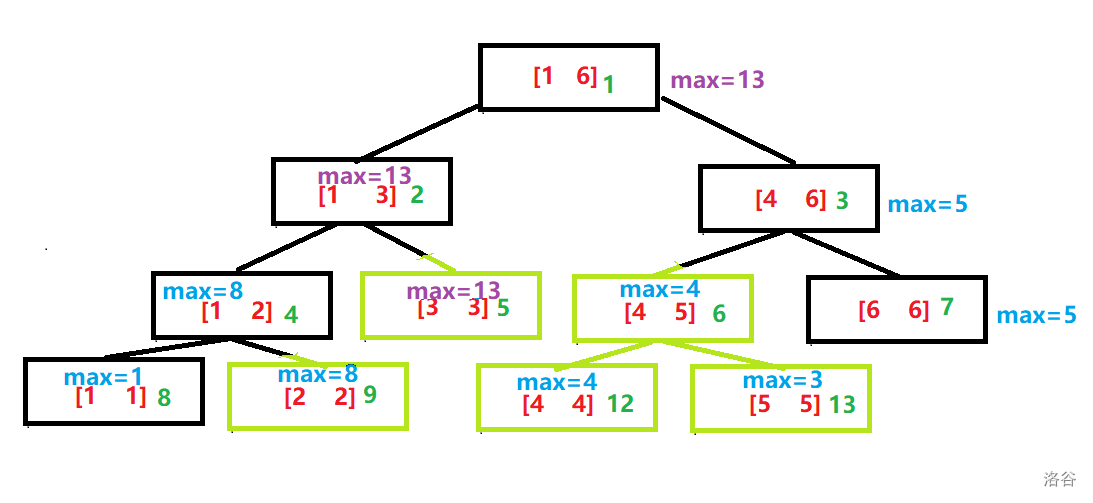
仔细瞧,说是一共要查询2、3、4、5这四个节点,其实我们只要查询 [ 2 , 2 ] 、 [ 3 , 3 ] 、[ 4 , 5 ] 这三个区间的最值,然后再来进行比较,就可以缩短一部分查询的时间,对于大数据的话就不止一点了(排开某些毒瘤数据、最坏情况),所以这也是线段树的其中一处优越。
大家要先把思路捋明了,代码也就清晰了(温馨提示(大雾
int query(int L,int R,int l,int r,int x)
//几个变量含义和updata的一样qwq
{
if(L<=l&&r<=R) return t[x];
//如果要查询的区间包括当前的区间,就直接返回当前区间的最大值
ll ans=-19260817;
//一般这里用long long,以防万一
if(L<=mid)
ans=max(ans,query(L,R,l,mid,ls));
if(R>mid)
ans=max(ans,query(L,R,mid+1,r,rs));
//此处两个if和updata的用意一样
return ans;
}
读到这,恭喜你,你已经掌握了最基本的线段树了(大佬orz)
然后你就迫不及待地去切题了。
嗯?模板?你怒打了一棵线段树,交了上去。
qwq

什么呀,怎么还有3个黑色的东西(大雾),然后你就仔细地调自己代码,看看有哪里写的不一样。
其实,线段树对于查询修改的复杂度都是 O(logN) , 但是上文提过,有些毒瘤出题人,弄了些最坏情况,把线段树的查询修改卡到 O(NlogN) (比如让你对所有区间进行修改),那么现在的话就比暴力还慢了,所以聪明的人们发明了 lazy_tag (懒标记),顾名思义,就是在更新区间的时候偷懒,如何偷懒呢,且听我一一道来。
通过上面对区间修改的讲解,我们可以发现,每次修改的时候总是要跑到叶子节点后才来进行修改,然而这样会比直接暴力扫区间还慢。我们是不是可以不用跑到叶子节点来修改区间呢?
当我们从根节点往下跑的时候,如果这个非叶子节点管理的区间包含在修改区间的范围内时,我们可以直接对这个节点进行修改,然后开一个数组标记修改的值,这个数组称为lazy数组,我们已经将这部分区间修改,接着就可以直接返回了。
如果当我们需要更下面的节点怎么办?我们只修改了下面节点的父节点,并没有将下面的节点更新。此时我们刚刚开的那个lazy数组就起作用了。
我们可以利用父节点的lazy值,来修改子节点的值,然后将子节点的lazy值改为父节点的lazy值,接着把父节点的lazy值清零就行了。
(说白了就是将lazy下传)
好了,如果现在已经理解lazy_tag的作用和实现方法的话,就来coding一下qwq
(这里我们以刚才的模板为例子qwq)
void pushdown(ll i,ll k)//将lazy值下传
//i表示当前节点,k表示i节点管理区间长度
{
if(lazy[i])//如果有lazy值的话
{
lazy[ls(i)]+=lazy[i];
lazy[rs(i)]+=lazy[i];
//将lazy值赋给左右子节点
t[ls(i)]+=(k-(k>>1))*lazy[i];
//因为左子节点里面有(k-k/2)个叶子节点,每个叶子节点都要加上lazy值
t[rs(i)]+=(k>>1)*lazy[i];
//同上
lazy[i]=0;
//修改完之后就要把lazy值归0,否则会重复计算
}
}
因为这是在修改是的lazy,所以updata也要相对应进行修改。
void updata(int L,int R,int v,int l,int r,int x)
//L,R表示修改区间的左右端点,v表示要修改的数值
{
if(L<=l&&r<=R)//如果要修改的区间包含当前区间
{
lazy[i]+=v;
t[i]+=v*(r-l+1);
//思路和pushdown一样
return ;
}
pushdown(x,r-l+1);//因为下面的节点可能之前没有修改过,所以我们要pushdown一下
if(L<=mid)
//左儿子管理的区间有包括部分要修改的区间
updata(L,R,v,l,mid,ls(x));
if(R>mid)
//右儿子管理的区间有包括部分要修改的区间
updata(L,R,v,,mid+1,r,rs(x));
pushup(x);
}
同样的,query也要进行相对应的修改
int query(int L,int R,int l,int r,int x)
{
if(L<=l&&r<=R) return t[x];
pushdown(x,r-l+1);//和updata同样,查询之前先更新
ll ans=-19260817;
if(L<=mid)
ans=max(ans,query(L,R,l,mid,ls));
if(R>mid)
ans=max(ans,query(L,R,mid+1,r,rs));
return ans;
}
恭喜你,到这里你就已经掌握一个线段树的基本写法了,现在你就可以开心切题了!
线段树只是一种较基础的数据结构,对于一些关于线段树的 高级算法,等以后有时间再讲吧qwq(
写在最后:
害,这次的文章咕了好久,咕了差不多大半年的时间了(sta-> 3-29 / fin-> 8-02),剩下的lazy_tag还是在jzsc的闲余时间完善的,才发现我差不多都完干净了qwq。其实我写这篇博客主要是为了给以后自己复习用 (翻译:我太菜了),如果说,这篇博客可以帮助到想学线段树的大佬的话,我是非常高兴的,我将一些较难懂的点给简单化详细化 (话说好像没什么难懂的点(大雾 ),所以对于像我一样的蒟蒻还是挺容易理解的qwq