哦末,刚学了费用流,就来造福人民,哈哈,大佬勿喷(其实是GDOI爆零,心情不好写一篇博客安慰自己)
好了,回归正题,这里我只讲费用流的两种方法(没有负权环)
一样的,建反向边,然后就开始操作了!
首先,是MCMF费用流,即连续用SPFA计算从起点到终点的最小费用,在进行SPFA中顺带记录流量、前一个点、前一条边,然后,就。。。从终点回去更新一路到起点就行了,先给出SPFA(为什么会对?找最短费用,然后还有反向边后悔,为什么不行?):
memset(v,false,sizeof(v));v[st]=true;/*统计这个数是否在队列*/
head=1;tail=2;list[1]=st;/*从前点开始*/
memset(dis,63,sizeof(dis));dis[st]=0;/*最小费用,从起点开始*/
b[ed]=-1;/*还要判断是否可行,b代表的前一条边,不太理解看后面*/
while(head!=tail)
{
int x=list[head];
for(int k=last[x];k;k=a[k].next)/*边目录存*/
{
int y=a[k].y;
if(a[k].c>0 && dis[x]+a[k].k<dis[y])/*看看这条可行边是否可以更新y点*/
{
dis[y]=dis[x]+a[k].k;/*更新*/
flow[y]=mymin(a[k].c,flow[x]);/*更新最多能到达的流量*/
qian[y]=x;/*更新到达y点的点*/b[y]=k;/*同时更新边*/
if(v[y]==false)/*扔进队列*/
{
v[y]=true;
list[tail++]=y;
if(tail==n+1)tail=1;
}
}
}
head++;
if(head==n+1)head=1;
v[x]=false;/*找完后将他改为false*/
}下面给出将边修改的过程:
if(b[ed]!=-1)/*存在流时进来*/
{
int y=ed,root=0;/*更新边流量的过程*/
while(y!=st)
{
root=b[y];y=qian[y];/*找出这条最小费用路径的边和点*/
a[root].c-=flow[ed];
a[a[root].other].c+=flow[ed];/*边处理*/
}
zans+=flow[ed];
cost+=flow[ed]*dis[ed];/*更新花费与流量*/
}
return b[ed]!=-1;//返回bool值 然后,吗。。。再来个主函数(感觉好鸡肋得主函数):
int main()
{
scanf("%d%d",&n,&m);
st=1;ed=n;
for(register int i=1;i<=m;i++)
{
int x,y;
ll z,k;
scanf("%d%d%lld%lld",&x,&y,&z,&k);
ins(x,y,z,k);
}
flow[st]=ll(999999999999999);/*初始化起点有无数的流量*/
while(spfa()==true);//一直到不存在路径为止。
printf("%lld %lld",zans,cost);/*输出*/
return 0;
}ZKW大佬优化后的ZKW牌费用流(祛风除湿止痛费用流哟,年轻人):
大佬的方法就是找到多条增广路,用SPFA找到多条增广路(从终点开始计算(然而从起点开始好像也无所谓啦!但是,作者用自己的亲身试验证明,会慢!╯﹏╰,不知为什么))。
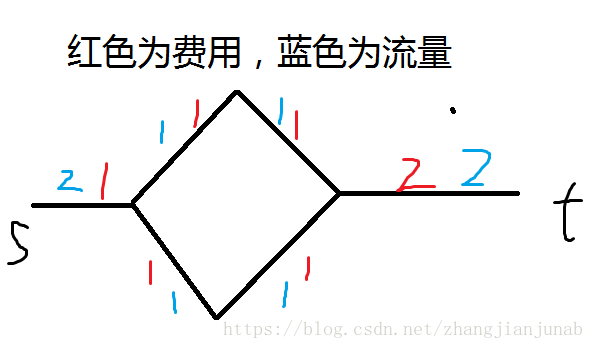
如图:
这张图,明显用MCMF要两次SPFA,但是,SPFA的特点是可以计算出所有点离起点有多远!所以,咱们可以用一次递归来找出所有最短路径。
ZKW费用流的SPFA
int list[1100],head,tail;/*队列*/
inline bool spfa()
{
memset(v,false,sizeof(v));v[ed]=true;/*判断是否进入队列*/
memset(d,-1,sizeof(d));d[ed]=0;/*从终点到这里要多少费用*/
head=1;tail=2;list[head]=ed;/*从终点出发*/
while(head!=tail)
{
int x=list[head];
for(int k=last[x];k;k=a[k].next)
{
if(a[a[k].other].c>0/*由于是倒着搜的,所以边也要反向边*/ && (a[a[k].other].k+d[x]<d[a[k].y] || d[a[k].y]==-1))/*判断边是否可行并更新*/
{
d[a[k].y]=a[a[k].other].k+d[x];/*更新*/
int y=a[k].y;
if(v[y]==false)
{
v[y]=true;
list[tail]=y;
tail++;
if(tail==n+1)tail=1;/*这里可以用SLF优化*/
}
}
}
head++;
if(head==n+1)head=1;
v[x]=false;
}
return d[st]!=-1;/*返回bool值*/
}inline ll mymin(ll x,ll y){return x<y?x:y;}/*找最小值*/
long long find(int x,ll f)
{
v[x]=true;
if(x==ed)return f;
ll ans=0,t=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(v[y]==false/*这个点在这条路径没走过才可以走,否则。。。Balabala*/ && a[k].c>0 && d[x]-a[k].k==d[y]/*类似分层的操作*/ && ans<f)
{
ans+=t=find(y,mymin(a[k].c,f-ans));/*是不是很眼熟?*/
a[k].c-=t;a[a[k].other].c+=t;cost+=t*a[k].k;
}
}
return ans;/*妥妥的像最大流*/
}牛逼的!主函数:
int main()
{
scanf("%d%d",&n,&m);
st=1;ed=n;
for(int i=1;i<=m;i++)
{
int x,y;
ll z,l;
scanf("%d%d%lld%lld",&x,&y,&z,&l);
ins(x,y,z,l);
}
ll zans=0;
while(spfa()==true)/*建图完成!*/
{
do
{
memset(v,false,sizeof(v));
zans+=find(st,ll(999999999999999));/*多次查找,找出所有增光路哦*/
}while(v[ed]==true);/*走不到终点,退出!*/
}
printf("%lld %lld",zans,cost);
return 0;
}然而。。。
还可以更优!
细心的同学可以发现了一个尴尬的情况:
但是:
于是,当找到t>0时,break;就可以了!
inline ll mymin(ll x,ll y){return x<y?x:y;}
long long find(int x,ll f)
{
v[x]=true;
if(x==ed)return f;
ll ans=0,t=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(v[y]==false && a[k].c>0 && d[x]-a[k].k==d[y] && ans<f)
{
ans+=t=find(y,mymin(a[k].c,f-ans));
a[k].c-=t;a[a[k].other].c+=t;cost+=t*a[k].k;
if(t!=0)break;
}
}
return ans;
}但是,你又会发现,不断的break,多次递归,太慢了。
于是,你可以将递归加个回溯,这就快多了:
find函数:
inline ll mymin(ll x,ll y){return x<y?x:y;}/*找最小值*/
long long find(int x,ll f)
{
v[x]=true;
if(x==ed){v[x]=false;return f;}
ll ans=0,t=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(v[y]==false/*这个点没走过才可以走,否则更新边的流量是会Balabala*/ && a[k].c>0 && d[x]-a[k].k==d[y]/*类似分层的操作*/ && ans<f)
{
ans+=t=find(y,mymin(a[k].c,f-ans));/*是不是很眼熟?*/
a[k].c-=t;a[a[k].other].c+=t;cost+=t*a[k].k;
}
}
v[x]=false;/*回溯*/
return ans;/*妥妥的像最大流*/
}
主函数:
int main()
{
scanf("%d%d",&n,&m);
st=1;ed=n;
for(int i=1;i<=m;i++)
{
int x,y;
ll z,l;
scanf("%d%d%lld%lld",&x,&y,&z,&l);
ins(x,y,z,l);
}
ll zans=0;
while(spfa()==true)/*建图完成!*/
{
zans+=find(st,ll(999999999999999));/*开心,一次就够!*/
}
printf("%lld %lld",zans,cost);
return 0;
}
最后,贴上整个代码,祝大家学会网络流:
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
struct node
{
int y,next,other;
ll c,k;
}a[201000];int last[1000],len;
long long d[1100];
bool v[1100];
int n,m,st,ed;
ll cost=0;
inline void ins(int x,int y,ll c,ll k)
{
len++;
a[len].y=y;a[len].c=c;a[len].k=k;
a[len].next=last[x];last[x]=len;
len++;
a[len].y=x;a[len].c=0;a[len].k=-k;
a[len].next=last[y];last[y]=len;
a[len-1].other=len;
a[len].other=len-1;
}
int list[1100],head,tail;/*队列*/
inline bool spfa()
{
memset(v,false,sizeof(v));v[ed]=true;/*判断是否进入队列*/
memset(d,-1,sizeof(d));d[ed]=0;/*从终点到这里要多少费用*/
head=1;tail=2;list[head]=ed;/*从终点出发*/
while(head!=tail)
{
int x=list[head];
for(int k=last[x];k;k=a[k].next)
{
if(a[a[k].other].c>0/*由于是倒着搜的,所以边也要反向边*/ && (a[a[k].other].k+d[x]<d[a[k].y] || d[a[k].y]==-1))/*判断边是否可行并更新*/
{
d[a[k].y]=a[a[k].other].k+d[x];/*更新*/
int y=a[k].y;
if(v[y]==false)
{
v[y]=true;
list[tail]=y;
tail++;
if(tail==n+1)tail=1;
}
}
}
head++;
if(head==n+1)head=1;
v[x]=false;
}
return d[st]!=-1;/*返回bool值*/
}
inline ll mymin(ll x,ll y){return x<y?x:y;}/*找最小值*/
long long find(int x,ll f)
{
v[x]=true;
if(x==ed){v[x]=false;return f;}
ll ans=0,t=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(v[y]==false/*这个点没走过才可以走,否则更新边的流量是会Balabala*/ && a[k].c>0 && d[x]-a[k].k==d[y]/*类似分层的操作*/ && ans<f)
{
ans+=t=find(y,mymin(a[k].c,f-ans));/*是不是很眼熟?*/
a[k].c-=t;a[a[k].other].c+=t;cost+=t*a[k].k;
}
}
v[x]=false;
return ans;/*妥妥的像最大流*/
}
int main()
{
scanf("%d%d",&n,&m);
st=1;ed=n;
for(int i=1;i<=m;i++)
{
int x,y;
ll z,l;
scanf("%d%d%lld%lld",&x,&y,&z,&l);
ins(x,y,z,l);
}
ll zans=0;
while(spfa()==true)/*建图完成!*/
{
zans+=find(st,ll(999999999999999));/*多次查找,找出所有增光路哦*/
}
printf("%lld %lld",zans,cost);
return 0;
}最后,总结一下,稀疏图用MCMF会快(很暴力,我喜欢!),稠密图还是用ZKW费用流吧(多条的增光路哟,年轻人!)
update:
1. 倒着跑是优化,因为终点到起点是一条路,但是如果是起点出发,会有一些更短的但不是去向终点的路径
(大佬表示:垃圾,没证明)(萌新表示:垃圾,看不懂!)(我:但是我可以秀图!)
注:上面的图片侵权抱歉!