关于半平面交的探讨

目录

• 参考文献
• 题目
• 求法
  • 约定
  • 如何求一个点是否在其半平面
  • 简略求法
  • 对于栈中元素更加形象的存储和讲解方式
  • 环的出现及处理
  • 无交情况判断
    • 无限交
    • 无交的情况
    • 平行的情况
    • 解集为点或者线段
    • 代码
    • 另外一种双端队列的写法
      • 讲解
      • 代码会出的问题
    • 在线做法的idea
• 题目代码
• 一道练手题
• 小结

参考文献

你谷日报真的是太好啦：

主要讲解：https://www.luogu.com.cn/blog/105254/dui-ban-ping-mian-jiao-suan-fa-zheng-que-xing-xie-shi-di-tan-suo

半平面交中双端队列的一种错误写法的讲解：https://www.luogu.com.cn/blog/wjyyy/geometry1

本文会有许多99%和本文相似的地方，因为就是从这个日报才终于看懂了半平面交，对于半平面交的理解才开始加深。

除小部分代码其余皆采用此博客的代码，图片也大部分是基本上只要是好看的都是，好像只要看水印就行了。

我以前的证明都是什么垃圾啊，严谨又不严谨，就是一坨*

当然，本文的证明还是更加的偏感性，因为计算几何理性证明是在太难了QAQ，为什么我不会理性的计算几何啊(╯‵□′)╯︵┻━┻。

题目

【题意】
在一个有限大（-10 0000<=x,y<=10 0000)的平面坐标系上有n个半平面（注意有限的），每个半平面给出一条有向线段（x1,y1)——>(x2,y2）。
每个半平面的有效区域都是左侧（包括此直线）。求这n个半平面的交的面积。
【输入文件】
第一行一个整数n（1 <= n <= 2 0000）
下来n个半平面。每个半平面一行四个整数x1,y1,x2,y2。（-100000 <= x1,y1,x2,y2 <= 100000)
【输出文件】
一行，输出n个半平面的交的面积（保留一位小数），如果有效面积不存在则输出"0.0"。
【样例1输入】
3
1 1  9 9
5 10  4 10
0 3 0 2
【样例1输出】
50.0

【样例2输入】
4
0 0  10 0
10 0  10 10
10 10 0 10
11 11 11 0
【样例2输出】
0.0

半平面交中的直线更像是有向直线，你可以理解为把向量扩展到了直线。

而有向直线的极角则为向量的幅角。

考虑(ax+by+c≥0)，首先有(ax+by+c=0)，如果(a>0)，那么(x'=x+k(k≥0))都满足此要求，此时解集是在这条直线的右边，如果(a<0)是在左边，(a=0)则要看(b)，此时就是上下之分了，因此，有一条直线的半平面更多的是这个直线的一个二元一次不等式的体现，而其解集就是其的半平面，这里默认半平面包括这条直线。

但是，这里却说是有向直线的左边，有向直线和直线不同，多了方向，因此其左右边更多的清晰，即把这个平面旋转，旋转到直线与转前的(y)轴平行，且方向为旋转前的(y)轴正半轴的方向，左右边就是指这个时候的左右边。（简单而言就是以这条直线自己的视角看的左右边）

因此，(x+y≥0)和(-x-y≥0)是同一条直线，但是方向却不同，至于如何把二元一次不等式转换成有向直线，下面的练习会讲，这里先不讲。

半平面交求的是多条直线的半平面的重合部分，也就是多个二元一次方程的解集。

这里讲的无交情况总共有两种，一种是解集为空，一种是解集无限。（当然，大部分的题目都会让你在一个有限的正方形或者有限的范围跑半平面交，下文会大概的提一提这种情况如何处理，但是呢，其不是主要无交情况，代码中主要也不会考虑到这种情况，请大家阅读时发现无限交没有提到也不要吃惊，至于如何限定在一个范围？如果限定在一个正方形，就把正方形的四条边以有向直线的方式加入到半平面交即可，其余类似）

当然，因为有向线段的左边更加直观，所以一般在求解的过程中都是保存代表有向直线的向量，而且这能更好的利用叉积。

求法

约定

以下来自https://www.luogu.com.cn/blog/105254/dui-ban-ping-mian-jiao-suan-fa-zheng-que-xing-xie-shi-di-tan-suo。

代码约定：

typedef pair<int, int> pad;/*pad awa*/

const double pi =acos(-1), eps =1e-6;

/*点或者说向量*/
struct vect{
    double x, y;
    vect(){}
    vect(double xx, double yy):x(xx), y(yy){}
    vect operator + (vect v){ return vect(x+v.x, y+v.y); }
    vect operator - (vect v){ return vect(x-v.x, y-v.y); }
    vect operator * (double mu){ return vect(mu*x, mu*y); }
    double operator / (vect v){ return x*v.y-y*v.x; }/*叉积*/
};

/*直线*/
struct line{
    vect u, v;
    double angle;
    line(){}
    line(vect uu, vect vv):u(uu), v(vv){ angle =atan2(vv.y-uu.y, vv.x-uu.x); }
};

line hull[];/*储存 凸包 / 环（定义见下） / 答案*/

line ls[];/*代表加入直线序列*/

int l, r;/*左右指针，左闭右开*/

/*(a > b)*/
inline bool gtr(double a, double b){ return (a-b > eps); }

/*(a == b)*/
inline bool eq(double a, double b){ return (a-b < eps && a-b > -eps); }

/*点是否在有向直线右侧，是返回 true，否（在左侧或直线上）返回 false*/
inline bool onright(line f, vect w){ return (gtr((w-f.u)/(f.v-f.u), 0)); }

/*求两条直线交点（无交情况未定义）*/
vect getIntersection(line f, line g){
    double w =((g.u-f.u)/(f.u-f.v))/((f.u-f.v)/(g.u-g.v));
    return g.u+(g.u-g.v)*w;
}

/*用于排序的比较函数*/
int cmp(line A, line B){
    if(eq(A.angle, B.angle)) return onright(B, A.u);/*有向直线最左的会排在最后面，并被保留*/
    else return (gtr(B.angle, A.angle));
}

说明：

1. 文中的半平面交默认是有向直线左侧交，包括边界。
2. 实现中所用的计较都是直接使用 atan2 的返回值，并未做其他处理（因此值域为 ((−π,π])）、
3. 这里的增量法实现都是按直线极角从小到大加入的。
4. 话说下面以及上面提到的 "增量法"、"标准双端队列做法"，一种典型示范就是刘汝佳书中有关半平面交章节的示例代码。或者关于这种做法的实现细节及说明，可以先看看之前的 计算几何日报。当然，本文的代码来自此篇日报

如何求一个点是否在其半平面

额，其实你会发现一个事情，对于有向直线(a->b)，存在点(c)在其半平面，那么(vec{ab}*vec{ac}≥0)，这是判断是否在半平面的充要条件，当然，上面约定函数中看是否在直线右边也是同样的原理。

简略求法

现在，我们考虑把所有的直线按照极角排序，什么？你问我极角怎么求？已知有向直线(AB)，其极角为(atan2(y_B-y_A,x_B-x_A))。

其实基本上很多也就半平面交和凸包好吧几何题都可以用极角排序的方式确定遍历直线的顺序，设排序后的数组为(a)数组。

不妨先讲个粗略的求法，最后一步步弥补缺漏，最后完成代码。

因为面积有限，不难先猜想其是个多个多边形，后面发现不能是非凸多边形（自己画一个就知道了），于是又发现其必须只能是一个（自己画以下），所以其是一个凸包（这也就可以解释为什么前面要用极角排序了，为了方便下文求凸包）。

我们先讲个类似凸包的做法，看看大家有没有异议，用栈（栈用(A)代表）保存与半平面交部分有直接接触的有向直线（也就是构成半平面交轮廓的直线），对于前两条直线，直接储存（红色半平面和蓝色半平面）。

现在已经有了(top)条直线，对于第(i)（这里(i=3)）条有向直线（绿色半平面）

如果(A_{top})和(A_{top-1})的交点在(a_i)的半平面，那么说明直接插入即可，如果刚好在直线上也是一样，如果不在，那么说明什么，如图，你会发现蓝色半平面的有向（这里根本看不出有向好吧，看半平面吧）直线根本和半平面交部分没有任何接触，此时我们称其为无用直线，直接弹出，然后接着判断。

然后这样不断的判断下去，最终直线和其相邻间的交点便会长的像凸包一样。

这就是粗略的做法，但是其是极其不完善的，甚至普通情况都难以处理，下面开始讲解不同情况以及其处理手法。

对于栈中元素更加形象的存储和讲解方式

哇，日报中讲的模型是真的直观易懂。

这里先说以下，如果(A_{i}) ~ (A_{j})都交于一个点的话，那么只保留(A_{i})，(A_{j})，方便下文讨论，在你看懂之后，再将其加入回来再思考一波正确性，你会发现其完全不会影响我们的讨论，可以让讨论存在的争议更少。

我们先将存下的直线想象成一条由一段段线段组成的 "链"。

或者具体地来讲，是：

链由一组有向线段 (v_1, v_2, v_3, ..., v_n) 组成，并满足 (v_1) 的结尾点是 (v_2) 的起始点， (v_2) 的结尾点是 (v_3) 的起始点，...，$ v_{n-1}$ 的结尾点是 (v_n) 的起始点，同时这个序列的极角递增（这里也可以反着定义递减，下面的说明类似），且满足最后一个元素的极角与第一个元素的极角差不超过 (2π)（弧度制），这里并不明确头尾元素的长度。

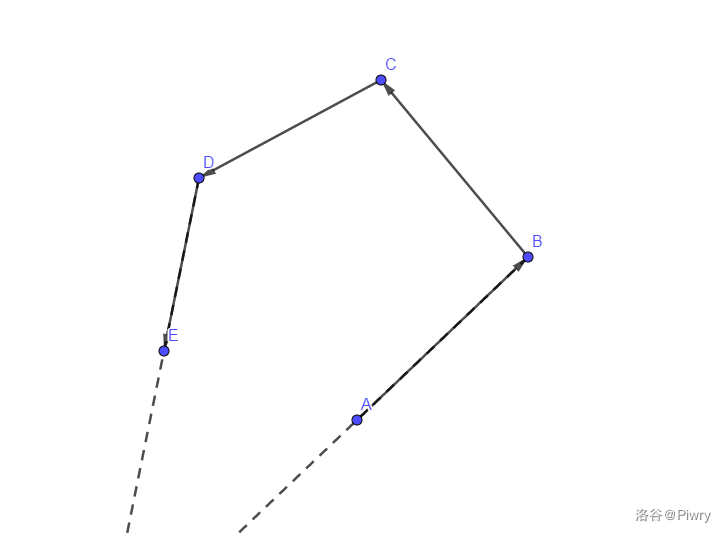
而这里，除了(v_{1})和(v_{n})以外的点都是相邻直线的交点，而其的有向线段就是有向直线与半平面交接触的部分。

而(v_1,v_n)吗，还记得最后一句话吗？这里并不明确头尾元素的长度，这个是什么意思？因为我们只是处理了每条直线和(top)以及(top-1)的关系，而没有处理头尾元素的关系，所以我们认为首尾元素与半平面交的部分接触的长度是无限的，因此，我们可以认为，(v_{1})和(v_{2})所代表的有向直线是(A_{1})，(v_{n-1})和(v_{n})所代表的有向直线是(A_{top})，而(v_{1})和(v_{n-1})则是满足上面两个要求的任意点。

我们成功的把半平面交的模型转换成容易理解的长得像凸包的模型。

环的出现及处理

在跑完半平面后，若是有交情况，就要考虑环的处理了。

而其说的环是什么呢？

额，我猜日报所说的环分三种：

1. 原本模型中的有向线段（不包括(v_{1}->v_{2})和(v_{n-1}->v_{n})）的出现了交点，存在环，即下图的情况四。

2. 原本的有向线段不存在交点，但栈底或者栈顶的直线与有向线段（不包括(v_{1}->v_{2})和(v_{n-1}->v_{n})）存在交点，即为情况(2,3)

3. 以上两种情况都不存在，且栈底和栈顶直线存在交点。

   

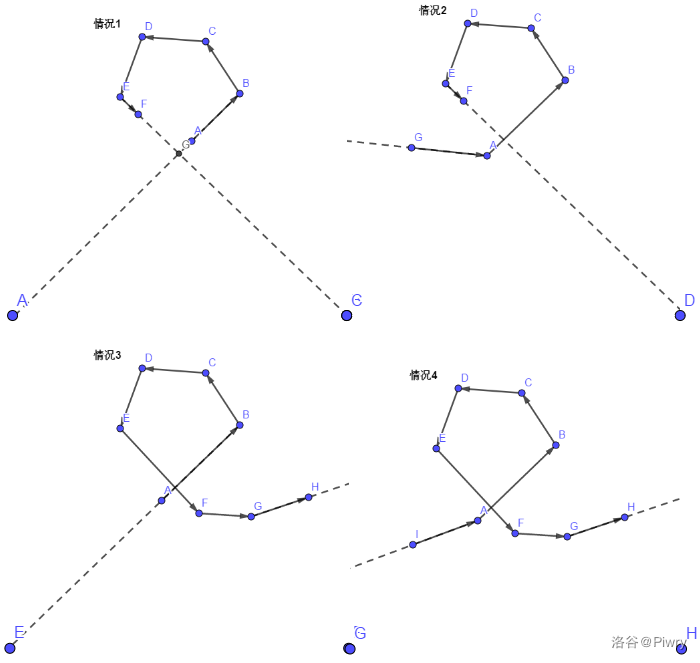
总之你会发现，就是栈顶和栈底这两种情况疯狂的出问题。

其实我们会发现，情况(1)就是我们想要的结果，但是(2,3,4)都出现了无用的有向线段（也就是无用的有向直线，你是可以证明这些无用的有向线段所代表的直线也是无用的）。

这个时候我们发现，栈底的元素也是可能存在问题的，不妨将其换为双端队列（只不过插入时能看成栈）。

首先可以看出对于 [情况2], [情况3]，只要判断线段的交点在不在 队尾、队头 元素的右侧即可。

/*情况2*/
while(l < r-1 && onright(hull[r-1], getIntersection(hull[l], hull[l+1]))) ++l;
/*情况3*/
while(l < r-1 && onright(hull[l], getIntersection(hull[r-1], hull[r-2]))) --r;

但是对于情况4呢？

其实你会发现：

onright(hull[r-1], getIntersection(hull[l], hull[l+1]))
onright(hull[l], getIntersection(hull[r-1], hull[r-2]))
//即上文的两个条件

情况4肯定满足其中一个。

你肯定会问，凭啥？

我们不妨把整个平面旋转，把(hull[l])变成(x)轴，方向为(x)负半轴的方向，这样保证了(hull[l])和(hull[l+1])的交点是在(x)轴上，且(hull[l])的半平面为(y≤0)，更加的方便讨论。

不妨通过构造反例来实现，首先(hull[r])与(hull[r-1])的交点必须在(y≤0)的部分。

不难发现，(hull[r])的极角绝对大于(0)好像这个没用，且无论怎么拖动被圈住的点，都一定满足(onright(hull[r-1], getIntersection(hull[l], hull[l+1])))

当然，你会发现严谨的证明我完全不会，但是感性的证明还是算比较直观的吧。

因此，你只要改造一下代码就能处理所有的情况。

while(l < r-1){
    if(onright(hull[r-1], getIntersection(hull[l], hull[l+1]))) ++l;
    else if(onright(hull[l], getIntersection(hull[r-1], hull[r-2]))) --r;
    else break;/*已经没有更新了*/
}

至此，如果有交，则已经处理完毕了。

无交情况判断

先默认无平行线段（即幅角之差的绝对值(=180°)和幅角相等的情况），后面讲。

无限交

无限交的情况是什么？

首先先讲一定有解的情况，还记得凸包的充要条件吗？

没错，就是满足那东西，还记得凸包的内角一定小于(180°)吗？所以相邻两条直线的幅角差的绝对值要小于(180°)，头尾的元素也是如此。

如果出现了(≥)的情况，说明交是无限交，那么如何判定此情况呢？

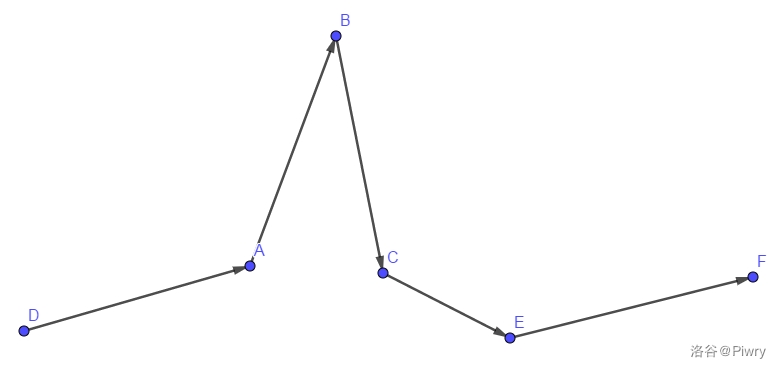
上图不满足极角排序

管他，旋转一下不就满足了

此时你会发现，其会在下述判定中直接把队列变成两个元素。

while(l < r-1){
    if(onright(hull[r-1], getIntersection(hull[l], hull[l+1]))) ++l;
    else if(onright(hull[l], getIntersection(hull[r-1], hull[r-2]))) --r;
    else break;/*已经没有更新了*/
}

因此，只要最后判断队列是否中小于等于两个元素即可（那有没有可能小于等于两个元素还有有限交的爬，都说了只是去掉无效元素，有效元素小于等于2个怎么可能有限交）。

但是如果满足了队列中相邻两条直线的幅角差的绝对值要小于(180°)就一定有交吗？

废话，充要条件啊(╯‵□′)╯︵┻━┻。

当然，有时候还会出现头尾的情况，因此还要判断头尾的幅角差，不过要注意还要模(360°)（弧度制模(2pi)），不过一般不用判断，因为无限交的情况一般不会出现，因为会在一定的范围内（那为什么还要讨论有限交的情况，因为下文中的无交就是转换成这种情况，只不过不会转换乘头尾的情况罢了）。

无交的情况

首先，如果存在无交的情况，则一定存在一条(a_{i})，在其插入的时候，其半平面与当时的半平面交的交集为空（充要条件）。

即存在一条直线能够直接把队列踢到(l=r)（必要条件）。

好，接下来较为理性的证明，存在一条(a_{i})，在其插入的时候，其半平面与当时的半平面交的交集为空的充要条件是，(a_{i})与(hull[l])的幅角差的绝对值(≥180°)。

对于(hull[l])，传统异能，旋转到(x)轴，方向负半轴，那么对于幅角(<0°)的直线而言，其和(hull[l])的半平面的交集都一定包含点((INF,0))，所以其半平面交绝对不为空。

这样子的话，插入就一定存在两条相邻直线幅角差的绝对值大于等于(180°)，转换为上面的情况，直接判断即可。

平行的情况

为什么要特别的拿出来讲一下，

因为你还记得函数中有个求交点的吗？交点是处理不了平行的。

对于幅角相等的两条直线，如果不共线，一个必然淘汰另外一个，然后就不用求交点了，但是共线呢？

因此，半平面交还有一个骚操作，在半平面交极角排序时，默认半平面比较大的优先。

int cmp(line A, line B){
    if(eq(A.angle, B.angle)) return onright(B, A.u);/*有向直线最左的会排在最后面，并被保留*/
    else return (gtr(B.angle, A.angle));
}

然后在for循环插入中加入此语句。

while(i < totl-1 && eq(ls[i].angle, ls[i+1].angle)) ++i;/*去重*/

对于幅角之差的绝对值(=180°)的情况。

额。

如果有一条直线在这两条直线之间，那么队列中不相邻，也就不用考虑他们两个交点情况。

但是对于没有直线的情况呢？那么这个时候就会出现两种情况。

1. 无限交，这个时候只要在入队时暴力特判(hull[r])是否是平行的即可。
2. 无交，这个时候，就是下图的情况了。

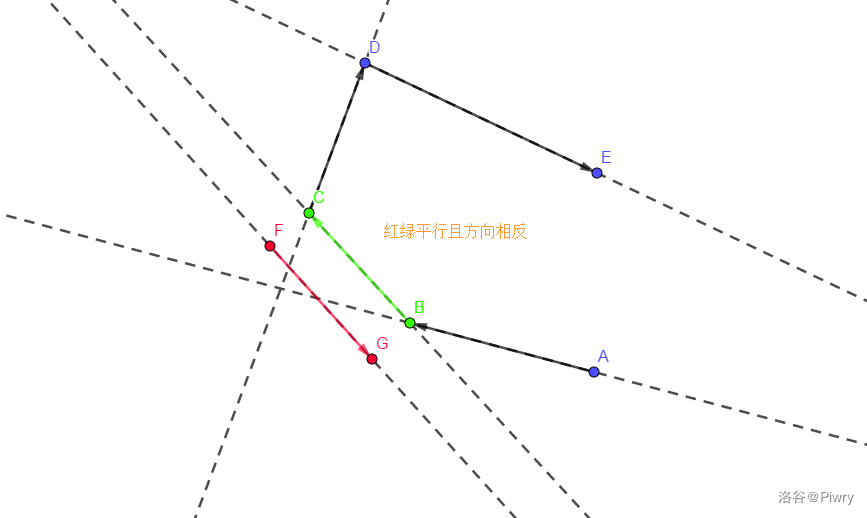
这个时候，不难发现的事情是，队列会一直踢出只剩队头，所以只需要在入队时判断(hull[r])是否是平行的即可。

当然，一般不存在无限交的情况，因为一般会限定在一个正方形内。

解集为点或者线段

还记得之前我说的如果交点在直线(a_{i})上，不弹出栈吗？就是为了应付这种情况的，如果在直线上弹出，那么就有可能导致这些情况被误判成无解。

但是在上述的证明中，又有可能会被理解为多条有向线段交于同一个点（实际上有向线段长度为(0)），因此交大家忽略掉(A_{l+1}) ~ (A_{r-1})的直线，但是如果你懂了证明，你会发现这些直线根本不会影响证明，删除与否根本无关，只不过删除了更加好的表述而已。

因此，你会发现，其实如果解集是点和线段可以视作无解的话，那么可以直接认为在交点在直线上可以直接弹出。（其实等价于认为半平面不包括直线。）

代码

时间复杂度：(O(nlogn))。

/*这里求得的交包括边界，主要取决于 onright() 函数*/
inline pad getHPI(line ls[], int totl, line hull[]){
    sort(ls, ls+totl, cmp);
    int l =0, r =0;
    for(int i =0; i < totl; ++i){
        while(i < totl-1 && eq(ls[i].angle, ls[i+1].angle)) ++i;/*去重*/
        while(r-l > 1 && onright(ls[i], getIntersection(hull[r-1], hull[r-2]))) --r;
        if(r > 0/*首次循环可能为空*/ && eq(ls[i].angle-hull[r-1].angle, pi)) return pad(0, 0);/*判平行的无交*/
        hull[r++] =ls[i];
    }
    while(r-l > 1){
        if(onright(hull[r-1], getIntersection(hull[l], hull[l+1]))) ++l;
        else if(onright(hull[l], getIntersection(hull[r-1], hull[r-2]))) --r;
        else break;/*已经没有更新了*/
    }
    if(r-l < 3) return pad(0, 0);
    else return pad(l, r);/*返回答案所在区间*/
}

另外一种双端队列的写法

讲解

这实际上更常用，但是上面一份代码的讲解更加直观。（好像上面的做法叫标准增量法，这个叫标准双端队列做法）

如果我们在插入的时候不是利用类似栈的形式，而是充分发挥队列的优势呢？

什么意思呢？为什么会产生第(4)种情况？如果我们在他还是第(2)种情况时就马上变成第一种情况，那么他最后不就只剩下第(1,3)种情况了吗？因此由此产生了在判断完队尾后判断队首的情况，最后只需要判断第(3)种情况即可。

/*这里求得的交包括边界，主要取决于 onright() 函数*/
inline pad getHPI(line ls[], int totl, line hull[]){
    sort(ls, ls+totl, cmp);
    int l =0, r =0;
    for(int i =0; i < totl; ++i){
        while(i < totl-1 && eq(ls[i].angle, ls[i+1].angle)) ++i;/*去重*/
        while(r-l > 1 && onright(ls[i], getIntersection(hull[r-1], hull[r-2]))) --r;
        while(r-l > 1 && onright(ls[i], getIntersection(hull[l], hull[l+1]))) ++l;
        if(r-l > 0/*首次循环可能为空*/ && eq(ls[i].angle-hull[r-1].angle, pi)) return pad(0, 0);/*判平行的无交*/
        hull[r++] =ls[i];
    }
    while(r-l > 2 && onright(hull[l], getIntersection(hull[r-1], hull[r-2]))) --r;/*仅弹出队尾即可*/
    if(r-l < 3) return pad(0, 0);
    else return pad(l, r);/*返回答案所在区间*/
}

代码会出的问题

考虑调换下列代码的先后顺序：

while(r-l > 1 && onright(ls[i], getIntersection(hull[r-1], hull[r-2]))) --r;
while(r-l > 1 && onright(ls[i], getIntersection(hull[l], hull[l+1]))) ++l;

变成：

while(r-l > 1 && onright(ls[i], getIntersection(hull[l], hull[l+1]))) ++l;
while(r-l > 1 && onright(ls[i], getIntersection(hull[r-1], hull[r-2]))) --r;

这样竟然会错？

其实一般情况下是不会错的，但是有一种情况会错，就是直接把队列弹出到只剩(l=r)的情况，这种情况，下面的写法会导致错误，首先，很明显的一个事情是，这样子可能会导致无交的情况直接变成头尾幅度差大于等于(180°)的无限交的情况，但是常规的代码一般不会判断这种情况，固会导致错误。

无限交情况省略我没细想，大致差不多吧。

此处采用wjyyy的证明：

更加一般的有限交情况，其也会在把队列弹出到只剩(l=r)的情况出错。

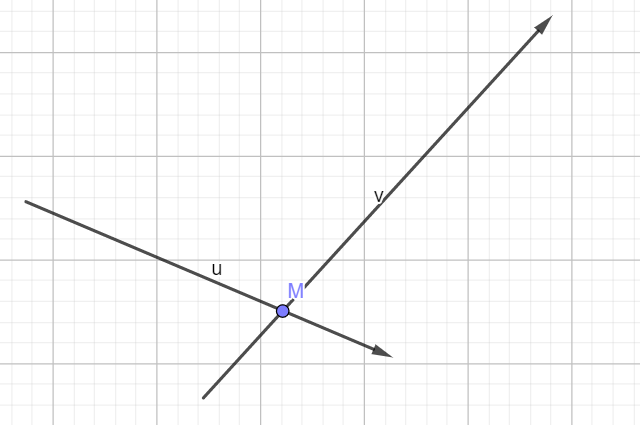
一般情况下，我们在队列 (队列顺序为 (left{vec{u},vec{v} ight})) 后面加一条边（向量 (vec{w})），会产生一个交点 (N)，缩小 (vec{v})后面的范围。

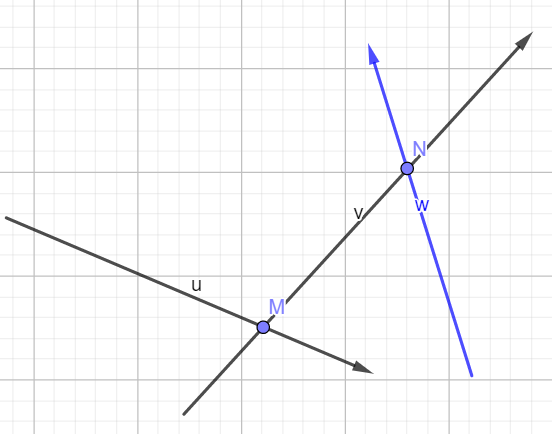
但是毕竟每次操作都是一般的，因此可能会有把 (M) 点“挤出去”的情况。

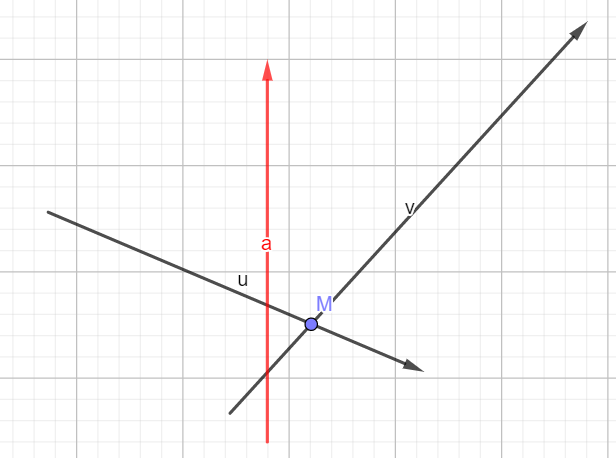
如果此时出现了向量 (vec{a}) ，使得 (M) 在 (vec{a}) 的右侧，那么 (M) 就要出队了。此时如果从队首枚举++l，显然是扩大了范围。实际上 (M)点是由 (vec{u}) 和 (vec{v}) 共同构成的，因此需要考虑影响到现有进程的是 (vec{u}) 还是 (vec{v})。而因为我们在极角排序后，向量是逆时针顺序，所以 (vec{v}) 的影响要更大一些。

就如上图，如果 (M) 确认在 (vec{a}) 的右侧，那么此时 (vec{v}) 的影响一定不会对半平面交的答案作出任何贡献。

而我们排除队首的原因是当前向量的限制比队首向量要大，这个条件的前提是队列里有不止两个线段（向量），不然就会出现上面的情况。

所以一定要先排除队尾再排除队首。（实际上排除了队首的情况基本上就是情况(2,4)了）

在线做法的idea

一下引用日报《对半平面交算法正确性解释的探索》的讲解：

现在考虑给已知半平面交添加一条有向直线的情况。

显然新交不包含新加入直线右侧的所有点（在直线上的点保不保留没大区别）。

同时，还发现这些点还满足：

1. 它们一定是在凸包边界上 "连续" 的一段
2. 我们将凸包所有边按极角排序，第一个极角大于和第一个极角小于插入直线的极角的两条边的交点一定是需要弹出的点（即使在最坏情况下（只弹出一个点））。

（如下图；对更多点情况可平移直线并由凸包性质发现）

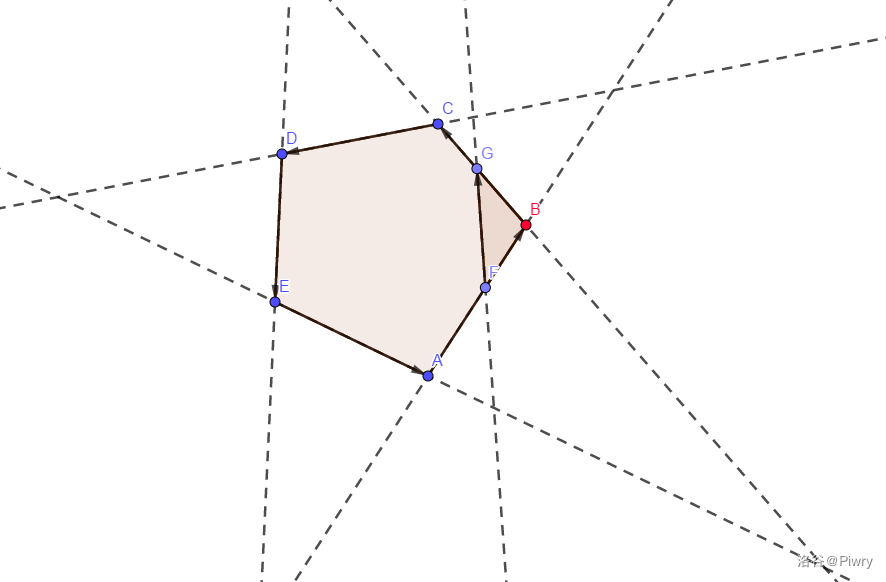
实现时，我们先按 性质二 尝试找到一个需要弹出的点。如果这个点不在加入直线的右侧，则这条直线就不会对交产生影响；否则只需逆/顺时针依次判断即可（这些点是相邻的），并对于一个方向在第一个不满足要求（在加入直线右侧）的点停下。

（至于点在当前直线上...其实这时候不特判去除也不会影响贡献。但在下一部分的做法中，不判这种情况可能会在某些特殊情况下出错）

同时，为了保证精度，我们仍保存加入直线的信息（通常用两个点表示直线...加入后并不重求点为交点），实际的凸包点在判断时求出。而直线删除的条件是它的两个交点都被弹出（一个交点被弹出的话保留，由于相邻的直线（边）被更新了，那个交点下次求出来也是不同的，就相当于弹出了）；同时注意对可能将所有直线弹出的加入操作（即无交）需要特判。（或者干脆存点...这段可以无视）

为了能支持二分查找而快速找到上述两条直线，保存的直线需按极角排序，考虑到还可能要在序列中间插入点，我们可能需要用平衡树来维护。

（由于在竞赛没什么实用价值代码就暂时咕咕了 QAQ （话说半平面交也真的常考吗...））

这种在线做法也可以很方便地改成离线。不过单纯照搬的话其实有很多部分是可以简化一下的。（其实这里应该早就有人看出这种做法和标准增量法很相似了...）

题目代码

多少年前的代码了

采用标准两端队列做法。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define  N  21000
#define  MAXN  100000
using  namespace  std;
double  eps=1e-8;
struct  dian
{
    double  x,y;
    dian(double  xx=0.0,double  yy=0.0){x=xx;y=yy;}
}pi[N];//点
inline  dian  operator-(dian  x,dian  y){return  dian(x.x-y.x,x.y-y.y);}
inline  dian  operator+(dian  x,dian  y){return  dian(x.x+y.x,x.y+y.y);}
inline  dian  operator*(dian  x,double  y){return  dian(x.x*y,x.y*y);}
struct  line
{
    dian  x,y;double  agr;
    void  set(double  x1,double  y1,double  x2,double  y2){x.x=x1;x.y=y1;y.x=x2;y.y=y2;agr=atan2(y2-y1,x2-x1);/*求角度*/}
}ss[N],li[N];int  head,tail,n,tp;
inline  double  mu(dian  x1,dian  x2,dian  y){return  (x1.x-y.x)*(x2.y-y.y)-(x2.x-y.x)*(x1.y-y.y);}//叉积
inline  double  muu(dian  x1,dian  x2){return  x1.x*x2.y-x2.x*x1.y;}//叉积
inline  dian  jd(line  x,line  y)
{
    double w =muu((y.y-y.x),(x.x-y.x))/muu((x.y-x.x),(y.y-y.x));
    return x.x+(x.y-x.x)*w;
}
inline  bool  safe(dian  x,line  y){return  mu(y.x,x,y.y)<=eps;}//在不在此半平面
inline  bool  cmp(line  x,line  y)//角度排序
{
    if(x.agr<y.agr)return  true;
    else  if(fabs(x.agr-y.agr)<=eps  &&  safe(x.x,y)==true/*如果同一个角度那么就判断哪个直线的半平面比较小（在有限范围内）*/)return  true;
    return  false;
}
void  HPI()
{
    sort(ss+1,ss+n+1,cmp);
    tp=1;for(int  i=2;i<=n;i++)if(ss[i].agr-ss[i-1].agr>eps)ss[++tp]=ss[i];//去重
    li[head=1]=ss[1];li[tail=2]=ss[2];n=tp;
    for(int  i=3;i<=n;i++)
    {
        while(head<tail  &&  safe(jd(li[tail],li[tail-1]),ss[i])==false)tail--;//踢队尾
        while(head<tail  &&  safe(jd(li[head],li[head+1]),ss[i])==false)head++;//踢队头
        li[++tail]=ss[i];//加入
    }
    while(head<tail  &&  safe(jd(li[tail],li[tail-1]),li[head])==false)tail--;//再来一次
    if(tail-head<2){printf("0.0
");return  ;}//无解
    int  pl=0;for(int  i=head;i<tail;i++)pi[++pl]=jd(li[i],li[i+1]);pi[++pl]=jd(li[head],li[tail]);//求出凸多边形
    double  ans=0;
    for(int  i=1;i<=pl;i++)ans+=mu(pi[i-1],pi[i],pi[1]);//算面积
    if(ans<0)ans=-ans;
    printf("%.1lf
",ans/2.0);
}
int  main()
{
    scanf("%d",&n);
    ss[1].set(MAXN,MAXN,-MAXN,MAXN);ss[2].set(-MAXN,MAXN,-MAXN,-MAXN);
    ss[3].set(-MAXN,-MAXN,MAXN,-MAXN);ss[4].set(MAXN,-MAXN,MAXN,MAXN);n+=4;//添加四条直线，因为题目添加了，所以不用考虑无限的情况
    for(int  i=5;i<=n;i++)
    {
        double  x1,y1,x2,y2;scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        ss[i].set(x1,y1,x2,y2);
    }
    HPI();
    return  0;
}

一道练手题

小凸想跑步

博客

根据古典概形得知，概率就是(P)点的可行位置的面积(÷)操场面积。

对于凸多边形的每条线段，推导其和(0-1)边面积之间的不等式，如果是解集是个半平面，则使用半平面交（事实证明单个不等式的解集确实是半平面）。

设是(i-(i+1))的边和(0,1)边进行讨论，利用叉积算面积列出(P)的不等式：

((x_1-x_0)(y_P-y_0)-(y_1-y_0)(x_P-x_0)≤(x_{i+1}-x_i)(y_{P}-y_i)-(y_{i+1}-y_i)(x_P-x_{i}))

(-(x_1-x_0)y_0+(x_1-x_0)y_P-(y_1-y_0)x_P+(y_1-y_0)x_0≤(x_{i+1}-x_i)y_{P}-(x_{i+1}-x_i)y_i-(y_{i+1}-y_i)x_P+x_{i}(y_{i+1}-y_i))

((y_{i+1}-y_i-y_1+y_0)x_{P}+(x_{1}-x_0+x_{i}-x_{i+1})y_{P}+(x_0y_1-x_1y_0+x_{i+1}y_i-y_{i+1}x_{i})≤0)

注：因为是逆时针给出点，所以叉积为正，所以直接这样列不等式。

PS：许多人说是(<)号，但是我JO得说他是最小的，但是没说最小是唯一的啊，所以个人觉得是(≤)这个得看对最小的定义是什么，当然，不管(<)还是(≤)，也就差直线这么一个面积，但是直线的面积可以是为(0)，因此怎么看都不会错。

不难发现，是形如：(ax+by+c≤0)的形式，因此是半平面，用半平面交求解集面积（当然，别忘了半平面是限定在一个凸包当中的）。

因此，我们就得到了其解析式，但是换成有向直线呢？

随便啦，自己想象就知道啦。（看代码也不难理解啦）

时间复杂度：(O(nlogn))。

PS：这里点的下标从(1)开始，而不是从(0)开始。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define  N  110000
#define  NN  210000
using  namespace  std;
double  eps=1e-6;
struct  dian
{
	double  x,y;
	dian(double  xx=0,double  yy=0){x=xx;y=yy;}
};
inline  dian  operator+(dian  x,dian  y){return  dian(x.x+y.x,x.y+y.y);}
inline  dian  operator-(dian  x,dian  y){return  dian(x.x-y.x,x.y-y.y);}
inline  dian  operator*(dian  x,double  y){return  dian(x.x*y,x.y*y);}
inline  double  operator/(dian  x,dian  y){return  (x.x*y.y-x.y*y.x);}//叉积
struct  line
{
	dian  x,y;double  arg;
	void  set(){arg=atan2(y.y-x.y,y.x-x.x);}//atan2算极角
}li[NN],st[NN]/*队列*/;int  len,head,tail;
inline  dian  operator*(line  x,line  y)//求两线交点 
{
	double  tt=((y.y-y.x)/(x.x-y.x))/((y.y-y.x)/(x.x-x.y));
	return  x.x+(x.y-x.x)*tt;
}
inline  bool  eq(double  x,double  y){return  (x-y)<=eps  &&  (x-y)>=-eps;}//判断x==y的 
inline  bool  safe(line  x,dian  y){return  (x.y-x.x)/(y-x.x)>0;}//左边为safe 
inline  bool  cmp(line  x,line  y)
{
	if(!eq(x.arg,y.arg))return  x.arg<y.arg;
	else  return  safe(x,y.x);
}
double  BPMJ()
{
	sort(li+1,li+len+1,cmp);
	head=1;tail=0;
	for(int  i=1;i<=len;i++)
	{
		while(i<len  &&  eq(li[i].arg,li[i+1].arg))i++;
		while(head<tail  &&  !safe(li[i],st[tail]*st[tail-1]))tail--;
		while(head<tail  &&  !safe(li[i],st[head]*st[head+1]))head++;
		if(head<=tail  &&  eq(li[i].arg-st[tail].arg,3.141592653))return  0;
		st[++tail]=li[i];
	}
	while(head+1<tail  &&  !safe(st[head],st[tail]*st[tail-1]))tail--;
	if(tail-head<=1)return  0;
	double  ans=0;
	dian  ji=st[tail]*st[head];
	for(int  i=head+1;i<tail;i++)ans+=((st[i-1]*st[i])-ji)/((st[i]*st[i+1])-ji);
	return  ans/2;
}
dian  sh[N];
int  n;
int  main()
{
	scanf("%d",&n);
	for(int  i=1;i<=n;i++)
	{
		scanf("%lf%lf",&sh[i].x,&sh[i].y);
	}
	len=n;sh[n+1]=sh[1];
	for(int  i=1;i<=n;i++)li[i].x=sh[i],li[i].y=sh[i+1],li[i].set();//限定在凸包范围
	double  ans=0;
	for(int  i=2;i<n;i++)ans+=(sh[i]-sh[1])/(sh[i+1]-sh[1]);//算凸包面积
	ans/=2;
    //转换部分
	for(int  i=2;i<=n;i++)
	{
		double  a=(sh[i+1].y-sh[i].y-sh[2].y+sh[1].y),b=(sh[2].x-sh[1].x+sh[i].x-sh[i+1].x),c=(sh[1].x*sh[2].y-sh[2].x*sh[1].y+sh[i+1].x*sh[i].y-sh[i].x*sh[i+1].y);
		if(eq(a,0)  &&  eq(b,0))
		{
			if(c>=0)
			{
				printf("0
");
				return  0;
			}
			continue;
		}
		if(eq(b,0)==1)
		{
			len++;
			if(a>=0)li[len].x=dian(-c/a,1),li[len].y=dian(-c/a,2);
			else  li[len].x=dian(-c/a,2),li[len].y=dian(-c/a,1);
			li[len].set();
			continue;
		}
		if(b<=0)
		{
			len++;
			li[len].x=dian(1,-(a+c)/b);li[len].y=dian(2,-(2*a+c)/b);
		}
		else  if(b>0)
		{
			len++;
			li[len].x=dian(2,-(2*a+c)/b);li[len].y=dian(1,-(a+c)/b);
		}
		li[len].set();
	}
	ans=BPMJ()/ans;
	printf("%.4lf
",ans);
	return  0;
}

小结

真恶心