参考资料与前话
luogu题解
伍昱奆佬的PPT Orz
顺便说一下,如果看这篇文章的人有一些较高深的2-sat姿势如果可以的话发个评论,感觉我这篇文章比较浅。
由于证明总是很难一块讲完讲另一块,都是互相息息相关的,所以有的证明有时候是有误在后面再根据已经讲的漏洞修改,希望大家习惯。
sat问题简介
以前,你妈总是问你哪个是对的,哪个是错的,现在,老师也总是问你,哪个是对的,哪个是错的。
不过不再是1+1=2是不是对的这种幼稚的问题,而是对于一些不知道具体内容的命题,只知道他们之间存在一些逻辑问题,让你判断他们的真假。
现在有很多命题(q_1,q_2,q_3...,q_n)
给你一些他们的逻辑关系:
(q_i) (or) (q_j=0)
(q_k) (and) (q_k=1)
.......
然后判断每个命题的真假,这种问题就叫sat问题。
特别的,如果对于所有的逻辑关系的式子中如果都是(k)个元的,那么就是(k-sat)问题。
当然,已经有人证明了(k-sat(k>2))的问题是NPC问题。
不过(k=2)反倒是个特例,我们把他们叫做(2-sat)问题。 这个问题是可以线性解决的。
曾经我看到一个奆佬说过:含有一定结构的 n-SAT 问题可以被新的 SAT solver 挺快的解决,但是完全随机的 n-SAT 问题就很难解决。
这个问题,我们讨论的就是(2-sat)问题。
解法
例题
万能的luogu
解法以及一点点证明
基本的转换思路
这里,我们仅仅讨论例题里面涉及的逻辑关系,其他的都自己想吧(╯‵□′)╯︵┻━┻。
现在题目基本上就是给你(a) (or) (b=1),然后进行判断。
但是需要注意一个事情,就是是可以(a) (or) (a=1/0),也就是指定了(a)一定是(0/1)了。
(2-sat)和差分约束一样都是利用构图来完成的,(2−sat)基本思路是拆点,我们先把第(i)个命题拆成(x_{i})和(!x_{i}) (一下规定,如果带有(x_i)表示的是(1),(!x_i)是(0),但如果是对于一个点(a),(!a)则是(a)所属命题的另外一个值),如果我们选了(x_i)就是这个命题为(1),选(!x_{i})就表示这个命题为(0),我们现在规定如果存在一条边,(a->b),那么就表示如果我们选了(a),那么也必须一起把(b)选了。
那么什么情况下某种方案不成立呢?简单明了,如果(x)和(!x)同时被选中不就是这种方案不成立了吗。
基本的构图
也许许多人看到这个定义是蒙的,这个要怎么构图?
举个例子其他自己推吧。
(q_x) (or) (q_y=1)
那么就表示(x,y)里面至少要有一个选(1)号点,也就是说如果我的(x)命题选了(0),(y)必须选(1),反之也是如此。
也就是(!x_{x}->x_y,!x_y->x_x)。
其他的自己推,当然也有一个特例,就是(q_i) (or) (qi=1),也就是必须为(1)。
我们从建图的角度讲,我们就是要让图里面每次选到(!x_{i})都不成立,不成立的条件是什么呀?
不就是两个点都被选到吗,那么只要(!x_i->x_i),不是就可以保证(!x_i)绝对不成立了吗?
至此,建图讲完了。
基础解法1
这个解法其实就是暴力,超级的暴力,对于每个点,如果(0)或者(1)没被选到,就选它(0/1),然后让他跑一边DFS传递,如果没问题,就让他当(0/1)(经过的点不用重置),有问题,就将这次DFS所修改的点全部重置,然后跑另外一个值,都不成立,无解。
时间复杂度个人认为是(O(n^2)),但是常数小,思路简单。
证明1
如果你对解法1心存疑虑,那么多半是担心如果选(1)成立,就选(1),而不考虑(0),这个操作有没有可能有后效性。
这里画个图帮助大家理解一下这种冲突
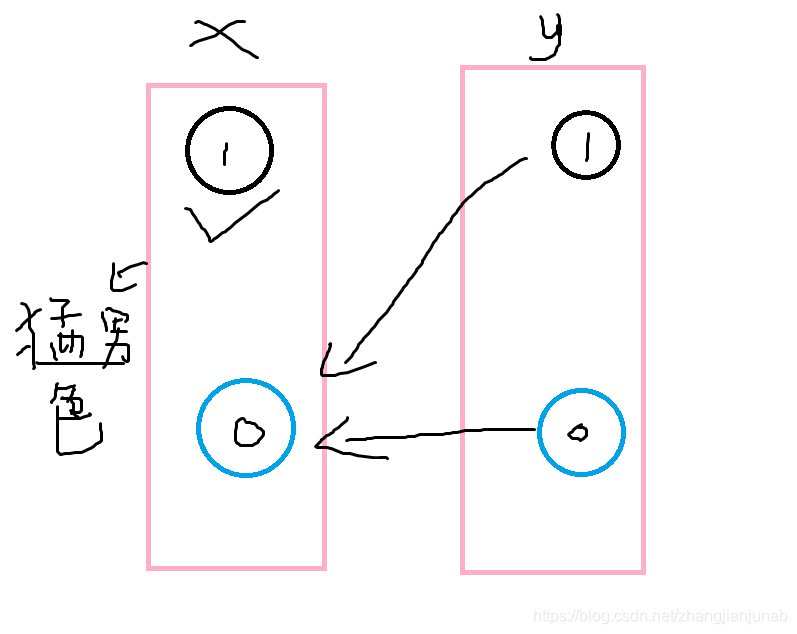
这个图一坨人会说,有解啊,(0,1)或(0,0),反正你开始选(1)就是个错误的选择,有后效性懂不懂!
但是对于(2-sat)问题,目前我所知道的操作都是对称的,也就是说若(a->b),则有(!b->!a),当然除了自己连自己以外(这个情况也是无伤大雅,不用理他),所以这个图要么不成立,要么少了两条边。
所以我们对于这个方法是错的的疑虑只是因为说怕选了(1)但是后面的点都是指向(0)的,但是你不曾考虑过如果后面有点指向(!x_i),(x_i)也会指回那个点的反点(即(!a)和(a)的关系)。
考虑(a->!x_i),那么(x_i->!a),所以不需要担心有后效性,因为我只要选了(1),(!a)点也会被选,怎么可能轮得到(a)来说话呢?
代码1
注:这份代码是把(x_i)当成(0)了。
#include<cstdio>
#include<cstring>
#define N 2100000
#define M 4100000
using namespace std;
struct node
{
int x,y,next;
}a[M];int len,last[N];
inline void ins(int x,int y)
{
len++;
a[len].x=x;a[len].y=y;a[len].next=last[x];last[x]=len;
}
int n,m,col[N]/*1表示被选,2表示等待选择*/;
int list[N],tail;
int fan(int x){return x>n?x-n:x+n;}
bool dfs(int x)//从x开始递归
{
if(col[x]==1)return true;
else if(col[fan(x)]==1)return false;
col[x]=1;list[++tail]=x;//以后方便回溯
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(dfs(y)==false)return false;
}
return true;
}
int ans[N];
int main()
{
// freopen("std.in","r",stdin);
// freopen("vio.out","w",stdout);我就是个SB东西,这都要对拍
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y,a,b;scanf("%d%d%d%d",&x,&a,&y,&b);
int xx=fan(x),yy=fan(y);
if(a==1)x^=xx^=x^=xx;
if(b==1)y^=yy^=y^=yy;
if(x==y)
{
if(a==b)ins(xx,x);
}
else ins(xx,y),ins(yy,x);//这个构图可以过,但是十分乱七八糟,如果你有更好的还是用自己的吧
}
for(int i=1;i<=n;i++)
{
if(col[i]==0 && col[fan(i)]==0)
{
tail=0;
if(dfs(i)==0)
{
while(tail)col[list[tail--]]=0;
if(dfs(i+n)==0)
{
printf("IMPOSSIBLE
");
return 0;
}
else ans[i]=1;
}
}
else ans[i]=(col[i]==0);
}
printf("POSSIBLE
");
for(int i=1;i<n;i++)printf("%d ",ans[i]);
printf("%d
",ans[n]);
return 0;
}
基础解法2
这个做法可就是线性(O(n))的了。
观察到一个强连通分量里面选了一个就全部都被选,那么我只需要作个tarjan缩点求出强连通不就简单很多了吗。
这里科普一下强连通的联通块编号其实就是拓扑序的反序,即入度为(0)的编号最大。
这里随便乱说一通,说错了证明供上
如果(a)和(!a)在一个联通块,当场无解, 然后对于(a)和(!a),哪个所在的拓扑序编号大选哪个(代码表现为所在连通块编号越小选哪个)。
基础证明2
首先说明,对于(a->!a)这条边不影响我们考虑对称性是因为如果他影响我们考虑对称性即他有影响强连通的个数的话,那么就代表(a,!a)在一个联通块里面,就代表无解,而我们讨论的都是有解情况,直接忽视。
这里无聊的证明一个东西,就是在有解情况下,一个点的联通块及其反点的联通块的点的个数相同,且里面每个点都能在对面集合找到自己的反点。
这个运用对称性好好想想就知道了。
这里上个图:
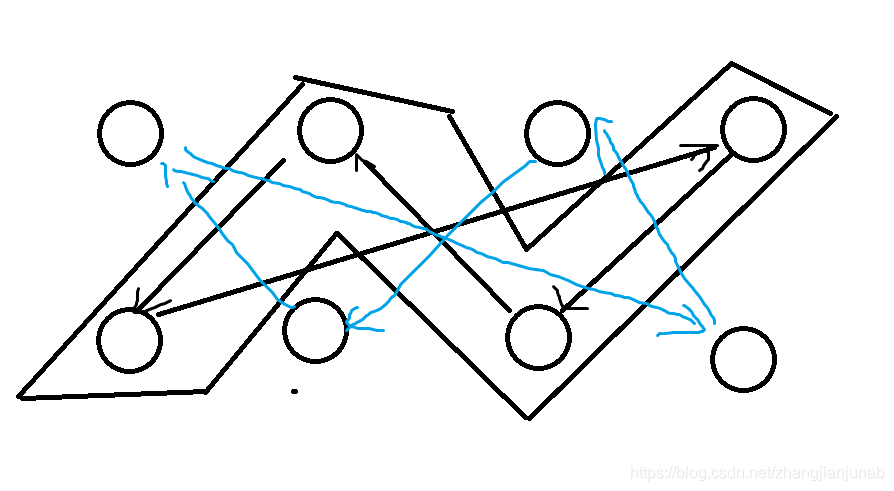
那联通块编号是拓扑序反序又是怎么理解啊。
脱开2-sat,放到一般图中:
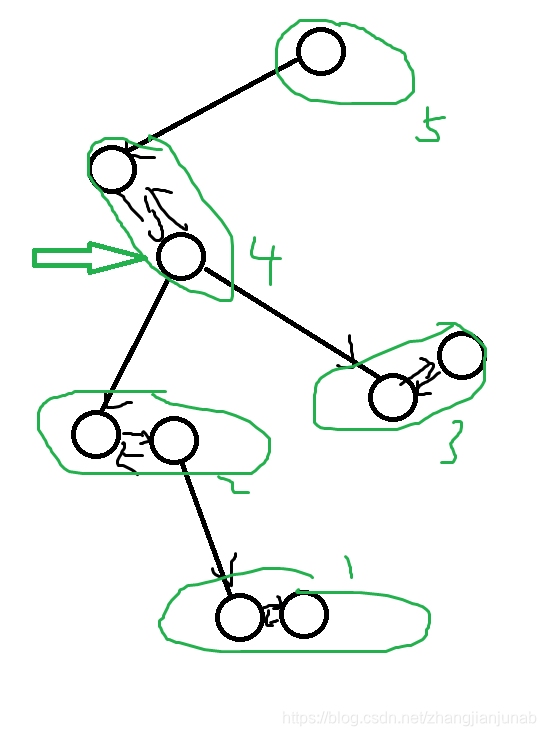
拓扑序满足的是什么,对于一个点(a),指向(a)的点(b)的拓扑序肯定在(a)之前,但是(tarjan)刚好满足的是若(b->a)且(a,b)不同联通块,则(a)的联通块编号肯定比(b)小,所以刚好相反。
好了,现在证明最后一句话,为什么选拓扑序大的,也就是为什么选这个点所在联通块TJ(tarjan)序小的。
我们先假设(x)的拓扑序大于(!x),这样(x)是会被选择的,但是我们需要证明(x)能到达的点都被选了。
开始证明:
假设(x)的拓扑序小于(!x)(反过来,方便打符号),这样选的是(!x),设能走到(x)点的点为(y),那么需要证明,(y)也不会被选。
因为(y)的拓扑序小于(x)小于(!x)小于(!y),所以只会选择(!y),不会选择(y)。
至于拓扑序相等的情况,随便选一个就行了,(x->!x)的情况,无伤大雅,只要不影响对称性即可。
代码2
#include<cstdio>
#include<cstring>
#define N 2000050
using namespace std;
inline void myre(int &x)
{
x=0;char c=getchar();
while(c>'9' || c<'0')c=getchar();
while(c>='0' && c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
}
struct node
{
int y,next;
}a[N];int len,last[N];
void ins(int x,int y)
{
len++;
a[len].y=y;a[len].next=last[x];last[x]=len;
}
int n,m,vis[N],sta[N],num,scc[N]/*所在的联通块*/,tim,list[N],top;
inline int mymin(int x,int y){return x<y?x:y;}
void dfs(int x)
{
vis[x]=sta[x]=++tim;list[++top]=x;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(!vis[y])
{
dfs(y);
vis[x]=mymin(vis[x],vis[y]);
}
else if(!scc[y])vis[x]=mymin(vis[x],sta[y]);
}
if(vis[x]==sta[x])
{
num++;scc[x]=num;
while(list[top]!=x)scc[list[top]]=num,top--;
top--;//把自己除出去
}
}
inline int fan(int x){return x>n?x-n:x+n;}
int main()
{
myre(n);myre(m);
for(int i=1;i<=m;i++)
{
int x,y,a,b;myre(x);myre(a);myre(y);myre(b);
int xx=fan(x),yy=fan(y);
if(a==1)xx^=x^=xx^=x;
if(b==1)yy^=y^=yy^=y;
if(x==y)
{
if(a==b)ins(xx,x);
}
else ins(xx,y),ins(yy,x);
}
for(int i=1;i<=2*n;i++)
{
if(!scc[i]/*没有阵营*/)dfs(i);
}
//全部都分好了阵营。
for(int i=1;i<=n;i++)
{
if(scc[i]==scc[fan(i)])
{
printf("IMPOSSIBLE
");
return 0;
}
}
printf("POSSIBLE
");
for(int i=1;i<=n;i++)
{
if(scc[i]<scc[fan(i)])//拓扑序小的先
{
printf("0 ");
}
else printf("1 ");
}
return 0;
}
小结
没做什么题目,溜了溜了。