烦人的树链剖分
说实话我是真的烦树链剖分,因为代码太长了。
这里的层数低指的是离根节点越近。
例题
题面
时间限制: 1 Sec 内存限制: 128 MB
【题意】
给出一棵有N个点的树,每个点都有一个值ai,两种操作:
1、U x y:修改第x个点的值为y;
2、Q x y:求第x个点到第y个点路径上所有点(包含x和y)的最大值
【输入格式】
第一行输入N和M(0<N<=200000,0<M<=100000),N表示有N个点,M表示有M个操作
下来N个点的值。
下来N-1条边(x y)。
然后是M个操作。
【输出格式】
遇到Q操作的时候,输出结果。
【样例输入】
5 6
2 4 5 8 7
1 2
3 4
4 1
5 3
Q 1 5
U 3 9
Q 1 5
Q 4 5
U 2 13
Q 1 5
【样例输出】
8
9
9
9
思路
首先,给出一棵树,我们定义一个节点的重儿子,这个重儿子的子树节点个数是这个节点所有儿子子树中最大的,重儿子在下文称作重节点。
而由重节点连向父亲的边构成的一条链叫重链,其他不是重边的轻边组成的叫轻链,重链可以只有一个不是重节点的节点构成(也就是说每个点都在一个重链上),但是这个点应该也会在一个轻链上。
红色重链,蓝色轻链,有颜色填充的表示成为重节点:
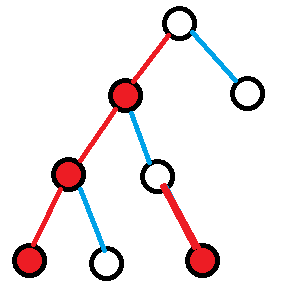
然后我们再对原树的每个节点进行标号,优先标每个节点的重儿子,那么我们就会发现每个重链的编号竟然是连续的!!!
那么我们自然而然想到了用线段树来维护每条重链的信息。
但是我们有了两个点又要怎么跳呢?
我们有了两个点(x,y),那么我们先查询(x,y)所在的重链的层数最小的点(tx,ty),看看谁的层数更高我们跳谁,顺带查询,跳是跳到重链祖先的父亲上,然后知道(x,y)在同一条重链上,然后终结之跳,改就直接改,害怕什么?
#include<cstdio>
#include<cstring>
using namespace std;
const int cc=210000;
const int pp=410000;
inline int mymax(int x,int y){return x>y?x:y;}
inline void swap(int &x,int &y){int tt=x;x=y;y=tt;}
struct node
{
int y,next;
}a[pp];int len=0,last[cc];
int b[cc],n,m;
void ins(int x,int y)
{
len++;
a[len].y=y;a[len].next=last[x];last[x]=len;
}
struct trnode
{
int l,r,lc,rc,c;
}tr[pp];int trlen=0;
int fa[cc],son[cc],tot[cc],dep[cc];
int z,top[cc],ys[cc],yss[cc];
void bt(int l,int r)
{
trlen++;int now=trlen;
tr[now].l=l;tr[now].r=r;
if(l==r)tr[now].c=b[yss[l]];
else
{
int mid=(l+r)/2;
tr[now].lc=trlen+1;bt(l,mid);
tr[now].rc=trlen+1;bt(mid+1,r);
tr[now].c=mymax(tr[tr[now].lc].c,tr[tr[now].rc].c);
}
}
void change(int now,int x,int k)
{
if(tr[now].l==tr[now].r){tr[now].c=k;return ;}
int lc=tr[now].lc,rc=tr[now].rc,mid=(tr[now].l+tr[now].r)/2;
if(x<=mid)change(lc,x,k);
else if(mid+1<=x)change(rc,x,k);
tr[now].c=mymax(tr[lc].c,tr[rc].c);
}//线段树的修改
int findmax(int now,int l,int r)
{
if(tr[now].l==l && tr[now].r==r)return tr[now].c;
int lc=tr[now].lc,rc=tr[now].rc,mid=(tr[now].l+tr[now].r)/2;
if(r<=mid)return findmax(lc,l,r);
else if(mid+1<=l)return findmax(rc,l,r);
else return mymax(findmax(lc,l,mid),findmax(rc,mid+1,r));
}//线段树的查询
void dfs1(int x)
{
tot[x]=1;son[x]=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(dep[y]==0)
{
dep[y]=dep[x]+1;
fa[y]=x;
dfs1(y);
son[x]=tot[son[x]]<tot[y]?y:son[x];
tot[x]+=tot[y];
}
}
}//先建树
void dfs2(int x,int tp)
{
top[x]=tp;ys[x]=++z;yss[z]=x;
if(son[x]!=0)dfs2(son[x],tp);
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(y!=son[x] && y!=fa[x])dfs2(y,y);
}
}//再给新编号
int solve(int x,int y)//查询
{
int tx=top[x],ty=top[y],ans=0;
while(tx!=ty)
{
if(dep[tx]>dep[ty])swap(tx,ty),swap(x,y);
ans=mymax(ans,findmax(1,ys[ty],ys[y]));
y=fa[ty];ty=top[y];
}
if(dep[x]>dep[y])swap(x,y);
return mymax(ans,findmax(1,ys[x],ys[y]));
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
for(int i=1;i<n;i++)
{
int x,y;scanf("%d%d",&x,&y);
ins(x,y);ins(y,x);
}
dep[1]=1;fa[1]=0;dfs1(1);
dfs2(1,1);bt(1,z);
while(m--)
{
char ss[5];int x,y;scanf("%s%d%d",ss,&x,&y);
if(ss[0]=='Q')printf("%d
",solve(x,y));
else change(1,ys[x],y);
}
return 0;
}
无脑喷不要吐槽没注释,毕竟这些东西看就完事了,要什么注释,又不是什么特别难理解的东西。
树链剖分同时也有这两种性质
1,如果((u, v))是一条轻边,那么(size(v) < size(u)/2);
2,从根结点到任意结点的路所经过的轻重链的个数必定都小于(logn),因为每走一条轻边,子树大小就(/2),而每跳完一个重链,子树的大小也会(/2)甚至减的更小;
同时,有大佬证明,这种写法的时间复杂度是(O(mlogn^2))。(其实用性质2就证明出来了,因为还有个线段树呢)
要想学(O(mlogn))可以去看博客。
练习
1
【题目描述】
就是给出一个n个点(0~n-1) 的有根树(根为0),和q次操作;初始时树上所有结点权值均为0;
1、 操作将根到x结点的所有结点权值置为1,并输出这次操作有多少个元素的改变了状态;
2、操作将x结点的子树中所有结点权值置为0,并输出这次操作有多少个元素的改变了状态;(n,q<=100000)
【输入格式】
输入文件的第1行包含1个正整数n。随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,…,n−2,n−1点的父亲节点。
接下来一行包含1个正整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
Install x:表示1操作
Uninstall x:表示2操作
对于每个操作,输出这步操作有多少个点改变了状态。
【输出格式】
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变状态的点数。
Sample Input
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
Sample Output
3
1
3
2
3
你以为很难?线段树维护一下0或者是1的个数。
而子树内的编号也是连续的。。。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int b[210000],n,m;
struct node
{
int y,next;
}a[410000];int len,last[210000];
void ins(int x,int y)
{
len++;
a[len].y=y;a[len].next=last[x];last[x]=len;
}
struct trnode
{
int l,r,lc,rc,c;//0的个数
}tr[410000];int trlen;
int tot[210000],son[210000],dep[210000],fa[210000];
int z,ys[210000],yss[210000],top[210000];
void bt(int l,int r)
{
trlen++;int now=trlen;
tr[now].l=l;tr[now].r=r;tr[now].c=0;
if(l==r)tr[now].c=b[yss[l]];
else
{
int mid=(l+r)/2;
tr[now].lc=trlen+1;bt(l,mid);
tr[now].rc=trlen+1;bt(mid+1,r);
tr[now].c=r-l+1;
}
}
int change(int now,int l,int r,int k)
{
int ans=0;
if(tr[now].l==l && tr[now].r==r)
{
if(k==0)ans=r-l+1-tr[now].c,tr[now].c=r-l+1;
else ans=tr[now].c,tr[now].c=0;
return ans;
}
int lc=tr[now].lc,rc=tr[now].rc,mid=(tr[now].l+tr[now].r)/2;
if(tr[now].c==tr[now].r-tr[now].l+1)
{
tr[lc].c=tr[lc].r-tr[lc].l+1;
tr[rc].c=tr[rc].r-tr[rc].l+1;
}
else if(tr[now].c==0)tr[lc].c=tr[rc].c=0;
if(r<=mid)ans=change(lc,l,r,k);
else if(mid+1<=l)ans=change(rc,l,r,k);
else ans=change(lc,l,mid,k)+change(rc,mid+1,r,k);
tr[now].c=tr[lc].c+tr[rc].c;
return ans;
}
void dfs1(int x)
{
son[x]=0;tot[x]=1;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
fa[y]=x;
dep[y]=dep[x]+1;
dfs1(y);
son[x]=tot[son[x]]<tot[y]?y:son[x];
tot[x]+=tot[y];
}
}
int ll[210000],rr[210000];
void dfs2(int x,int tp)
{
top[x]=tp;ys[x]=++z;yss[z]=x;ll[x]=z;
if(son[x]!=0)dfs2(son[x],tp);
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(y!=son[x])dfs2(y,y);
}
rr[x]=z;
}
int solve(int x)
{
int tx=top[x],ans=0;
while(x!=0)
{
ans+=change(1,ys[tx],ys[x],1);
x=fa[tx];tx=top[x];
}
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
int x;scanf("%d",&x);
ins(x+1,i);
}
dep[1]=1;dfs1(1);
dfs2(1,1);
bt(1,z);
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
char ss[20];int x;scanf("%s%d",ss,&x);x++;
if(ss[0]=='i')printf("%d
",solve(x));
else printf("%d
",change(1,ll[x],rr[x],0));
}
return 0;
}
2
题面
【题目描述】
Bob想要和Carrol玩游戏。但Carrol觉得玩游戏太无聊,就和Tuesday去写歌了。于是现在Bob来找你玩游戏。
这个游戏是这样的:给定一棵n个节点的树, 1号点为根节点,设v的父亲是f(v) 。其中每个节点有一个颜色,要么是黑色,要么是白色。不妨记第i个节
点的初始颜色是ci。ci =0或1,表示黑色或白色。
在游戏开始时,Bob为每个节点选择一个目标颜色di,要求你经过若干次操作,将每个节点变成其目标颜色。你的操作是这样的:
●选定一个点u,将u,f(u),f(f(u)),…,fk-1 (u)这k个节点的颜色翻转(将白色节点变为黑色节点,将黑色节点变为白色节点)。其中k是游戏开始前确定的一个正整数。
只有u,f(u),f(f(u)),…,fk-1 (u)这k个节点均存在,你才能执行这样的操作。当然,你可以执行任意多次操作。
现在Bob要和你玩T次这样的游戏,每次你都想要知道你是否有可能完成要求,即通过若干次操作,将所有节点变成其目标颜色。
【输入说明】
●第一行仅一个数T≤10,表示这样的游戏的次数;
●接下来共有T组数据。对于每一组数据:
○第一行是两个正整数n,k,n表示树的大小,k的含义请参见题目描述。
数据满足n,k≤2×10^5
○接下来n-1行每行两个数u,v,表示树上有一条边(u,v) 。注意:输入并不保证边的方向。
○接下来一行n个数c1 , c2,…,cn,表示初始颜色。
○接下来一行n个数d1 , d2,…,dn,表示目标颜色。
【输出说明】
输出包含T行,第i行对应第i次游戏的答案;
对于第i次游戏,如果你有可能完成任务,输出Yes,否则输出No 。
【样例输入】
2
3 2
1 2
2 3
0 0 0
1 0 1
3 2
1 2
2 3
0 0 0
1 1 1
【样例输出】
Yes
No
【样例解释】
●在第一个例子中,第一次选择2号点操作,1,2号点被翻转;第二次选择3
号点操作,2,3号点被翻转。即达成目标状态。
●可以证明,无法将初始状态经过操作变为目标状态。
【数据范围】
对于全部测试点:T≤10, k≤n≤2×10^5,保证数据给出的是一棵树。
对于前 10% 的数据,n≤5;
对于前 30% 的数据,n≤20;
对于前 50% 的数据,n≤2000;
对于前 70% 的数据,n≤50000;
对于全部数据,n≤2×10^5
题解
我们首先把一棵树自下往上考虑一下,如果这个节点不是目标状态,那么我们从这个节点开始往上翻转(k)个节点,然后如果层数不够的话就返回false,至于区间的问题的话不是一个树剖就能解决的事情了吗。
#include<cstdio>
#include<cstring>
#define N 210000
#define NN 410000
using namespace std;
int n,m;
int ys[N],yys[N],z,yss[N];
int aa[N];
struct node
{
int lc,rc,l,r,len,c;
bool vl;
}ttr[NN];int tlen;
void bt(int l,int r)
{
tlen++;int now=tlen;
ttr[now].l=l;ttr[now].r=r;ttr[now].c=0;ttr[now].lc=ttr[now].rc=0;ttr[now].c=0;ttr[now].vl=0;ttr[now].len=r-l+1;
if(l<r)
{
int mid=(l+r)/2;
ttr[now].lc=tlen+1;bt(l,mid);
ttr[now].rc=tlen+1;bt(mid+1,r);
ttr[now].c+=ttr[ttr[now].lc].c+ttr[ttr[now].rc].c;
}
else ttr[now].c+=aa[yys[l]];
}
inline void chu(int x){ttr[x].c=ttr[x].len-ttr[x].c;ttr[x].vl^=1;}
inline void pushdown(int x)
{
chu(ttr[x].lc);chu(ttr[x].rc);
ttr[x].vl=0;
}
void fanzhuan(int now,int l,int r)
{
if(ttr[now].l==l && ttr[now].r==r){chu(now);return ;}
if(ttr[now].vl)pushdown(now);
int lc=ttr[now].lc,rc=ttr[now].rc,mid=(ttr[now].l+ttr[now].r)/2;
if(r<=mid)fanzhuan(lc,l,r);
else if(mid<l)fanzhuan(rc,l,r);
else fanzhuan(lc,l,mid),fanzhuan(rc,mid+1,r);
ttr[now].c=ttr[lc].c+ttr[rc].c;
}
int findhaha(int now,int x)
{
if(ttr[now].c==ttr[now].len || !ttr[now].c)return ttr[now].c>0;
if(ttr[now].vl)pushdown(now);
int lc=ttr[now].lc,rc=ttr[now].rc,mid=(ttr[now].l+ttr[now].r)/2;
if(x<=mid)return findhaha(lc,x);
else return findhaha(rc,x);
}
//
struct bian
{
int y,next;
}a[NN];int len,last[N];
inline void ins(int x,int y){len++;a[len].y=y;a[len].next=last[x];last[x]=len;}
int dep[N],son[N],cnt[N],fa[N];
void dfs1(int x)
{
cnt[x]=1;son[x]=0;
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(fa[x]!=y)
{
dep[y]=dep[x]+1;fa[y]=x;
dfs1(y);
cnt[x]+=cnt[y];
cnt[y]>cnt[son[x]]?son[x]=y:0;
}
}
}
void dfs2(int x)
{
ys[x]=++z;yys[z]=x;
if(son[x])yss[son[x]]=yss[x],dfs2(son[x]);
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(fa[x]!=y && son[x]!=y)yss[y]=y,dfs2(y);
}
}
void fanzhuan(int x)
{
int z,la=m;
while(1)
{
z=yss[x];int ss;
if((ss=dep[x]-dep[z]+1)<la)fanzhuan(1,ys[z],ys[x]),x=fa[z],la-=ss;
else {fanzhuan(1,ys[x]-la+1,ys[x]);break;}
}
}
bool dfs3(int x)
{
for(int k=last[x];k;k=a[k].next)
{
int y=a[k].y;
if(y!=fa[x])
{
if(!dfs3(y))return false;
}
}
if(findhaha(1,ys[x]))
{
if(dep[x]+1<m)return false;
fanzhuan(x);
}
return true;
}
inline void gets(int &x)//看不见我QAQ
{
x=0;char c=getchar();
while(c>'9' || c<'0')c=getchar();
while(c<='9' && c>='0')x=(x<<3)+(x<<1)+(c^48),c=getchar();
}
int main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
int T;gets(T);
while(T--)
{
gets(n);gets(m);
len=0;memset(last+1,0,n<<2);z=0;tlen=0;
for(int i=1;i<n;i++)
{
int x,y;gets(x);gets(y);
ins(x,y);ins(y,x);
}
for(int i=1;i<=n;i++)gets(aa[i]);
for(int i=1;i<=n;i++)
{
int x;gets(x);
aa[i]^=x;//不一样为1,一样为0
}
dfs1(1);
yss[1]=1;dfs2(1);
bt(1,n);
if(dfs3(1))printf("Yes
");
else printf("No
");
}
return 0;
}
神仙算法LCT
也许许多人,会认为LCT是大佬算法,但是其实不是的,因为LCT其实挺暴力的,但是思路上还是十分的新奇,所以只能说你懂了会说很暴力,但是你不懂的话,你也会花一点的时间,不像带花树,你花了大量的时间,也不敢说他暴力吧。
例题
时间限制: 1 Sec 内存限制: 128 MB
【题意】
浅谈link Cut Tree实现及应用 陈漫璟
一个图,有n个点,一开始图中没有边。
三种操作:
Connect u v:在点u和点v之间建一条边。保证所有Connect操作不会重复建边。
Destroy u v:摧毁点u到点v之间的边。保证所有Destroy操作将摧毁的是一条存在的边。
Query u v:询问点u和点v是否联通,是输出Yes,否则输出No
保证:在任何时刻,任何点到任何点最多只有一条路径。(就是叫你用树咯)
【输入格式】
第一行为两个正整数n和m,分别表示点的个数和操作的个数。
以下m行,一行表示一个操作。
每行开头是一个表示指令种类的字符串s(区分大小写),之后有两个整数u和v (1≤u, v≤n且u≠v) 分别表示两个点的编号。
【输出格式】
对每个Query操作,输出点u和点v是否连通:是输出Yes,否则输出No。
【样例输入】
200 5
Query 123 127
Connect 123 127
Query 123 127
Destroy 127 123
Query 123 127
【样例输出】
No
Yes
No
【样例输入】
3 5
Connect 1 2
Connect 3 1
Query 2 3
Destroy 1 3
Query 2 3
【样例输出】
Yes
No
【数据说明 】
10%的数据满足n≤1000, m≤20000
20%的数据满足n≤2000, m≤40000
30%的数据满足n≤3000, m≤60000
40%的数据满足n≤4000, m≤80000
50%的数据满足n≤5000, m≤100000
60%的数据满足n≤6000, m≤120000
70%的数据满足n≤7000, m≤140000
80%的数据满足n≤8000, m≤160000
90%的数据满足n≤9000, m≤180000
100%的数据满足n≤10000, m≤200000
【来源】SDOI2008
思路
树链剖分是用重轻链分的,如果要改变树的形态的话,重轻链就可能会失去他原本的意义,导致时间复杂度退化。
那有没有什么可以动态划分的链呢?有,肯定有,就是传说中的虚实链,两个点的边可能是虚边,可能是实边,老规矩,一个点就是一个实链(在他不是其他实链的情况下),具体划分方式看后面。
首先,我们定义每一个实链(一开始是一个个点)都是一棵Splay(可以支持区间的树一般都可以),以层数为关键字,这棵Splay根节点指向的是这个实链层数最小的点的父亲,但是这个父亲所在的Splay不会认他做儿子。
而我们也规定这个Splay有以下的性质:
- 每个Splay里面不允许有层数相同的点。
- 维护的点层数严格从上往下递增(其实就是让你维护一条链)。
建链到根
之前说怎么划分实边虚边?就是在这个函数把一个点到根节点的边全部划成实边,如果一个点原本就和另一个儿子有一个实边的话,就变成虚边,但是怎么划分?
红色边实边,蓝色边轻边,方框框住的是棵Splay。
我们现在要把指到的点建链上去,首先我们肯定会改变Splay的样子的,那么也就是说我们需要把这个点splay上去,而为了后面函数的方便,我们要把这个点的所有与儿子相连的实边虚化,那么我们只需要把这个点旋上去,然后取消右儿子就行了(取消就是把右儿子等于0)。
然后我们会从Splay的根跳到上个实链的点(这个点是这个实链祖先的父亲),然后依旧把这个点原本的实链取消,然后连到原本的实链,使得两个实链合为一体。
这里要注意,取消与右儿子的关联就相当于在这个实链上把层数比根节点打的点踢出了这个实链。(但是踢掉的点本身还是个实链,只不过跟这个实链没有了关联)
怎么越来越感觉这是个小人画呢?
那么,我们的代码就出来了:
inline void ace(int x)
{
for(int y=0;x;x=tr[y=x].f)splay(x),tr[x].son[1]=y;//取消右儿子的关联,直接指向要指的点
}
//也许你会问为什么fa不=,因为原本就有
核心的换根操作
LCT最灵活的就是能把(x)变成根,在(log)的时间内,如何换根?
首先,我们肯定要(ace)一下(上个操作),然后再splay一下,那么目前这个Splay不就只有左子树了?因为这个点层数最大,那么我们可以把他换成层数最小的点呀,那不就是翻转一下吗?
而且其他的Splay的形态换根前后都不会变换,所以只用给这棵Splay打标记就行了。
inline void makeroot(int x)
{
ace(x);splay(x);
tr[x].sv^=1;
}
找根
找到这个LCT的根很简单,只要(ace)一下,然后splay一下,一直往左儿子跳,层数最小的点就是根了。
inline int findroot(int x)
{
ace(x);
splay(x);
int y=x;while(tr[y].son[0])y=tr[y].son[0],pushdown(y)/*因为在Splay中,x是绝对被pushdown了,但是不能保证y被pushdown了,但是有人不加pushdown过了。。。*/;
return y;
}
给x,y连边
我们只要(makeroot(x)),然后(fa[x]=y)就行了,当然,这样不就认为(y)所在的LCT的根是根了吗?是的,那又怎样呢。
inline void link(int x,int y)
{
makeroot(x);
tr[x].f=y;
}
分离x,y之间的链
我们只要(makeroot(x)),然后(ace(y))就行了,为了后面函数的方便,再(splay(x))。
inline void spilt(int x,int y)
{
makeroot(x);
ace(y);splay(x);
}
删x,y的边
分离边,然后把(x)的右儿子清零,把(y)的父亲清零。
inline void cut(int x,int y)
{
spilt(x,y);//x为根
tr[x].son[1]=0;tr[y].f=0;//断绝关系
}
另外Splay的里面别忘记判断一个点到底是不是根了(即是父亲的儿子)。
代码
#include<cstdio>
#include<cstring>
#define N 11000
using namespace std;
struct node
{
int f,son[2];bool sv;
}tr[N];
inline int chk(int x){return tr[tr[x].f].son[1]==x;}
inline bool nroot(int x){return (tr[tr[x].f].son[0]==x || tr[tr[x].f].son[1]==x);}//判断是不是根
inline void rotate(int x)
{
int f=tr[x].f,ff=tr[f].f,w=chk(x)^1,son=tr[x].son[w];
int r,R;
r=son;R=f;tr[r].f=R;tr[R].son[w^1]=r;
r=x;R=ff;tr[r].f=R;if(nroot(f))tr[R].son[chk(f)]=r;
r=f;R=x;tr[r].f=R;tr[R].son[w]=r;
}
inline void pushdown(int x)
{
if(tr[x].sv)
{
tr[x].sv=0;
tr[x].son[0]^=tr[x].son[1]^=tr[x].son[0]^=tr[x].son[1];
tr[tr[x].son[0]].sv^=1;tr[tr[x].son[1]].sv^=1;
}
}
int sta[N],len;
void splay(int x)
{
int y=x;sta[len=1]=x;
while(nroot(y))sta[++len]=y=tr[y].f;
while(len)pushdown(sta[len--]);//神奇的下传标记
while(nroot(x))
{
int f=tr[x].f,ff=tr[f].f;
if(!nroot(f))rotate(x);
else rotate(chk(x)^chk(f)?x:f),rotate(x);
}
}
inline void ace(int x)
{
for(int y=0;x;x=tr[y=x].f)splay(x),tr[x].son[1]=y;
}
inline void makeroot(int x)
{
ace(x);splay(x);
tr[x].sv^=1;
}
inline int findroot(int x)
{
ace(x);
splay(x);
int y=x;while(tr[y].son[0])pushdown(y),y=tr[y].son[0];
return y;
}
inline void link(int x,int y)
{
makeroot(x);
tr[x].f=y;
}
inline void spilt(int x,int y)
{
makeroot(x);
ace(y);splay(x);
}
inline void cut(int x,int y)
{
spilt(x,y);//x为根
tr[x].son[1]=0;tr[y].f=0;
}
int n,m;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
char st[20];scanf("%s",st+1);
int x,y;scanf("%d%d",&x,&y);
if(st[1]=='Q')
{
if(findroot(x)!=findroot(y))printf("No
");
else printf("Yes
");
}
else if(st[1]=='C')link(x,y);
else cut(x,y);
}
return 0;
}
练习
1
这道题目不是弹飞绵羊吗?对吧。
时间限制: 1 Sec 内存限制: 20 MB
【题意】
有n个点,一开始有n条边,点只会向比自己编号大的一个点连一条边,其中有的边(保证至少有一条,就是n到其他点)会连不到点,被hhn送往神奇的地方。
有两种操作:
op=1 , x : 询问从x点出发,需要经过多少个点(包括x)才会去到神奇的地方
op=2 ,x,k : 将x点连向其他点的边删掉,然后从x向x+k连一条边
【输入格式】
第一行为一个正整数n,表示点的个数
第二行n个数ki,表示第i个点向第i+ki个点连一条边,若i+ki>n 去往神奇的地方。
第三行为一个正整数m,表示操作的个数
以下m行,一行表示一个操作。
每行开头是一个整数op,
op=1时之后有一个整数x代表询问点的编号。
op=2时之后有两个整数x,k代表点的编号和改变连边的距离。
操作如题意。
【输出格式】
对于每个1操作,从x点出发,需要经过多少个点(包括x)才会被hhn送往神奇的地方。
【样例输入】
4
1 2 1 1
3
1 2
2 2 1
1 2
【样例输出】
2
3
【数据说明】
对于40%的数据,n,m<=10000
对于100%的数据,n<=200000,m<=100000
提示:你不是把神奇的地方当作一个点都不会吧,这样图中边数恒等于n啊, 这题和上一题差不多,就多一个求到根的距离而已~
尽管这题可以暴力求距离(强烈不推荐)但是利用伸展树c来做更加方便,也有利于理解。(引入make_tree)
一道裸的LCT吗,这么简单对吧,别忘了把弹飞设为(n+1)不就好起来了吗 (^ o ^) /~。
#include<cstdio>
#include<cstring>
#define N 410000
using namespace std;
struct node
{
int son[2],f,size;bool sv;
}tr[N];
inline void update(int x){tr[x].size=tr[tr[x].son[0]].size+tr[tr[x].son[1]].size+1;}
inline int chk(int x){return tr[tr[x].f].son[1]==x;}
inline bool nroot(int x){return tr[tr[x].f].son[0]==x || tr[tr[x].f].son[1]==x;}
inline void rotate(int x)
{
int f=tr[x].f,ff=tr[f].f,w=chk(x)^1,son=tr[x].son[w];
int r,R;
r=son;R=f;tr[r].f=R;tr[R].son[w^1]=r;
r=x;R=ff;tr[r].f=R;if(nroot(f))tr[R].son[chk(f)]=r;
r=f;R=x;tr[r].f=R;tr[R].son[w]=r;
update(f);update(x);
}
void pushdown(int x)
{
if(tr[x].sv==true)
{
tr[x].sv=0;tr[tr[x].son[0]].sv^=1;tr[tr[x].son[1]].sv^=1;
tr[x].son[0]^=tr[x].son[1]^=tr[x].son[0]^=tr[x].son[1];
}
}
int sta[N],len;
void splay(int x)
{
int y=x;sta[len=1]=y;
while(nroot(y))sta[++len]=y=tr[y].f;
while(len)pushdown(sta[len--]);
while(nroot(x))
{
int f=tr[x].f,ff=tr[f].f;
if(!nroot(f))rotate(x);
else rotate(chk(x)^chk(f)?x:f),rotate(x);
}
}
void ace(int x)
{
for(int y=0;x;x=tr[y=x].f)
{
splay(x),tr[x].son[1]=y,update(x);
}
}
int findroot(int x)
{
ace(x);splay(x);
int y=x;while(tr[y].son[0])y=tr[y].son[0],pushdown(y);
return y;
}
void makeroot(int x)
{
ace(x);splay(x);
tr[x].sv^=1;
}
void link(int x,int y)
{
makeroot(x);
tr[x].f=y;
}
void spilt(int x,int y)
{
makeroot(x);
ace(y);splay(x);
}
void cut(int x,int y)
{
spilt(x,y);
tr[x].son[1]=0;tr[y].f=0;update(x);
}
int a[N],n,m;
inline int get(int x){return x>n?n+1:x;}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
int now=get(i+a[i]);
link(i,now);
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int tt,x,y;scanf("%d%d",&tt,&x);
if(tt==1)
{
spilt(n+1,x);
printf("%d
",tr[n+1].size-1);
}
else
{
scanf("%d",&y);
int no1=get(x+a[x]),no2=get(x+y);
if(no1!=no2)cut(x,no1),link(x,no2);
a[x]=y;
}
}
return 0;
}
2
【题意】
一开始给你一棵n个点n-1条边的树,每个点有一个权值wi。
三种操作:
op=1 u v :在点u和点v之间建一条边。
op=2 u v:摧毁点u到点v之间的边。
op=3 w u v:将点u和点v之间路径上的点(包括u,v),权值增加w。
op=4 u v:询问点u到点v之间路径上的点(包括u,v),权值最大值。
当操作违法时(询问一中u,v已经连通,询问二中u,v没有直接连边或不连通,三四中u,v不连通,一二操作u==v)不进行操作并输出-1。
【输入格式】
第1行为1个正整数n,表示点的个数。
第2~n行为开始树所有的边,每行两个正整数u,v,代表u和v之间有一条边。
第n+1行有n个正整数,表示一开始点的权值。
下一行为一个正整数m代表下来有m个操作。
以下m行,一行表示一个操作。
行首先输入一个正整数op。
当op=1,2,4时,输入两个正整数u,v
当op=3时,输入三个正整数w,u,v
操作如题意
【输出格式】
对每个4操作,输出点u到点v之间路径上的点(包括u,v),权值最大值。同时对于违法情况输出-1。
【样例输入】
5
1 2
2 4
2 5
1 3
1 2 3 4 5
6
4 2 3
2 1 2
4 2 3
1 3 5
3 2 1 4
4 1 4
【样例输出】
3
-1
7
【数据说明】
100%的数据满足n, m≤300000,0<=w<=3000
所有数据不爆int
之前说过,Splay的下传我写的比较丑。
没有什么不是个spilt加上Splay不能修改的事情QMQ。
#include<cstdio>
#include<cstring>
#pragma GCC optimize("Ofast")
#define N 310000
using namespace std;
struct node
{
int son[2],f,c1/*本身的值*/,c2/*最大值*/,la/*lazy*/;bool sv;
}tr[N];
inline int chk(int x){return tr[tr[x].f].son[1]==x;}
inline void pushdown(int x)
{
if(tr[x].sv==true)
{
tr[x].son[0]^=tr[x].son[1]^=tr[x].son[0]^=tr[x].son[1];
tr[tr[x].son[0]].sv^=1;tr[tr[x].son[1]].sv^=1;tr[x].sv=0;
}
if(tr[x].la)
{
tr[x].c1+=tr[x].la;tr[x].c2+=tr[x].la;
tr[tr[x].son[0]].la+=tr[x].la;tr[tr[x].son[1]].la+=tr[x].la;tr[x].la=0;
}
}
inline int mymax(int x,int y){return x>y?x:y;}
inline void update(int x){tr[x].c2=mymax(mymax(tr[tr[x].son[0]].c2,tr[tr[x].son[1]].c2),tr[x].c1);}
inline bool nroot(int x){return tr[tr[x].f].son[0]==x || tr[tr[x].f].son[1]==x;}
inline void rotate(int x)
{
int f=tr[x].f,ff=tr[f].f,w=chk(x)^1,son=tr[x].son[w];
int r,R;
r=son;R=f;tr[r].f=R;tr[R].son[w^1]=r;
r=x;R=ff;tr[r].f=R;if(nroot(f))tr[R].son[chk(f)]=r;
r=f;R=x;tr[r].f=R;tr[R].son[w]=r;
update(f);update(x);
}
int sta[N],len;
inline void splay(int x)
{
int y=x;len=0;
if(tr[x].son[0])sta[++len]=tr[x].son[0];
if(tr[x].son[1])sta[++len]=tr[x].son[1];
sta[++len]=y;
while(nroot(y))
{
int w=chk(y)^1;y=tr[y].f;
if(tr[y].son[w])sta[++len]=tr[y].son[w];
sta[++len]=y;
}
while(len)pushdown(sta[len--]);
//就是下传的时候还要把儿子的传了,不然一个update不就崩起来了吗。
while(nroot(x))
{
int f=tr[x].f,ff=tr[f].f;
if(!nroot(f))rotate(x);
else rotate(chk(x)^chk(f)?x:f),rotate(x);
}
}
void ace(int x)
{
for(int y=0;x;x=tr[y=x].f)
{
splay(x),tr[x].son[1]=y,update(x);
}
}
void makeroot(int x)
{
ace(x);splay(x);
tr[x].sv^=1;
}
int findroot(int x)
{
ace(x);splay(x);
int y=x;while(tr[y].son[0])y=tr[y].son[0],pushdown(y);
return y;
}
void link(int x,int y)
{
makeroot(x);
if(findroot(y)!=x)tr[x].f=y;
else printf("-1
");
}
void spilt(int x,int y)
{
makeroot(x);
ace(y);splay(x);
}
void cut(int x,int y)
{
spilt(x,y);
if(tr[y].f==x && !tr[y].son[0])tr[x].son[1]=0,tr[y].f=0,update(x);
else printf("-1
");
}
int n,m;
int a[N],b[N];
int main()
{
tr[0].c2=-999999999;
scanf("%d",&n);
for(int i=1;i<n;i++)scanf("%d%d",&a[i],&b[i]);
for(int i=1;i<=n;i++){scanf("%d",&tr[i].c1);tr[i].c2=tr[i].c1;}
for(int i=1;i<n;i++)link(a[i],b[i]);
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int tt,x,y,z;scanf("%d%d%d",&tt,&x,&y);
if(tt==1)
{
if(x==y)printf("-1
");
else link(x,y);
}
else if(tt==2)
{
if(x==y)printf("-1
");
else cut(x,y);
}
else if(tt==3)
{
scanf("%d",&z);
if(findroot(z)!=findroot(y))printf("-1
");
else
{
spilt(y,z);
tr[y].la+=x;
pushdown(y);
}
}
else
{
if(findroot(x)!=findroot(y))printf("-1
");
else
{
spilt(x,y);
printf("%d
",tr[x].c2);
}
}
}
return 0;
}
3
时间限制: 2 Sec 内存限制: 30 MB
【题意】
一棵n个点的树,每个点的初始权值为1。对于这棵树有q个操作,每个操作为以下四种操作之一:
1 u v c:将u到v的路径上的点的权值都加上自然数c;
2 u v c:将u到v的路径上的点的权值都乘上自然数c;
3 u1 v1 u2 v2:摧毁点u1到点v1之间的边,加入一条新边(u2,v2),保证操作完之后仍然是一棵树;
4 u v:询问u到v的路径上的点的权值和,求出答案对于51061的余数。
【输入格式】
第一行两个整数n,q
接下来n-1行每行两个正整数u,v,描述这棵树
接下来q行,每行描述一个操作
【输出格式】
对于每个/对应的答案输出一行
【样例输入】
3 2
1 2
2 3
2 1 3 4
4 1 1
【样例输出】
4
【数据说明】
100%的数据保证,1<=n,q<=100000,0<=c<=10000
加乘不能混用?那是因为我们老想着先加再乘,但是如果我们想着先乘再加呢?每次有乘标记时先让加标记乘一乘,不就好起来了吗?说实话,我也是第一次做到标记改标记的题。
#include<cstdio>
#include<cstring>
#define N 110000
#define mod 51061
using namespace std;
typedef long long LL;
struct node
{
LL son[2],f,c,sum,size,la1,la2;bool sv;
}tr[N];
inline LL chk(LL x){return tr[tr[x].f].son[1]==x;}
inline bool nroot(LL x){return tr[tr[x].f].son[0]==x || tr[tr[x].f].son[1]==x;}
inline LL update(LL x){tr[x].sum=(tr[tr[x].son[0]].sum+tr[tr[x].son[1]].sum+tr[x].c)%mod;tr[x].size=tr[tr[x].son[0]].size+tr[tr[x].son[1]].size+1;}
inline void rotate(LL x)
{
LL f=tr[x].f,ff=tr[f].f,w=chk(x)^1,son=tr[x].son[w];
LL r,R;
r=son;R=f;tr[r].f=R;tr[R].son[w^1]=r;
r=x;R=ff;tr[r].f=R;if(nroot(f))tr[R].son[chk(f)]=r;
r=f;R=x;tr[r].f=R;tr[R].son[w]=r;
update(f);update(x);
}
//先乘后加
inline void jia(LL x,LL d){tr[x].la1+=d;tr[x].la1%=mod;}
inline void cheng(LL x,LL d){tr[x].la1*=d;tr[x].la2*=d;tr[x].la1%=mod;tr[x].la2%=mod;}
void pushdown(LL x)
{
if(tr[x].sv)
{
tr[x].sv=0;
tr[x].son[0]^=tr[x].son[1]^=tr[x].son[0]^=tr[x].son[1];
tr[tr[x].son[0]].sv^=1;tr[tr[x].son[1]].sv^=1;
}
if(tr[x].la2!=1)
{
tr[x].sum*=tr[x].la2;tr[x].c*=tr[x].la2;tr[x].sum%=mod;tr[x].c%=mod;
cheng(tr[x].son[0],tr[x].la2);cheng(tr[x].son[1],tr[x].la2);
tr[x].la2=1;
}
if(tr[x].la1)
{
tr[x].sum+=tr[x].la1*tr[x].size;tr[x].c+=tr[x].la1;
tr[x].sum%=mod;tr[x].c%=mod;
jia(tr[x].son[0],tr[x].la1);jia(tr[x].son[1],tr[x].la1);
tr[x].la1=0;
}
}
LL sta[N],len;
inline void splay(LL x)
{
LL y=x;len=0;
if(tr[x].son[0])sta[++len]=tr[x].son[0];
if(tr[x].son[1])sta[++len]=tr[x].son[1];
sta[++len]=x;
while(nroot(y))
{
LL w=chk(y)^1;y=tr[y].f;
if(tr[y].son[w])sta[++len]=tr[y].son[w];
sta[++len]=y;
}
while(len)pushdown(sta[len--]);
while(nroot(x))
{
LL f=tr[x].f,ff=tr[f].f;
if(!nroot(f))rotate(x);
else rotate(chk(x)^chk(f)?x:f),rotate(x);
}
}
inline void ace(LL x)
{
for(LL y=0;x;x=tr[y=x].f)splay(x),tr[x].son[1]=y,update(x);
}
inline LL findroot(LL x)
{
ace(x);splay(x);
LL y=x;while(tr[y].son[0])y=tr[y].son[0],pushdown(y);
return y;
}
inline void makeroot(LL x)
{
ace(x);splay(x);
tr[x].sv^=1;
}
inline void link(LL x,LL y)
{
makeroot(x);tr[x].f=y;
}
inline void spilt(LL x,LL y)
{
makeroot(x);
ace(y);splay(x);
}
inline void cut(LL x,LL y)
{
spilt(x,y);
tr[x].son[1]=0;tr[y].f=0;update(x);
}
LL n,m;
int main()
{
scanf("%lld%lld",&n,&m);
for(LL i=1;i<=n;i++)tr[i].c=tr[i].sum=1,tr[i].la2=1,tr[i].size=1;
for(LL i=1;i<n;i++)
{
LL x,y;scanf("%lld%lld",&x,&y);
link(x,y);
}
for(LL i=1;i<=m;i++)
{
LL tt,x,y;scanf("%lld%lld%lld",&tt,&x,&y);
if(tt==1)
{
LL c;scanf("%lld",&c);
spilt(x,y);
jia(x,c);
}
else if(tt==2)
{
LL c;scanf("%lld",&c);
spilt(x,y);
cheng(x,c);
}
else if(tt==3)
{
cut(x,y);scanf("%lld%lld",&x,&y);
link(x,y);
}
else
{
spilt(x,y);
printf("%lld
",tr[x].sum);
}
}
return 0;
}
小结
为什么说未完待续,因为还有Qtree呢。