题目链接:
Fire-Control System
Time Limit: 12000/5000 MS (Java/Others)
Memory Limit: 32768/32768 K (Java/Others)
Problem Description
A new mighty weapon has just been developed, which is so powerful that it can attack a sector of indefinite size, as long as the center of the circle containing the sector is the location of the weapon. We are interested in developing a fire-control system that calculates firing-solutions automatically.
The following example gives an example of a firing solution:
Figure 1
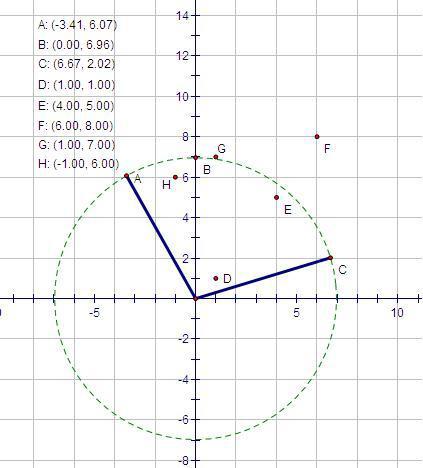
Here the firing region is the sector "ABC" that covers six points: A, B, C, D, E, H. You may further assume that the weapon is always located at point (0, 0), no targets will be on the point (0, 0) and the coordinates of the targets will be distinct.
A firing solution is called effective if and only if it covers a minimum of K points
out of N given points (targets) on the two-dimensional Cartesian plane. Furthermore,since the cost of a particular fire solution is in direct proportion to the size of the area it covers, a firing could be quite costly; thus we are only interested in the optimal firing solution with the minimum cost.
The following example gives an example of a firing solution:
Figure 1

Here the firing region is the sector "ABC" that covers six points: A, B, C, D, E, H. You may further assume that the weapon is always located at point (0, 0), no targets will be on the point (0, 0) and the coordinates of the targets will be distinct.
A firing solution is called effective if and only if it covers a minimum of K points
out of N given points (targets) on the two-dimensional Cartesian plane. Furthermore,since the cost of a particular fire solution is in direct proportion to the size of the area it covers, a firing could be quite costly; thus we are only interested in the optimal firing solution with the minimum cost.
Input
There are multiple test cases in the input file.
Each test case starts with two non-negative integers, N and K
(1 ≤ N ≤ 5000 , K ≤ N ), followed by N lines each containing two integers, X, and Y, describing the distinct location of one target. It is guaranteed that the absolute value of any integer does not exceed 1000.
Two successive test cases are separated by a blank line. A case with N = 0 and K = 0 indicates the end of the input file, and should not be processed by your program.
Each test case starts with two non-negative integers, N and K
(1 ≤ N ≤ 5000 , K ≤ N ), followed by N lines each containing two integers, X, and Y, describing the distinct location of one target. It is guaranteed that the absolute value of any integer does not exceed 1000.
Two successive test cases are separated by a blank line. A case with N = 0 and K = 0 indicates the end of the input file, and should not be processed by your program.
Output
For each test case, please print the required size (to two decimal places), in the
format as indicated in the sample output.
format as indicated in the sample output.
Sample Input
3 1
0 1
1 0
-5 -6
3 2
0 2
2 0
-5 -6
0 0
Sample Output
Case #1: 0.00
Case #2: 3.14
题意:
给n个点,找出一个圆心在(0,0)的扇形,至少覆盖k个点,使得扇形的面积最小;
思路:
枚举半径r,找到与原点距离小于等于r的点,这些点极角排序后看覆盖k个点的面积,更新最小值就可以,在k==0的地方wa了几发;
AC代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
template<class T> void read(T&num) {
char CH; bool F=false;
for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
if(!p) { puts("0"); return; }
while(p) stk[++ tp] = p%10, p/=10;
while(tp) putchar(stk[tp--] + '0');
putchar('
');
}
const LL mod=998244353;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e4+10;
const int maxn=1e3+10;
const double eps=1e-4;
struct node
{
int x,y;
double dis,ang;
}po[N];
int temp[N];
int cmp(node a,node b)
{
if(a.ang<b.ang)return 1;
return 0;
}
int main()
{
int Case=0;
while(1)
{
int n,k;
read(n);read(k);
if(!n&&!k)break;
printf("Case #%d: ",++Case);
For(i,1,n)
{
read(po[i].x),read(po[i].y);
po[i].ang=atan2(po[i].y,po[i].x);
po[i].dis=sqrt(po[i].x*po[i].x+po[i].y*po[i].y);
}
sort(po+1,po+n+1,cmp);
For(i,1,n)
{
po[i+n]=po[i];
po[i+n].ang+=2*PI;
}
double ans=1e18;
if(k==0)ans=0;
For(i,1,n)
{
double r=po[i].dis;
int cnt=0;
For(j,1,2*n)if(po[j].dis<=po[i].dis+eps)temp[++cnt]=j;
For(j,1,cnt)
{
if(temp[j]>n||j+k-1>cnt||temp[j+k-1]-temp[j]>=n)continue;
double angle=po[temp[j+k-1]].ang-po[temp[j]].ang;
ans=min(ans,angle*r*r/2);
}
}
printf("%.2lf
",ans);
}
return 0;
}