1 #include<bits/stdc++.h>
2 using namespace std;
3 int main()
4 {
5 int T;
6 scanf("%d",&T);
7 while(T--)
8 {
9 int n,a,b,c;
10 scanf("%d",&n);
11 scanf("%d%d%d",&a,&b,&c);
12 int sum=n/a+n/b+n/c-2*(n/a/b+n/a/c+n/b/c)+4*(n/a/b/c);//因为a,b,c都为质数所以直接相除即可,若不是质数,应该乘上最大公约数
13 printf("%d
",sum);
14 }
15 return 0;
16 }
电灯泡
TimeLimit:1000MS MemoryLimit:128MB
64-bit integer IO format:%lld
未提交 | 登录后收藏 | 已有6人收藏了本题
Problem Description
V_Dragon有n栈电灯泡,编号为1-n,每个灯泡都有一个开关。那么问题来了
-
所有灯泡初始时为不亮的
-
V_Dragon分别进行三次操作
-
每次操作他都选一个质数x,将编号为x和x的整数倍的灯泡的开关都拨动一下(如果灯为亮,那么拨动以后灯为不亮,如果灯不亮,拨动以后变为亮)
求最后亮着的灯的数量
Input
输入T表示T组测试数据(1<=T<=100)
接下来T组测试数据
每组第一行一个n表示灯泡个数(1<=n<=10^9)
第二行三个数a,b,c表示V_Dragon每次选择的数(1<=a,b,c<=10^6)(a,b,c全为质数且a,b,c两两互不相等)
不懂格式的同学可以参考以下格式:
Output
数组最后亮着的灯的个数
SampleInput
15
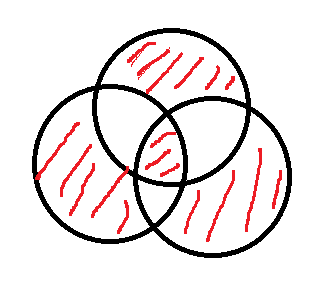
画一下图可以知道最后亮着的灯泡的数量如下图所示
将集合A表示为被a整除的数,集合B为被b整除的数,集合C为被c整除的数。
阴影部分的面积求法:S-AB-AC-BC+3ABC
而S=A+B+C-AB-AC-BC+ABC 整理得阴影部分面积为A+B+C-2*(AB+AC+BC)+4*ABC