任国庆 张博
之前我们讨论了在一维数组中求最大子数组的和,在此基础上我们开始讨论二维数组的最大子数组。
求二维数组的最大子数组思想是建立在以为数组。首先将数组的第一列看成一个一维数组,找到该列的最大子数组的值,然后将第二列与第一列看成是一个新一列,这样就又出现了一个新的一维数组,重复以上的步骤,就可以全部搜索二维数组,找到其中最大子数组的值。
#include "stdafx.h" int main() { int m,n,i,j,k,z; static int q=0,b; printf("请输入数组的行数和列数 "); scanf("%d%d",&q,&b); int sum1,sum[100]; int a[100][100]; int max=0; printf("请输入数据 "); for(i=0;i<q;i++) { for(j=0;j<q;j++) { scanf("%d",&a[i][j]); } } for(m=0;m<q;m++) { for(k=0;k<q;k++) { sum[k]=0; } //初始化 for(j=m;j<q;j++) { for(i=0;i<q;i++) { sum[i]+=a[i][j]; } //求行的值变成一维数 for(n=0;n<q;n++) { sum1=0; for(z=n;z<q;z++) { sum1+=sum[z]; if(sum1>max) { max=sum1; } } } } } printf("最大值为%d ",max); return 0; }
一下是我们组讨论的图
实验结果
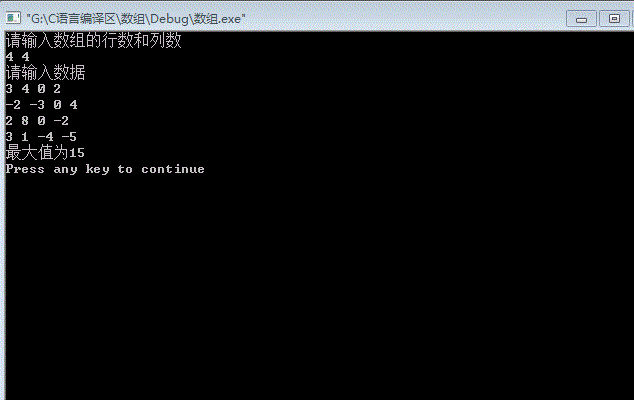
实验猜想
基于以上的讨论我们组找到了二维数组中最大子数组的值,但是这方法比较笨,时间复杂度是O(n*3).所以我们猜想应该找到一个算法,以数组中最大值为一点,进行扩散的寻找最大子数组的值,这样程序执行起来时间复杂度会降低,因此我们组将继续讨论,以降低时间复杂度.