本系列为《数据结构》(严蔚敏48集视频)学习笔记,温故而知新,IT从业者,夯实基础,书常读常新!
本章学习要点
1)熟悉各名词、术语的含义,掌握基本概念;
2)理解算法五个要素的确切含义;
3)掌握计算语句频度和估算算法时间复杂度的方法。
1,数据结构讨论的范畴
1)程序设计=算法+数据结构
程序设计:为计算机处理问题编制一组指令集;
算法:处理问题的策略;
数据结构:问题的模型。
数值计算的问题:
例如:结构静力分析计算---------线性代数方程组;全球天气预报------------环流模式方程。
非数值计算的问题:
例1:求一组整数(n)中的最大值。
例2:计算机对弈。
例3:足协的数据库管理。
小结:数据结构描述现实世界实体的数学模型(非数值计算)及其上的操作在计算机中的表示和实现。
2,基本概念
1)数据和数据结构
数据:所有能被输入到计算机中,且被计算机处理的符号的集合计算机操作的对象的总称,是计算机处理的信息的某种特定的符号表示形式。
数据元素:数据中的一个“个体”,数据结构中讨论的基本单位。
数据项:数据结构中讨论的最小单位,数据元素是数据项的集合。
数据结构:带结构的数据元素的集合。
数据的逻辑结构:线性结构,树形结构,图状结构,集合结构。
数据结构的形式定义:
数据结构是一个二元组Data_Structures=(D,S)。其中D是数据元素的有限集,S是D上关系的有限集。
数据结构存储结构:逻辑结构在存储器中的映像。
数据元素的映象方法:用二进制位(bit)的位串表示数据元素;
关系的映象方法:(表示<x,y>的方法)
顺序映象:以存储位置的相邻表示后继关系;
链式映象:以附加信息(指针)表示后继关系。
2)数据类型
数据类型是一个值的集合和定义在此集合上的一组操作的总称。
3)抽象数据类型
抽象数据类型(Abstract Data Type 简称ADT)是指一个数学模型以及定义在此数学模型上的一组操作。
ADT两大重要特征:
数据抽象:用ADT描述程序处理的实体时,强调的是其本质的特征,其所能完成的功能以及它和外部用户的接口;
数据封装:将实体的外部特性和其内部实现细节分离,并且对外部用户隐藏其内部实现细节。
ADT描述方法:(D,S,P)
其中:D是数据对象;S是D上的关系集;P是对D的基本操作集。
ADT的表示和实现:ADT需要通过固有数据类型(高级编程语言中已经实现的数据类型)来实现。
3,算法和算法衡量
1)算法
算法是为了解决某类问题而规定的一个有限长的操作序列。一个算法必须满足以下五个重要特性:
(1)有穷性:算法中每个步骤都能在有限时间内完成;
(2)确定性:对于每种情况下所应执行的操作,在算法中都有确切的规定,且在任何条件下,算法都只有一条执行路径;
(3)可行性:算法中的所有操作都必须足够基本;
(4)有输入:作为算法加工对象的量值,通常体现为算法中的一组变量;
(5)有输出。
2)算法设计原则
(1)正确性:算法应当满足以特定的“规格说明”方式给出的需求;对“正确”的理解:a,b,c,d;
(2)可读性:算法应该易于人的理解;
(3)健壮性:当输入的数据非法时,算法应当恰当地作出反应或进行相应的处理;
(4)高效率与低存储量需求:效率指算法执行时间,存储量指算法执行过程中所需的最大存储空间。二者都与问题的规模有关。
3)算法效率的衡量方法和原则
(1)事后统计法:必须执行程序;其他因素掩盖算法本质。
(2)事前分析估算法
和算法执行时间相关的因素:算法选用的策略;问题的规模;编程程序的语言;编译程序产生的机器代码的质量;计算机执行指令的速度。
随着问题规模n的增长,算法执行时间的增长率和f(n)的增长率相同。则可记作:T(n)=O(f(n)),称T(n)为算法的(渐近)时间复杂度。
算法=控制结构+原操作(固有数据类型的操作)
算法的执行时间 = ∑原操作(i)的执行次数×Σ原操作(i)的执行时间
从算法中选取一种对于所研究的问题来说是基本操作的原操作,以该基本操作在算法中重复执行的次数作为算法运行时间的衡量准则。
例题1:
1 for(i = 1; i <= n; i++) 2 for (j = 0; j <=n; j++) 3 { 4 c[i,j]=0; 5 for (k = 0; k <= n; k++) 6 c[i,j] += a[i,k]*b[k,j]; 7 }
例题2:
1 void select_sort(int a[], int n) 2 { 3 //将a中整数序列重新排列成自小到大有序的整数序列 4 for (int i = 0; i < n-1; ++i) 5 { 6 j = i; 7 for (int k = i+1; k < n; ++k) 8 { 9 if (a[k] < a[j]) 10 j = k; 11 if (j != i) a[j] <--> a[i] 12 } 13 } 14 }
例题3:
1 void bubble_sort(int a[], int n) 2 { 3 //将a中整数序列重新排列成自小到大有序的整数序列 4 for (int i = n-1, change = TRUE; i > 1 && change; --i) 5 { 6 change = FALSE; 7 for (int j = 0; j < i; ++j) 8 { 9 if (a[j] > a[j+1]) 10 {a[j] <--> a[j+1]; 11 change = TRUE;} 12 } 13 } 14 }
4)算法的存储空间需求
算法的空间复杂度:S(n)=O(g(n)),表示随着问题规模n的增长,算法运行所需存储量的增长率与g(n)的增长率相同。
算法的存储量包括:输入数据所占空间;程序本身所占空间;辅助变量所占空间。
若所需额外空间相对于输入数据量来说是常数,则称此算法为原地操作。
附录:代码实现清单
partOne.cpp

1 #include<stdlib.h> 2 #include "structure.h" 3 4 #include <iostream> 5 using namespace std; 6 7 8 //矩阵乘法 9 int** matrixMultiplcate(int** a, int** b, int n) 10 { 11 int** c; 12 c = (int **)malloc(sizeof(int *)*n); 13 for(int m = 0; m < n; m++) 14 c[m] = (int *)malloc(sizeof(int)*n); 15 16 for (int i = 0; i < n; ++i) 17 for (int j = 0; j < n; ++j) 18 { 19 c[i][j] = 0; 20 for ( int k = 0; k < n; ++k) 21 c[i][j] += a[i][k] * b[k][j]; 22 } 23 return c; 24 } 25 26 27 void dispalayMatrix() 28 { 29 int a[5][5] = {{1, 2}, {3, 4, 5}, {6}, {7}, {0, 8}}; 30 int b[5][5] = {{1, 2}, {3, 4, 5}, {6}, {7}, {0, 8}}; 31 int **p; 32 int i, j, n = 5; 33 34 p = (int **)malloc(sizeof(int *)*n); 35 for(int m = 0; m < n; m++) 36 p[m] = (int *)malloc(sizeof(int)*n); 37 38 cout <<"原矩阵:"<< endl; 39 for (i = 0; i < n; ++i) 40 { 41 for (j = 0; j < n; ++j) 42 { 43 p[i][j] = a[i][j]; 44 cout << a[i][j] << " " ; 45 } 46 cout << endl; 47 } 48 cout << endl; 49 50 int **c = matrixMultiplcate(p,p,n); 51 cout <<"新矩阵:"<< endl; 52 for (i = 0; i < n; ++i) 53 { 54 for (j = 0; j < n; ++j) 55 cout << c[i][j] << " " ; 56 cout << endl; 57 } 58 } 59 60 61 //选择排序 62 int* select_sort(int a[], int n) 63 { 64 //将a中整数序列重新排列成自小到大有序的整数序列 65 int j, temp = 0; 66 for (int i = 0; i < n-1; ++i) 67 { 68 j = i; 69 for (int k = i+1; k < n; ++k) 70 { 71 if (a[k] < a[j]) 72 j = k; 73 if (j != i) 74 { 75 temp = a[j]; 76 a[j] = a[i]; 77 a[i] = temp; 78 } 79 } 80 } 81 return a; 82 } 83 84 85 void display_select_sort() 86 { 87 int a[10]; 88 int i = 0; 89 for (i = 10; i>0; i--) 90 a[10-i] = i; 91 92 cout << "原始数组:" << endl; 93 for (i = 0; i < 10; i++) 94 cout << a[i] << " "; 95 96 int* new_a = select_sort(a, 10); 97 cout << "选择排序后数组:" << endl; 98 for (i=0; i<10; i++) 99 cout << new_a[i] << " "; 100 } 101 102 103 //冒泡排序 104 int* bubble_sort(int a[], int n) 105 { 106 //将a中整数序列重新排列成自小到大有序的整数序列 107 bool change = true; 108 int temp = 0; 109 for (int i = n-1; i > 0 && change; --i) 110 { 111 change = false; 112 for (int j = 0; j < i; ++j) 113 { 114 if (a[j] > a[j+1]) 115 { 116 temp = a[j]; 117 a[j] = a[j+1]; 118 a[j+1] = temp; 119 change = true; 120 } 121 } 122 } 123 return a; 124 } 125 126 127 void display_bubble_sort() 128 { 129 int a[10]; 130 int i = 0; 131 for (i = 10; i>0; i--) 132 a[10-i] = i; 133 134 cout << "原始数组:" << endl; 135 for (i = 0; i < 10; i++) 136 cout << a[i] << " "; 137 138 int* new_a = bubble_sort(a, 10); 139 cout << "冒泡排序后数组:" << endl; 140 for (i=0; i<10; i++) 141 cout << new_a[i] << " "; 142 }
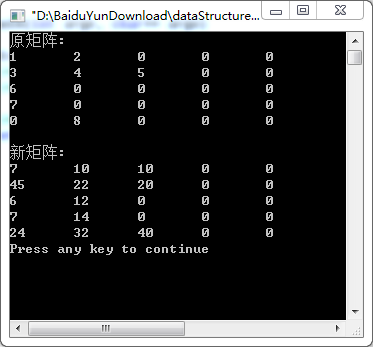
运行结果如下: