一、通过Floyd 算法 算出两点间最短路径并进行输出
现已知一个复杂的地铁线路图如下:
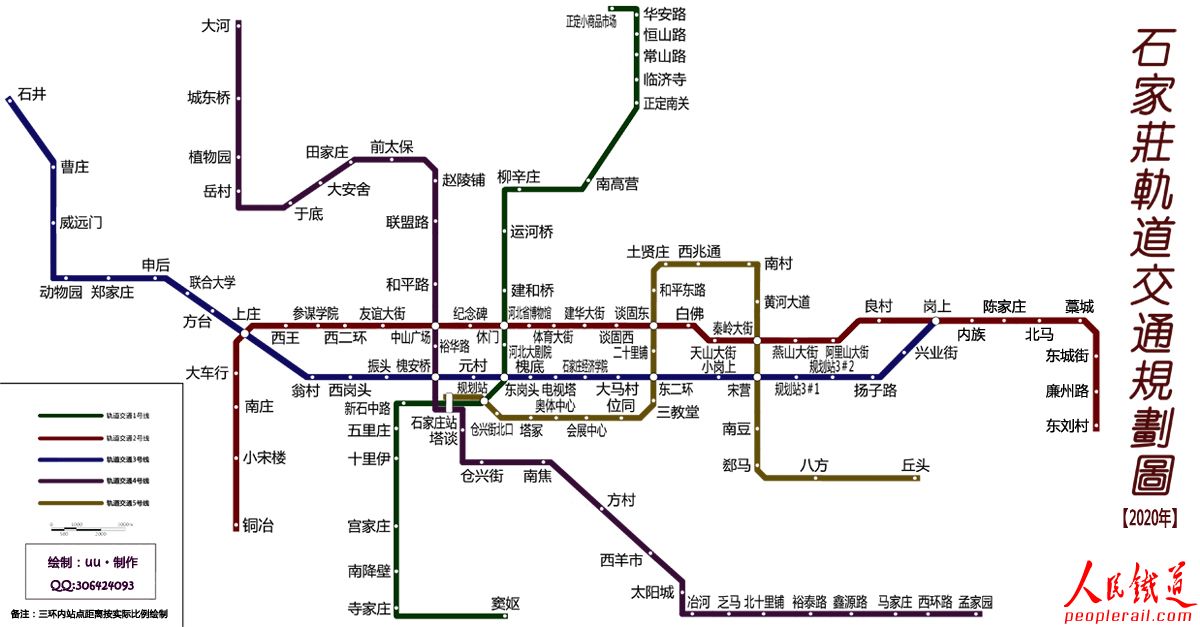
要想知道图中任意两点之间的 最短路径 可以采用Floyd算法 解决步骤如下:
1、将各个节点 存放到一个数组中(可以手动输入,当然可以从数据库中取)
1 public String[] siteName= new String[]{ 2 /*1号线:石井——兴业街*/ 3 /*1-10*/ 4 "石井","曹庄","威远门","动物园","郑家庄","申后","联合大学","方台","翁村","西岗头", 5 /*11-20*/ 6 "振头","元村","槐底","电视塔","石家庄经济学院","大马村","小岗上","规划站3#1","规划站3#2","扬子路", 7 /*21*/ 8 "兴业街", 9 10 /*2号线:铜冶--东刘村*/ 11 /*22-31*/ 12 "铜冶","小宋楼","南庄","大车行","西王","参谋学院","西二环","友谊大街","纪念碑","河北省博物馆", 13 /*32-41*/ 14 "体育大街","建华大街","谈固西","白佛","天山大街","燕山大街","阿里山大街","良村","内族","陈家庄", 15 /*42-46*/ 16 "北马","藁城","东城街","廉州路","东刘村", 17 18 /*3号线:正定小商品市场--窦妪*/ 19 /*47-51*/ 20 "正定小商品市场","华安路","恒山路","常山路","临济寺", 21 /*52-61*/ 22 "正定南关","南高营","柳辛庄","运河桥","建和路","河北大剧院","新石中路","五里庄","十里伊","宫家庄", 23 /*62-64*/ 24 "南降壁","寺家庄","窦妪", 25 26 /*4号线:大河--孟家园*/ 27 /*65-71*/ 28 "大河","城东桥","植物园","岳村","于底","大安舍","田家庄", 29 /*72-81*/ 30 "前太保","赵陵铺","联盟路","和平路","裕华路","塔谈","仓兴街","南焦","方村","西羊市", 31 /*82-90*/ 32 "太阳城","冶河","乏马","北十里铺","裕泰路","鑫源路","马家庄","西环路","孟家园", 33 34 /*5号线:石家庄站--丘头*/ 35 /*91*/ 36 "仓兴街北口", 37 /*92-101*/ 38 "塔冢","奥体中心","会展中心","位同","三教堂","二十里铺","和平东路","土贤庄","西兆通","南村", 39 /*102-106*/ 40 "黄河大道","南豆","希马","八方","丘头", 41 42 /*换乘点 由1-2,1-3,。。。方式输入*/ 43 /*107-112,1-。。*/ 44 "上庄","岗上","东岗头","槐安桥","东二环","宋营", 45 46 /*113-116,2-。。*/ 47 "休门","中山广场","谈固东","秦岭大街", 48 49 /*117-118,3-。。*/ 50 "石家庄站","规划站" 51 };
2、初始化一个 代表各个节点是否连接的邻接矩阵(自身采用0,其他的设为inf无穷远)
1 //初始化连接矩阵 2 for(int i=0;i<stanum;i++) 3 { 4 for(int j=0;j<stanum;j++) 5 { 6 if(i==j) 7 distance[i][j]=0; 8 else 9 distance[i][j]=inf; 10 } 11 }
3、结合实际给邻接矩阵赋值(在这里我将有连接关系的设置为1因为是地铁,当然其他的问题可以根据具体情况赋给相应的距离值)
这里还涉及到一个赋值的技巧,即将每条线路的各个节点在总的数组中的位置分别赋给代表这个线路的子数组中 然后根据相邻为1 不相邻为0的规则赋值,如果该图过于复杂可参考华为机试地铁线路问题,那个只有两条线,比较好分析。
以第一条线为例:
1 //初始化技巧 2 int s1[]={0,1,2,3,4,5,6,7,106,8,9,10,109,11,108,12,13,14,15,110,16,111,17,18,19,20,107}; 3 for( int i=0;i<s1.length-1;i++) 4 { 5 distance[s1[i]][s1[i+1]]=1; 6 distance[s1[i+1]][s1[i]]=1; 7 }
4、通过Floyd 找最短路径
1 void floyd(int dis[][],int path[][]) 2 { 3 //初始化path矩阵 4 for(int row=0;row<stanum;row++) 5 for(int col=0;col<stanum;col++) 6 path[row][col]=row; 7 8 //找最短路径 9 for(int k=0;k<stanum;k++) 10 for(int i=0;i<stanum;i++) 11 for(int j=0;j<stanum;j++) 12 if(dis[i][j]>dis[i][k]+dis[k][j]) 13 { 14 dis[i][j]=dis[i][k]+dis[k][j]; 15 path[i][j]=path[k][j]; 16 } 17 18 }
5、上一步是将所有可能的出发点到所有可能的终点的所有最短路径都找出来了,之后就要在这之中进行筛选,选出自己需要的,在这之前要先将需要的起点和终点转换成矩阵的索引
1 //转换车站的名字到矩阵的索引 2 int string2int(String s) 3 { 4 for(int i=0;i<stanum;i++) { 5 if(s.equals(site[i])) 6 { 7 return i; 8 9 } 10 } 11 return 0; 12 }
6、然后输出需要的最短路径,将路径,距离等需要的条件,封装到一个list中
1 ArrayList<Object> printres(int dis[][], int path[][], String start, String dest) 2 { 3 int s; 4 int d; 5 ArrayList<Object> arrayList=new ArrayList<Object>(); 6 s=string2int(start); 7 System.out.println("s:"+s); 8 d=string2int(dest); 9 System.out.println("d:"+d); 10 System.out.println("最少经过的车站数量: "+(dis[s][d]+1)); 11 int sumSite=dis[s][d]; 12 System.out.println("经过的车站路径编号: "); 13 String line=""; 14 15 for(int i=0;i<stanum;i++) 16 for(int j=0;j<stanum;j++) 17 { 18 if(i==s&&j==d) //输出路径 19 { 20 Stack<Integer>pathrout=new Stack<>();//压栈 21 int k=j; 22 do{ 23 k=path[i][k]; 24 Integer temp_k=new Integer(k); 25 pathrout.push(temp_k.intValue()); 26 27 }while(k!=i); 28 29 //弹栈 30 System.out.print(site[pathrout.peek()]); 31 line+=site[pathrout.peek()]; 32 pathrout.pop(); 33 34 int length=pathrout.size(); 35 for(int t=0;t<length;t++) { 36 System.out.print("->" + site[pathrout.peek()]); 37 line += "->" + site[pathrout.peek()]; 38 pathrout.pop(); 39 40 } 41 System.out.println("->"+site[d]); 42 line+="->"+site[d]; 43 break; 44 } 45 } 46 arrayList.add(line); 47 arrayList.add(sumSite); 48 return arrayList; 49 }
最后看一下效果图:
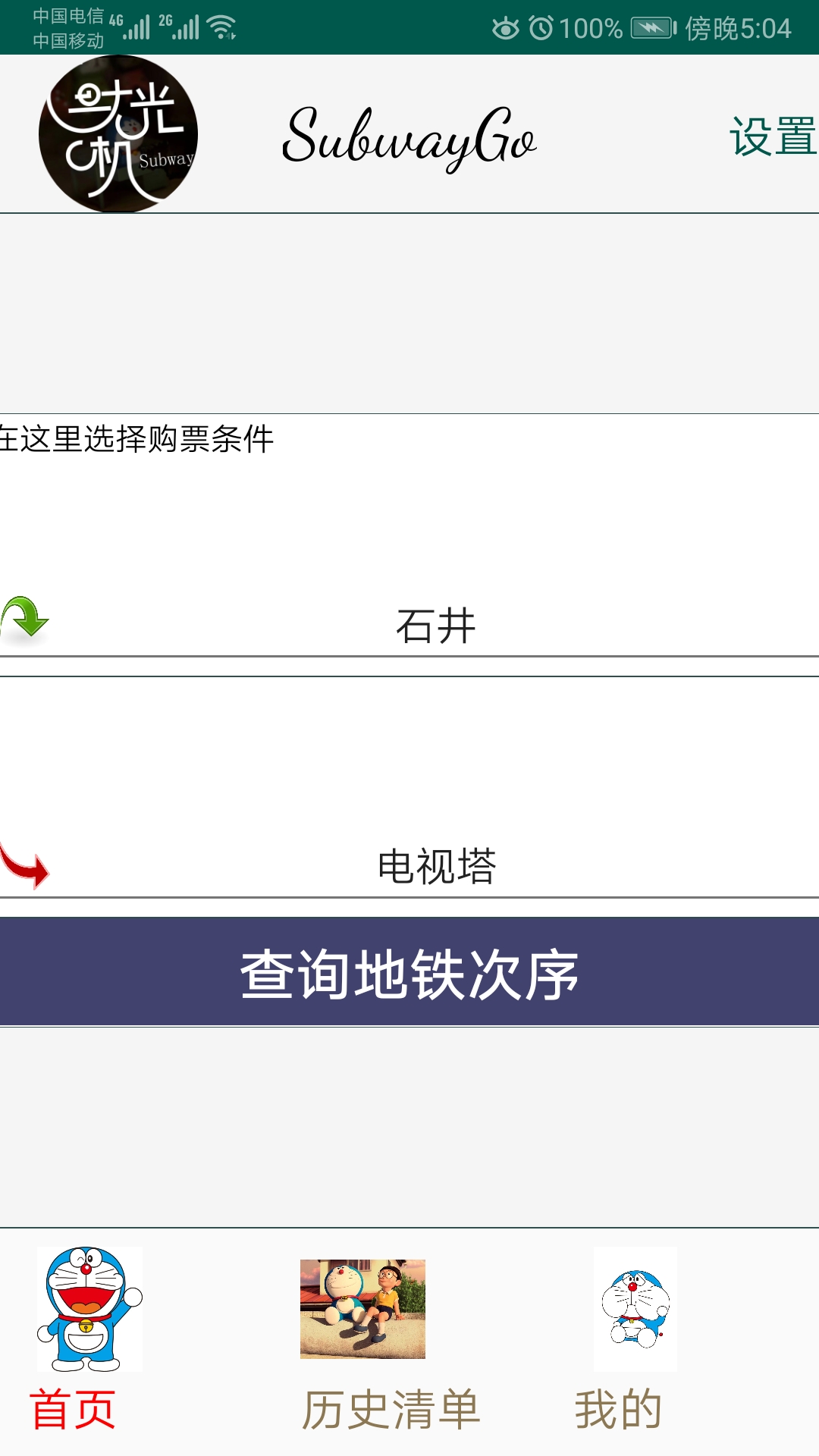 ,
, 。
。
二、总结一下,就是一个Floyd 的算法应用,其实具体细节处理还不是很好,因为用户体验感不是很好,具体转换程节点也没有明确表示出来,很有待改进,然后下一篇博客就是生成与微信或者支付宝关联的二维码(同时构建--我的页面)