首先,对于给定二叉树遍历序列,如果只有前序遍历、后序遍历、中序遍历的任意一个,无法唯一确定一棵二叉树。举个反例,如果给定二叉树前序序列AB,则该二叉树可以以A为根,B为左子树,也可以以A为根,B为右子树。这两棵树的前序遍历序列都为AB,如图1所示。
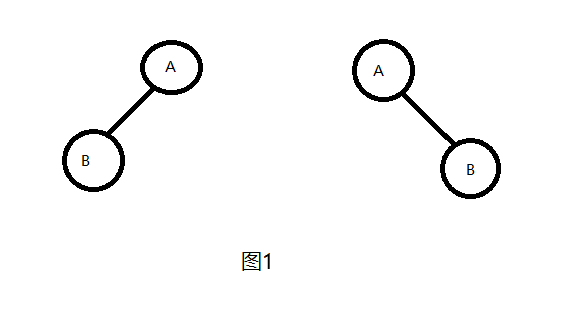
同样的,只给定后序序列也无法唯一确定一棵二叉树。对于图1的两棵树,它们的后序序列都为BA。而如果只给定中序序列呢?同样不行,如图2所示,这两棵树的中序遍历序列都是BA。
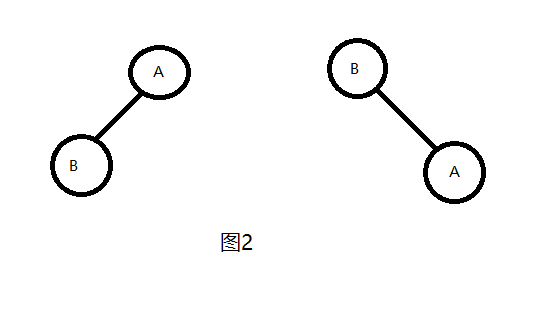
那么给定哪些遍历序列可以唯一确定一棵二叉树呢?答案是,前序遍历和中序遍历或者后序遍历和中序遍历。总之要有一个中序遍历的信息。如果只给定前序遍历和后序遍历同样无法唯一确定一棵二叉树。还是以图1为例,这两棵二叉树的前序遍历和后序遍历序列都一样。前序为AB,后序为BA。那么如何通过前序遍历和中序遍历序列或者后序遍历和中序遍历序列构建一棵二叉树呢?下面以后序遍历和中序遍历序列为例,说明一下构建流程。
如果给定中序遍历序列为CBEDAHGIJF,后序遍历序列为CEDBHJIGFA。则由后序遍历的规则可知,最后一个输出的值为根节点的值,则该二叉树的树根值为‘A’。那么再由中序遍历规则可知,在根节点前输出的为左子树序列,在根节点后输出的为右子树序列。则‘CBED’为该棵树的左子树节点序列,‘HGIJF’为该棵树的右子树节点序列。那么,再由后序遍历‘CEDB’序列可知,左子树的根节点为‘B’。然后再由中序遍历可知左子树的左子树序列为‘C’,左子树的右子树序列为‘ED’。如此递归下去,即可还原该棵二叉树,最后结果如图3所示。
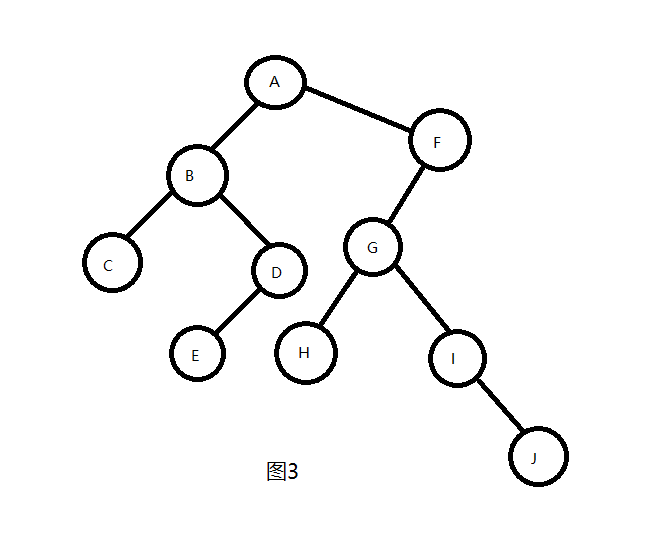
实际上二叉树的定义可以由递归方式给出,所以它的很多操作都可以由递归来实现。下面给出由后序序列和中序序列构建对应二叉树的代码。
1 //给出一棵二叉树的中序遍历和后序遍历序列还原该二叉树 2 //中序序列CBEDAHGIJF 3 //后序序列CEDBHJIGFA 4 5 #include <stdio.h> 6 #include <stdlib.h> 7 typedef int ElementType; 8 typedef struct TreeNode* PtrNode; 9 typedef PtrNode Tree; 10 struct TreeNode { 11 ElementType data; 12 Tree left; 13 Tree right; 14 }; 15 16 PtrNode createTreeNode(char data) { 17 PtrNode node = malloc(sizeof(struct TreeNode)); 18 if (!node) return NULL; 19 node->data = data; 20 node->left = NULL; 21 node->right = NULL; 22 return node; 23 } 24 25 26 Tree recoveryTree(const char* inOrderStr, const char* postOrderStr) { 27 const char* p = inOrderStr; //中序遍历字符串 28 const char* q = postOrderStr; //后序遍历字符串 29 Tree root; 30 int i = 0, j = 0; 31 int m, n; 32 if (!(*p) && !(*q)) { //如果中序遍历字符串和后序遍历字符串都为空则返回NULL 33 return NULL; 34 } 35 while (q[i]) { //遍历后序字符串,找到最后一个节点 36 j = i; 37 i++; 38 } 39 char rootData = q[j]; //使用最后节点构建树根 40 root = createTreeNode(rootData); 41 for (m = 0, n = 0; p[m] && q[n]; m++, n++) { //在中序序列中定位根节点 42 if (p[m] == rootData) 43 break; 44 } 45 char subStr1[20], subStr2[20], subStr3[20]; //在中序序列中拷贝左子树节点 46 for (m = 0; m < n; m++) { 47 subStr1[m] = p[m]; 48 } 49 subStr1[m] = '�'; 50 for (m = 0; m < n; m++) { //在后序序列中拷贝左子树节点 51 subStr2[m] = q[m]; 52 } 53 subStr2[m] = '�'; 54 55 for (i = 0, m = n; m < j; i++, m++) { //在后序序列中拷贝右子树节点 56 subStr3[i] = q[m]; 57 } 58 subStr3[i] = '�'; 59 60 root->left = recoveryTree(subStr1, subStr2); //递归构建左子树和右子树 61 root->right = recoveryTree(&p[n + 1], subStr3); //中序序列的右子树可由之前的定位根节点信息获得 62 return root; //返回构建的树 63 } 64 65 //后序遍历 66 void postOrderTraversal(Tree t) { 67 if (t) { 68 postOrderTraversal(t->left); 69 postOrderTraversal(t->right); 70 printf("%c ", t->data); 71 } 72 } 73 74 //中序遍历 75 void inOrderTraversal(Tree t) { 76 if (t) { 77 inOrderTraversal(t->left); 78 printf("%c ", t->data); 79 inOrderTraversal(t->right); 80 } 81 } 82 83 84 int main(void) { 85 char* inOrderStr = "CBEDAHGIJF"; 86 char* postOrderStr = "CEDBHJIGFA"; 87 Tree tree = recoveryTree(inOrderStr, postOrderStr); 88 postOrderTraversal(tree); 89 printf(" "); 90 inOrderTraversal(tree); 91 return 0; 92 }
代码只假定了中序序列和后序序列对应的是同一个棵二叉树未做特殊处理。由于C的标准字符串是以‘�‘结尾,所以在构建过程中需要将子字符串拷贝出并添加‘�’。