进制转换

今天学习了进制转换，整理资料如下

十进制：10个基数：0~9

二进制：2个基数：0,1

八进制：10个基数：0~7

十六进制：16个基数：0~9，A（10），B（11），C（12），D（13），E（14），F（15）

进制转化关系图，如下图

十进制——二进制

十进制数除以2，除至0时所得余数按反方向写出，即为二进制数；

例97的二进制数

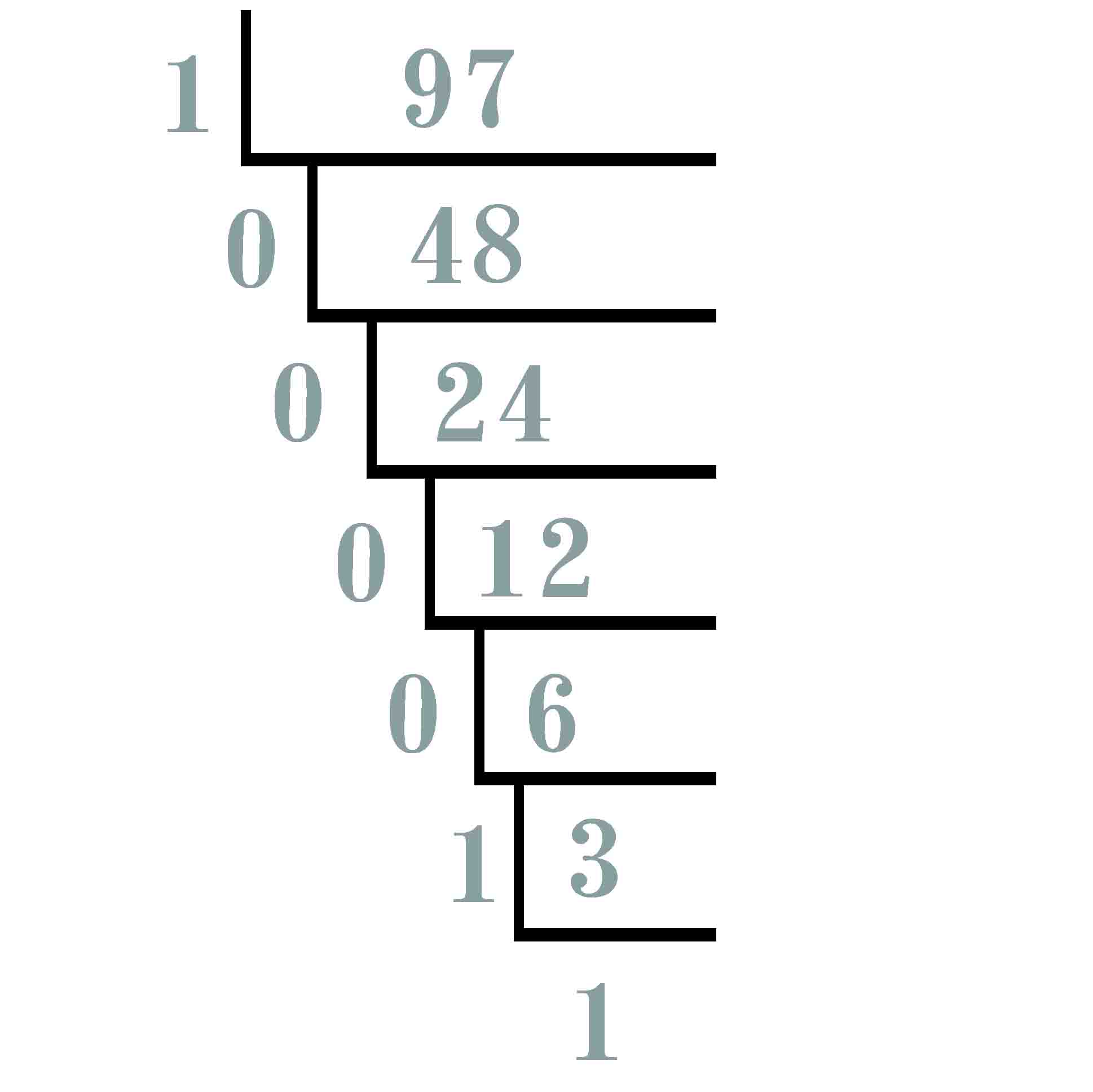
将所得余数从下往上依次列出即为97的二进制数，是1100001（2）。

二进制——十进制

计算公式：a*2⁰+b*2¹+c*2²+d*2³+~+n*2^n-1=

例1001100=0*2⁰+0*2¹+1*2²+1*2³+~+1*2⁶=76（2）

十进制——八进制

十进制数逐次整除8，直至商为0所得余数按照相反的顺序写出，即为八进制数。

例963的八进制数

将所得余数从下往上依次列出即为963的八进制数，是1703（8）。

八进制——十进制

计算公式：a*8⁰+b*8¹+c*8²+d*8³+~+n*8^n-1=

例：1643=3*8⁰+4*8¹+6*8²+1*8³=931（8）

十进制——十六进制

十进制除以十六，0—9，（10）A，（11）B，（12）C，（13）D，（14）E，（15）F

十进制数逐次整除16，直至商为0，所得余数按照相反的顺序写出，即为十六进制数。

例：7921的十六进制数

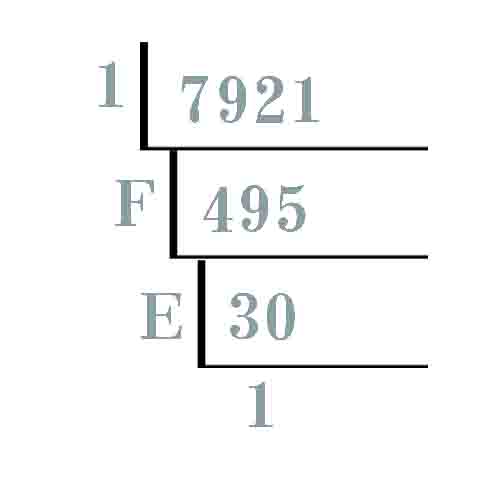
将所得余数从下往上依次列出即为7921的十六进制数，是1EF1（16）。

十六进制——十进制

计算公式：a*16⁰+b*16¹+c*16²+d*16³+~+n*16^n-1=

例：32FA=A（10）*16⁰+F（15）*16¹+2*16²+3*16³=13050（16）

其他进制之间的转化

二进制——八进制

对于整数，采用从右到左每三位一组，不够三位的在其左边补齐0，每组单独转换出来，即为八进制数。

例：1001010011的八进制数

（001     001       010       011）

    1         1           2           3  

所以，（1123）即为所得的八进制数。

八进制——二进制

将每位八进制由三位二进制数代替，即可完成转换。

例：1735（8）的二进制数

十进制数	1	2	4	8
公式原型	20	21	22	23

5=1+4=2⁰+2²

依次倒着写，所以5是101。

3是011,7是111,1是001。

1735（8）的二进制数是1111011101（2）。

二进制——十六进制

由于2的4次方=16，所以依照二进制与八进制的转换方法，将二进制数的每四位用一个十六进制数码来表示，整数部分以小数点为界点从右往左每四位一组转换，小数部分从小数点开始自左向右每四位一组进行转换。

例：（1001      0110     0101    1110  ）

       9             6           5          E

十六进制——二进制

只要将每一位十六进制数用四位相应的二进制数表示，即可完成转换。

例：EBDF(16)的二进制数

F=15=2⁰+2²+2³+2⁴

依次倒着写，所以F是1111。

D是1101，B是1011，E是1110

EBDF（16）的二进制数是1110101111011111（2）。